人口增長模型

来源:https://www.cnblogs.com/hznudmh/archive/2022/06/15/16343159.html
-Advertisement-
Play Games

1. 指數增長模型 設第今年的人口為 \(x_0\)，年增長率為 \(r\)，預測 \(k\) 年後的人口為 \(x_k\)，則有 \[ x_k = x_0(1+r)^k \tag{1} \] 這個模型的前提是年增長率 \(r\) 在 \(k\) 年內保持不變. 利用 (1) 式可以根據人口估計年增 ...


目錄

1. 指數增長模型

設第今年的人口為 \(x_0\)，年增長率為 \(r\)，預測 \(k\) 年後的人口為 \(x_k\)，則有

\[x_k = x_0(1+r)^k \tag{1} \]

這個模型的前提是年增長率 \(r\) 在 \(k\) 年內保持不變.

利用 (1) 式可以根據人口估計年增長率，例如經過 \(n\) 年後人口翻了一番，那麼這期間的年平均增長率約為 \((70/n)\%\).
證明：

\[\begin{aligned} &x_n = x_0(1+r)^n \Longrightarrow 2x_0 = x_0(1+r)^n \Longrightarrow (1+r)^n = 2 \Longrightarrow \ln(1+r)=\frac{\ln 2}{n}\\ \Longrightarrow & 1+r=e^{\frac{\ln 2}{n}} \Longrightarrow r = e^{\frac{\ln2}{n}}-1 \sim \frac{\ln2}{n} \approx (\frac{70}{n})\% \end{aligned} \]

1.1 人口增長模型的建立

將人口看作連續時間 \(t\) 的連續可微函數 \(x(t)\). 於是有

\[\frac{\mathrm{d}x}{\mathrm{d}t} = rx,\quad x(0) = x_0 \tag{2} \]

求解上述微分方程：

\[\begin{aligned} &原式 \ = \frac{1}{x}\mathrm{d}x = r\mathrm{d}t\\ \\ \Longrightarrow & \ln x = rt+C\\ \\ \Longrightarrow & x = e^{rt}\cdot C\\ \end{aligned} \]

由於 \(x(0) = x_0\)，代入上式可得 \(x_0 = C\)，可以解出

\[x(t) = x_0e^{rt} \tag{3} \]

可以用 R 語言定義指數增長模型方程

## 指數增長模型方程
fun1 <- function(t) x0 * exp(r*t)

1.2 參數估計

以書本 P142 美國人口數據為例

1.1.1 線性最小二乘估計

對 (3) 取對數，有 \(\ln x = \ln x_0 + rt\)，於是 \(\ln x\) 與 \(t\) 存線上性關係，令10年為一個單位.
下麵用 R 進行參數估計.

> ## 美國人口數據的導入
> x <- c(3.9, 5.3, 7.2, 9.6, 12.9, 17.1, 23.2, 31.4,
+        38.6, 50.2, 62.9, 76.0, 92.0, 105.7, 122.8,
+        131.7, 150.7, 179.3, 203.2, 226.5, 248.7, 281.4)
> ## 線性最小二乘估計
> y <- log(x)
> t <- sequence(length(x), 0, 1)
> lm(y~t) -> sol
> summary(sol)

Call:
lm(formula = y ~ t)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.43901 -0.19764  0.00609  0.23405  0.32145 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.79999    0.10538   17.08 2.14e-13 ***
t            0.20201    0.00859   23.52 4.80e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.2556 on 20 degrees of freedom
Multiple R-squared:  0.9651,	Adjusted R-squared:  0.9634 
F-statistic: 553.1 on 1 and 20 DF,  p-value: 4.8e-16
> exp(1.79999)
[1] 6.049587

結果分析：

\[\ln x = 0.2020t + 1.79999 \]

於是\(r = 0.2020/10年, \ x_0 = e^{1.79999}=6.0496\)

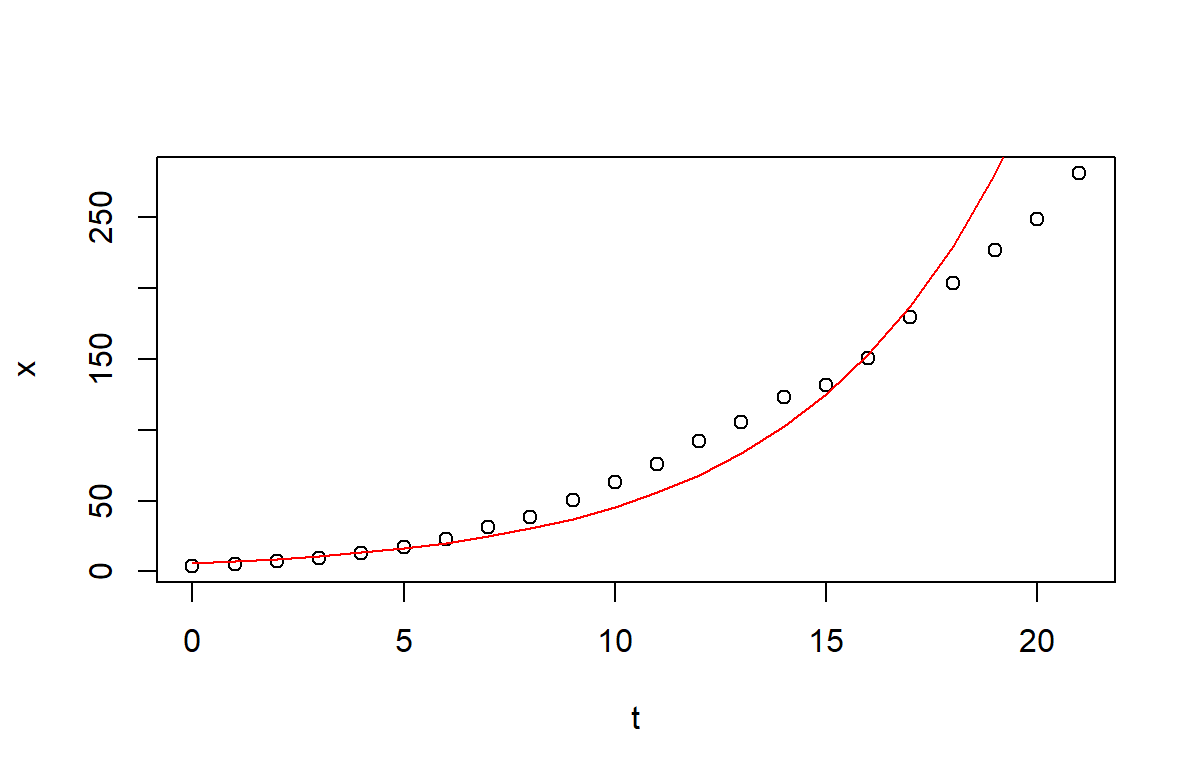
通過圖像看看擬合效果：

# 擬合圖像
x0 <- exp(1.79999)
r <- 0.20201
y_hat1 <- fun1(t)
plot(t, x)
lines(t, y_hat1, col="red")

1.1.2 基於數值微分的參數估計

對人口數據作數值微分，進而計算增長率，將增長率的平均值作為 \(r\) 的估計；\(x_0\) 直接採用原始數據.
理論依據：

\[\frac{\mathrm{d }x}{\mathrm{d}t} = rx \Longrightarrow \frac{\mathrm{d}x/\mathrm{d}t}{x} = r \]

數值微分可用中點公式算近似值：

\[x'(t_k) = \frac{x_{k+1}-x_{k-1}}{2\Delta t}, \ k = 1, 2, \cdots, n-1\\ x'(t_0) = \frac{-3x_0+4x_1-x_2}{2\Delta t}, \ x'(t_n) = \frac{x_{n-2}-4x_{n-1}+3x_n}{2\Delta t} \]

下麵用 R 語言計得出 \(r\) 的估計值

> ## 數值微分估計
> dx <- c()
> dx[1] <- (-3*x[1]+4*x[2]-x[3])/2 # 數值微分中點公式的應用
> for (i in 2:(length(x)-1)){
+   dx[i] <- (x[i+1]-x[i-1])/2 # 數值微分中點公式的應用
+ }
> dx[length(x)] <- (x[length(x)-2]-4*x[length(x)-1]+3*x[length(x)])/2 # 數值微分中點公式的應用
> R <- dx/x # 增長率序列
> r <- mean(R) # 其平均值就是r的估計
> r
[1] 0.02051861

通過圖像看看擬合效果

# 擬合圖像
x0 <- x[1]
y_hat2 <- fun1(t)
plot(t, x)
lines(t, y_hat2, col="red")

1.3 改進的指數增長模型

在前面的模型中，我們假定了每年人口的增長率是固定的，顯然這是存在缺陷的，每年的增長率應是時間的函數，即增長率為 \(r(t)\).

我們首先畫出 \(r(t)\) 與 \(t\) 的散點圖（這裡我們的增長率用的是1.2.2中做數值微分得到的增長率序列），看看他們存在什麼函數關係

## 畫出 r~t 散點圖
plot(t,R)

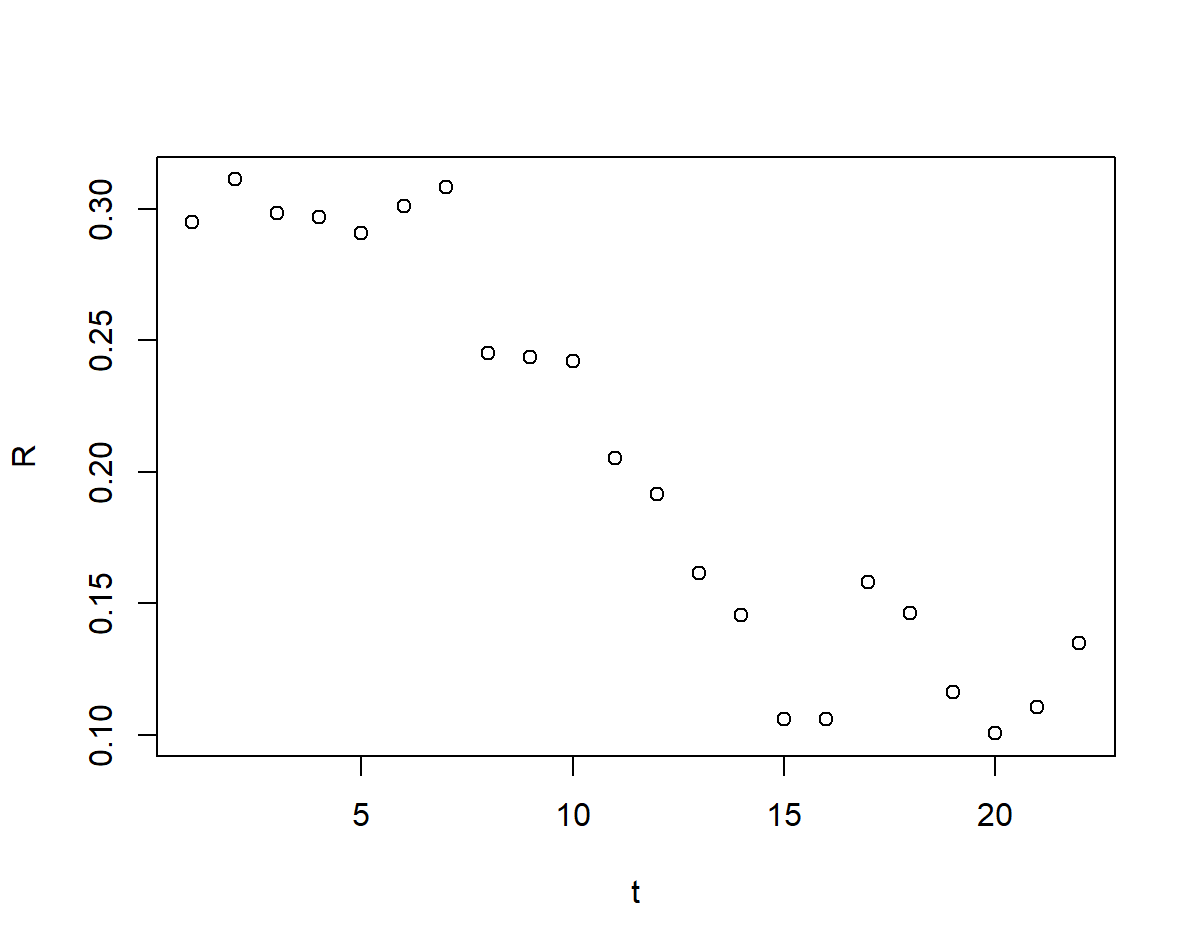
可以看出兩者疑似存線上性關係，不妨做線性擬合

> ## 線性擬合
> lm(R~t) -> sol2
> summary(sol2)

Call:
lm(formula = R ~ t)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.059303 -0.007904 -0.001237  0.015108  0.051549 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.3252461  0.0117048   27.79  < 2e-16 ***
t           -0.0114343  0.0009541  -11.98 1.39e-10 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.02839 on 20 degrees of freedom
Multiple R-squared:  0.8778,	Adjusted R-squared:  0.8717 
F-statistic: 143.6 on 1 and 20 DF,  p-value: 1.391e-10

結果分析：

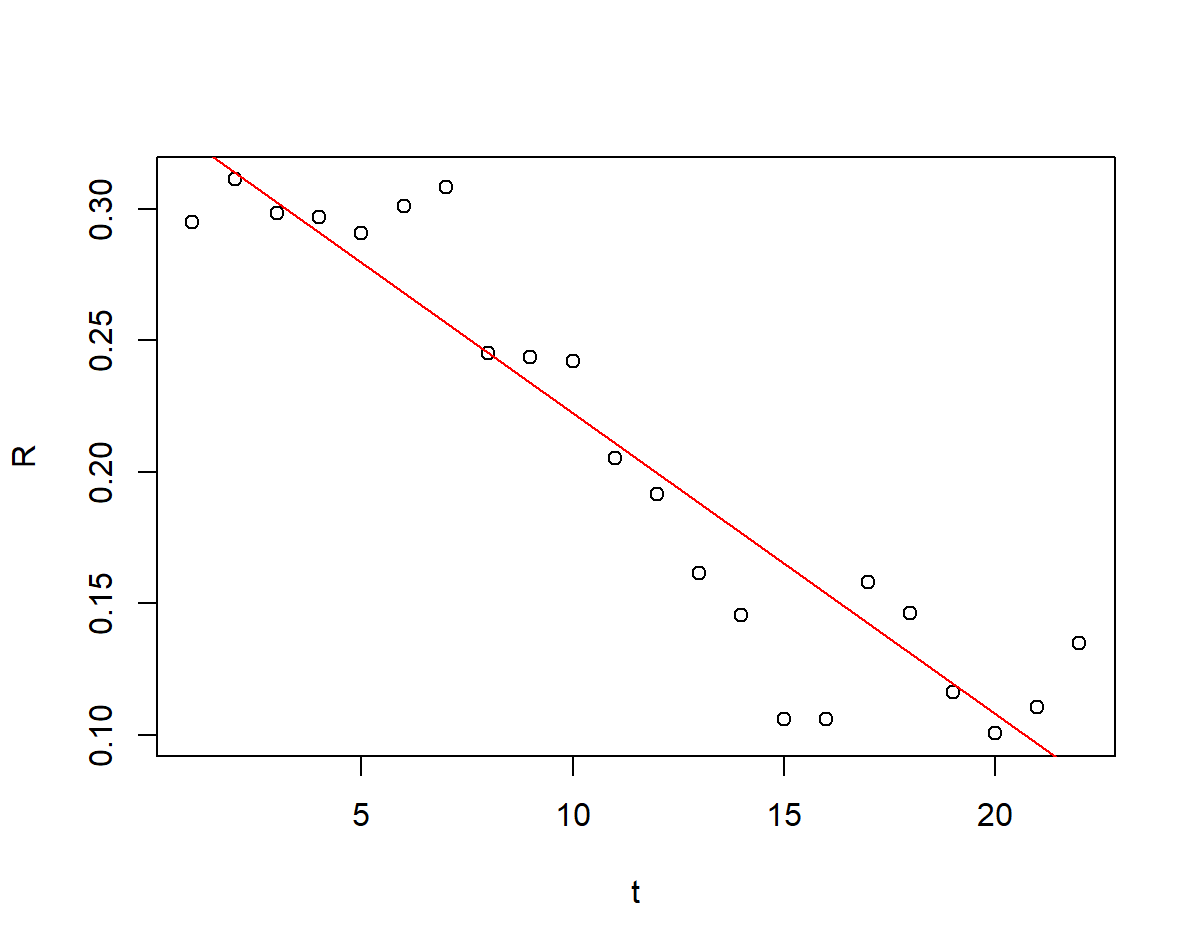
\[r = 0.3252461 - 0.0114343t \]

且回歸方程的檢驗統計量\(F=143.6, \ p = 1.391e-10 << 0.01, \ R^2 = 0.8778\)，認為回歸方程的擬合程度不錯，兩者存在非常顯著的線性關係；常數項檢驗 \(t = 27.79, \ p << 0.01\)，一次項繫數檢驗 \(t = -11.98, \ p = 1.39e-10 << 0.01\)，認為回歸方程繫數顯著不為0.

看看擬合圖像

# 擬合圖像
plot(t,R)
abline(sol2, col = "red")

記 \(r = r_0 - r_1t\)，於是 \((2)\) 式變為

\[\frac{\mathrm{d}x}{\mathrm{d}t} = (r_0-r_1t)x, \quad x(0) = x_0 \tag{4} \]

用分離變數的方法求解上述微分方程，\((4)\) 可化為

\[\begin{aligned} &\frac{1}{x}\mathrm{d}x = (r_0-r_1t)\mathrm{d}t\\ \Longrightarrow &\int \frac{1}{x}\mathrm{d}x = \int (r_0-r_1t)\mathrm{d}t\\ \Longrightarrow &\ln x = r_0-\frac{1}{2}r_1t^2 + C\\ \Longrightarrow &x = C'\exp(r_0t-\frac{1}{2}r_1t^2)\\ \end{aligned} \]

將 \(x(0) = x_0\) 代入，即可得 \(C' = x_0\)，於是解得

\[x(t) = x_0\exp(r_0t-\frac{1}{2}r_1t^2) \]

可以用 \(R\) 語言定義上述函數

## 定義函數
fun2 <- function(t) x0 * exp(r0*t - r1*t^2/2)

下麵用 \(R\) 語言做指數增長模型的擬合

## 利用模型估計人口並做擬合圖像
r0 <- 0.3252461
r1 <- 0.0114343
x0 <- x[1]
t <- sequence(length(x), 0, 1)
y_hat3 <- fun2(t)
plot(t, x)
lines(t, y_hat3, col = "red")

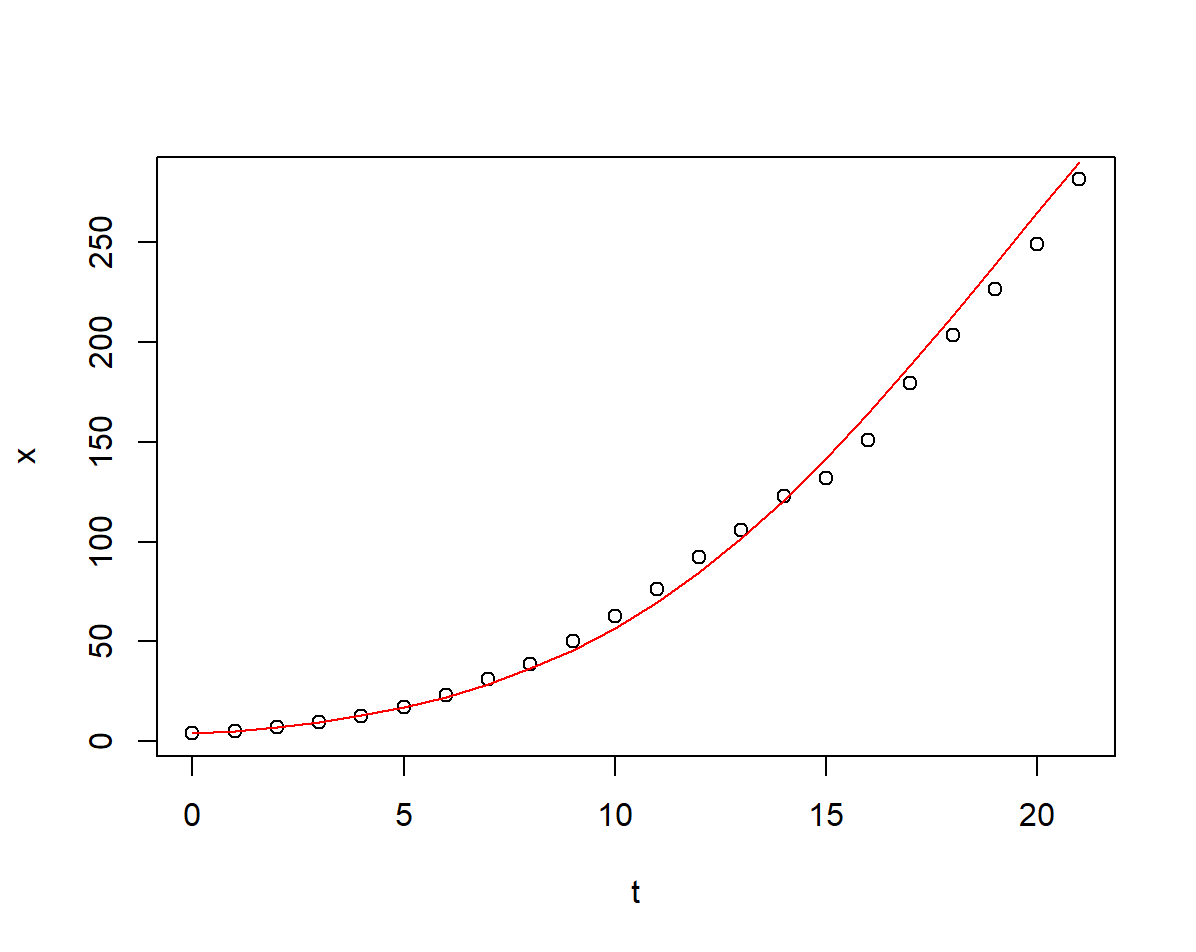
可以看出改進的指數增長模型的擬合程度明顯好於改進前的指數增長模型.

2. logistic 模型

考慮自然資源、環境條件等因素對人口增長起阻礙作用，並且隨著人口的增加，阻礙作用越來越大.

2.1 logistic 模型的建立

隨著人口的增長，資源和環境的阻礙作用體現在對增長率 \(r\) 的影響上，於是 \(r(x)\) 是 \(x\) 的函數，主觀上我們認為 \(r(x)\) 是減函數，我們可以畫出兩者之間的散點圖來大致判斷兩者之間滿足何種函數關係（這裡我們的增長率用的是1.2.2中做數值微分得到的增長率序列）

## r~x 散點圖
plot(x, R)

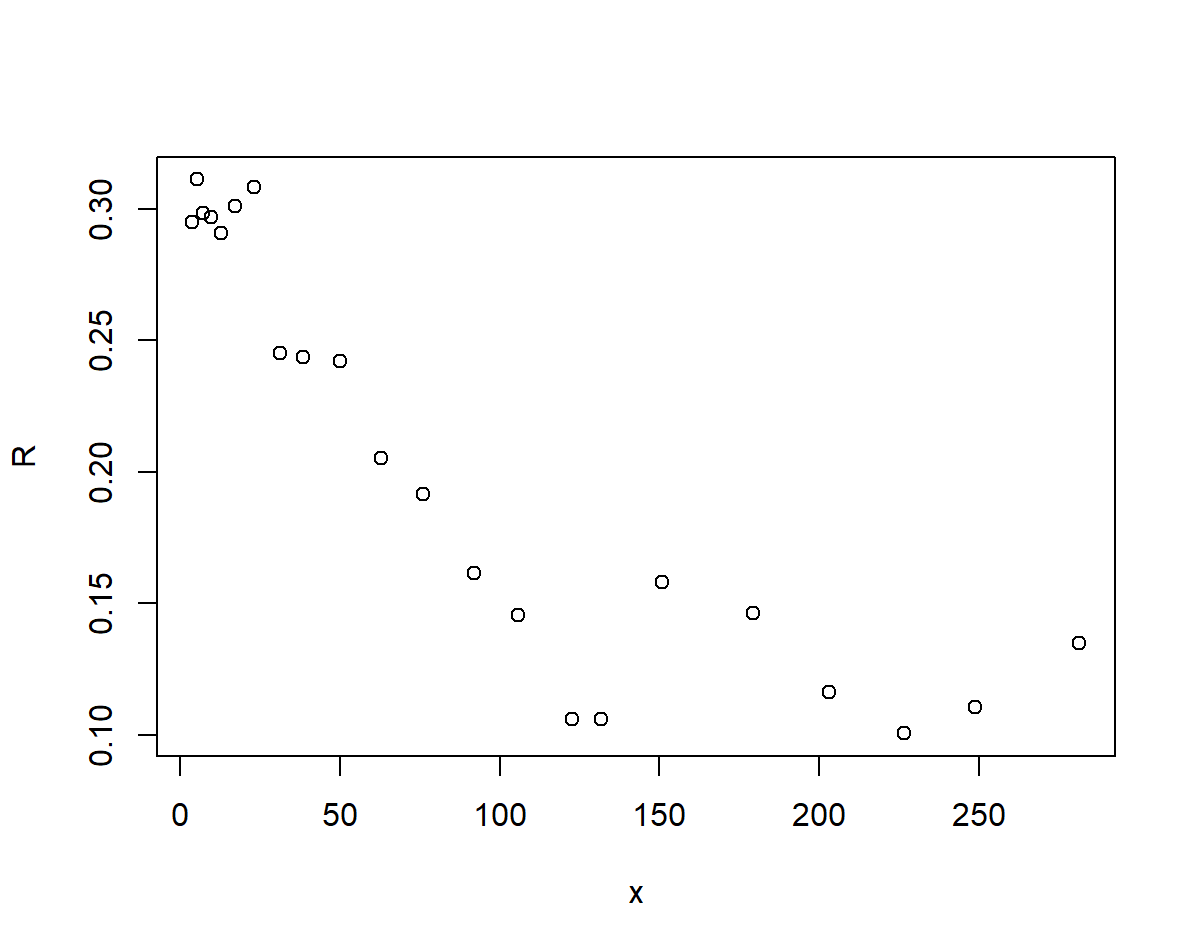
散點圖顯示兩者之間存線上性關係，不妨設 \(r(x) = a + bx\)，為了賦予繫數 \(a,b\) 實際含義，引入兩個參數：

  • 內稟增長率 \(r_0\) \(\quad r_0\) 是 \(x=0\) 的增長率，於是 \(a = r_0\);
  • 人口容量 \(x_m\) \(\quad x_m\) 是資源和環境所能容納的最大人口數量，也就是當 \(x=x_m\) 後人口不再增長，即 \(r(x_m) = r + bx_m = 0\)，解得 \(b = -\frac{r}{x_m}\).

於是

\[r(x) = r_0(1-\frac{x}{x_m}) \]

那麼 \((2)\) 變為

\[\frac{\mathrm{d}x}{\mathrm{d}t} = r_0x(1-\frac{x}{x_m}), \quad x(0) = x_0 \tag{5} \]

上式稱為 logistic 方程.

將上式化為

\[\begin{aligned} &\frac{x_m}{x(x_m-x)} \mathrm{d}x = r\mathrm{d}t\\ \Longrightarrow &\int(\frac{1}{x} + \frac{1}{x_m-x})\mathrm{d}x = \int r_0\mathrm{d}t\\ \Longrightarrow &\ln{x} - \ln{(x_m-x)} = r_0t + C\\ \Longrightarrow &\frac{x}{x_m-x}=C'e^{r_0t}\\ \Longrightarrow &x = \frac{x_m}{1+C''e^{-r_0t}}\\ \end{aligned} \]

將點 \((t,x) = (0,x_0)\) 代入上式可得

\[C'' = \frac{x_m}{x_0}-1 \]

綜上就可求得

\[x(t) = \frac{x_m}{1+(\frac{x_m}{x_0}-1)e^{-r_0t}} \tag{6} \]

上式稱為 logistic 曲線. \((5),(6)\) 統稱為 logistic 模型.

利用 R 語言定義上述函數

## 定義函數
fun3 <- function(t) xm/(1+(xm/x0-1)*exp(-r0*t))

2.2 參數估計

2.2.1 線性最小二乘估計

\((5)\) 式可改寫為

\[\frac{\mathrm{d}x/\mathrm{d}t}{x} = r_0 - \frac{r_0}{x_m}x, \quad x(0) = x_0 \]

下麵用 R 語言做線性估計

> ## 線性最小二乘估計
> lm(R~x) -> sol3
> summary(sol3)

Call:
lm(formula = R ~ x)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.076819 -0.021568  0.000946  0.023945  0.078560 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  2.805e-01  1.243e-02  22.573 1.06e-15 ***
x           -7.968e-04  9.763e-05  -8.162 8.55e-08 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.03902 on 20 degrees of freedom
Multiple R-squared:  0.7691,	Adjusted R-squared:  0.7575 
F-statistic: 66.61 on 1 and 20 DF,  p-value: 8.546e-08

結果分析：

\[\frac{\mathrm{d}x/\mathrm{d}t}{x} = 0.2805 - 7.968e-04 x \]

且回歸方程的檢驗統計量\(F=66.61, \ p = 8.546e-08 << 0.01, \ R^2 = 0.7691\)，認為回歸方程的擬合程度不錯，兩者存在非常顯著的線性關係；常數項檢驗 \(t = 22.573, \ p << 0.01\)，一次項繫數檢驗 \(t = -8.162, \ p << 0.01\)，認為回歸方程繫數顯著不為0.

於是 \(r_0 = 0.2805, \ x_m = 0.1805/7.968e-04 = 352.0331\)，畫出擬合圖像

# 擬合
r0 = 0.2805
xm = 0.2805/7.968e-04
y_hat4 <- fun3(t)
plot(t, x)
lines(t, y_hat4, col = "red")

2.2.2 非線性最小二乘法

考慮 Levenberg-Marquadt 方法求解，\((6)\) 式可化為

\[x(t) - \frac{x_m}{1+(\frac{x_m}{x_0}-1)e^{-r_0t}} = 0 \]

帶估計參數為 \((x_m,x_0,r_0)\)，給定初始值 \((400,4,0.25)\)，用 R 求解

> ## 非線性最小二乘估計
> library(pracma)
> fun4 <- function(z) {
+   f <- numeric(22)
+   for (i in 1:22){
+     f[i] <- x[i] - z[1]/(1+(z[1]/z[2]-1)*exp(-z[3]*(i-1)))
+   }
+   f
+ }
> sol4 <- lsqnonlin(fun4, x0 = c(400,4,0.25))
> sol4
$x
[1] 443.9948201   7.6962896   0.2154783

$ssq
[1] 458.2113

$ng
[1] 0.0002470027

$nh
[1] 3.847784e-06

$mu
[1] 7.431693e-06

$neval
[1] 22

$errno
[1] 1

$errmess
[1] "Stopped by small x-step."

於是可得參數的估計值為 \(x_m = 443.9948201, \ x_0 = 7.6962896, \ r_0 = 0.2154783\).

下麵將估計的參數代入 \((6)\)，得出擬合圖像

# 擬合
xm = 443.9948201
x0 = 7.6962896
r0 = 0.2154783
y_hat5 <- fun3(t)
plot(t, x)
lines(t, y_hat5, col = "red")

2.3 比較

為了比較線性最小二乘估計和非線性最小二乘估計的擬合程度，引入均方誤差，均方誤差越小說明擬合程度越高

\[MSE = \frac{1}{n}\sum_{i=1}^n(x_i-\hat{x}_i)^2 \]

下麵用 R 計算兩種方法的均方誤差

> ## 比較
> MSE1 <- sum((y_hat4-x)^2)/length(x)
> MSE2 <- sum((y_hat5-x)^2)/length(x)
> print(MSE1)
[1] 127.1399
> print(MSE2)
[1] 20.82779

發現 \(MS1 = 127.1399 > 20.82779 = MSE2\)，因此非線性最小二乘參數估計的擬合效果更好.

不妨再計算一下改進的指數增長模型的均方誤差

> MSE3 <- sum((y_hat3-x)^2)/length(x)
> MSE3
[1] 51.51463

可以發現，logistic模型的非線性最小二乘估計參數的結果要好於改進的指數增長模型.


您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • tree-shaking
    來源 tree-shaking 最早由 Rich Harris 在 rollup 中提出。 為了減少最終構建體積而誕生。 以下是 MDN 中的說明： tree-shaking 是一個通常用於描述移除 JavaScript 上下文中的未引用代碼(dead-code) 行為的術語。 它依賴於 ES201 ...
  • 【ES6】迭代器
    簡介 在 JavaScript 中，迭代器是一個對象，它定義一個序列，併在終止時可能返回一個返回值。 更具體地說，迭代器是通過使用 next() 方法實現迭代器協議的任何一個對象，該方法返回具有兩個屬性的對象： value，這是序列中的 next 值；和 done ，如果已經迭代到序列中的最後一個值 ...
  • node前後端交互（Express）
    1. Express框架是什麼 1.1 Express是一個基於Node平臺的web應用開發框架，它提供了一系列的強大特性，幫助你創建各種Web應用。我們可以使用 npm install express 命令進行下載。 1.2 Express初體驗 // 引入express框架 const expr ...
  • Java遞歸查找層級文件夾下特定內容的文件
    遞歸查找文件 引言 或許是文件太多,想找某個文件又忘記放哪了;又或者是項目改造,需要將外部調用介面進行改造,項目太多,又無法排查。那麼怎麼快速找到自己想要的內容就是一件值得思考的事情了。 根據特定內容尋找文件位置 package com.lizi.globalexception.Utils; imp ...
  • MyBatis流式查詢
    大家好，本文我將繼續來剖析SpringCloud中負載均衡組件Ribbon的源碼。本來我是打算接著OpenFeign動態代理生成文章直接講Feign是如何整合Ribbon的，但是文章寫了一半發現，如果不把Ribbon好好講清楚，那麼有些Ribbon的細節理解起來就很困難，所以我還是打算單獨寫一篇文章 ...
  • phpcurl函數類模擬Curl get post header refer攜帶Cookie模擬訪問來源Refer模擬UseaAgent
    phpcurl函數類模擬Curl get post header refer攜帶Cookie模擬訪問來源Refer模擬UseaAgent ...
  • SpringBoot集成feign的方法分享
    一個工作5年的粉絲找到我，他說參加美團面試，遇到一個基礎題沒回答上來。 這個問題是：“資料庫連接池有什麼用？以及它有哪些關鍵參數”？ 我說，這個問題都不知道，那你項目裡面的連接池配置怎麼設置的？ 你們猜他怎麼回答。懂得懂得啊。 好的，關於這個問題，我們來看看普通人和高手的回答。 普通人： 資料庫連接 ...
  • 流量管制-令牌桶與漏桶
    Principle of token bucket 隨著互聯網的發展，在處理流量的方法也不僅僅為 first-come，first-served，而在共用網路中實現流量管理的基本機制就是排隊。而公平演算法則是實現在優先順序隊列中基於哪些策略來排隊的”公平隊列“。Token Bucket 則是為公平排隊提 ...
一周排行
    -Advertisement-
    Play Games
  • C#TMS系統學習（BaseCity頁面）
    C#TMS系統代碼-基礎頁面BaseCity學習 本人純新手，剛進公司跟領導報道，我說我是java全棧，他問我會不會C#，我說大學學過，他說這個TMS系統就給你來管了。外包已經把代碼給我了，這幾天先把增刪改查的代碼背一下，說不定後面就要趕鴨子上架了 Service頁面 //using => impo ...
  • C# - 委托與事件
    委托與事件 委托 委托的定義 委托是C#中的一種類型，用於存儲對方法的引用。它允許將方法作為參數傳遞給其他方法，實現回調、事件處理和動態調用等功能。通俗來講，就是委托包含方法的記憶體地址，方法匹配與委托相同的簽名，因此通過使用正確的參數類型來調用方法。 委托的特性 引用方法：委托允許存儲對方法的引用， ...
  • 解析 ABP vNext 依賴註入實現【屬性註入】的原理
    前言 這幾天閑來沒事看看ABP vNext的文檔和源碼，關於關於依賴註入(屬性註入)這塊兒產生了興趣。 我們都知道。Volo.ABP 依賴註入容器使用了第三方組件Autofac實現的。有三種註入方式，構造函數註入和方法註入和屬性註入。 ABP的屬性註入原則參考如下： 這時候我就開始疑惑了，因為我知道 ...
  • C#TMS系統學習（ShippingNotice頁面）
    C#TMS系統代碼-業務頁面ShippingNotice學習 學一個業務頁面，ok，領導開完會就被裁掉了，很突然啊，他收拾東西的時候我還以為他要旅游提前請假了，還在尋思為什麼回家連自己買的幾箱飲料都要叫跑腿帶走，怕被偷嗎？還好我在他開會之前拿了兩瓶芬達 感覺感覺前面的BaseCity差不太多，這邊的 ...
  • C#動態查詢：巧用Expression組合多條件表達式
    概述：在C#中，通過`Expression`類、`AndAlso`和`OrElse`方法可組合兩個`Expression<Func<T, bool>>`，實現多條件動態查詢。通過創建表達式樹，可輕鬆構建複雜的查詢條件。 在C#中，可以使用AndAlso和OrElse方法組合兩個Expression< ...
  • 在Biwen.QuickApi中整合一個極簡的發佈訂閱(事件匯流排)
    閑來無聊在我的Biwen.QuickApi中實現一下極簡的事件匯流排,其實代碼還是蠻簡單的,對於初學者可能有些幫助 就貼出來,有什麼不足的地方也歡迎板磚交流~ 首先定義一個事件約定的空介面 public interface IEvent{} 然後定義事件訂閱者介面 public interface I ...
  • WPF 穩定的全屏化視窗方法
    1. 案例 成某三甲醫預約系統， 該項目在2024年初進行上線測試，在正常運行了兩天後，業務系統報錯：The connection pool has been exhausted, either raise MaxPoolSize (currently 800) or Timeout (curren ...
  • 在 WPF 中集成 ASP.NET Core 和 WebView2 用於集成 SPA 應用
    背景 我們有些工具在 Web 版中已經有了很好的實踐，而在 WPF 中重新開發也是一種費時費力的操作，那麼直接集成則是最省事省力的方法了。 思路解釋 為什麼要使用 WPF？莫問為什麼，老 C# 開發的堅持，另外因為 Windows 上已經裝了 Webview2/edge 整體打包比 electron ...
  • C#事件
    EDP是一套集組織架構，許可權框架【功能許可權，操作許可權，數據訪問許可權，WebApi許可權】，自動化日誌，動態Interface，WebApi管理等基礎功能於一體的，基於.net的企業應用開發框架。通過友好的編碼方式實現數據行、列許可權的管控。 ...
  • .Net8.0 Blazor Hybird 桌面端 (WPF/Winform) 發佈到 Win7+
    .Net8.0 Blazor Hybird 桌面端 (WPF/Winform) 實測可以完整運行在 win7sp1/win10/win11. 如果用其他工具打包,還可以運行在mac/linux下, 傳送門BlazorHybrid 發佈為無依賴包方式 安裝 WebView2Runtime 1.57 M ...
所有分類