本章是系列文章的第三章,介紹了基於數據流分析的一些優化方法。包括生命周期管理,可獲得表達式,常用表達式,可達性定義。本章在介紹這4中分析方法的基礎上提取出它們的通用模式。這一章形式化的內容比較多,看的時候有點燒腦,最好自己手工推導一下,要不然基本上看不懂:) 本文中的所有內容來自學習DCC888的學 ...
本章是系列文章的第三章,介紹了基於數據流分析的一些優化方法。包括生命周期管理,可獲得表達式,常用表達式,可達性定義。本章在介紹這4中分析方法的基礎上提取出它們的通用模式。這一章形式化的內容比較多,看的時候有點燒腦,最好自己手工推導一下,要不然基本上看不懂:)
本文中的所有內容來自學習DCC888的學習筆記或者自己理解的整理,如需轉載請註明出處。周榮華@燧原科技
3.1 生命周期
對下麵的程式:
1 var x,y,z; 2 x = input; 3 while (x > 1) { 4 y = x / 2; 5 if (y > 3) 6 x = x - y; 7 z = x - 4; 8 if (z > 0) 9 x = x / 2; 10 z = z - 1; 11 } 12 output x;
可以生成控制流圖如下:

圖對應dot文件內容:
1 digraph "CFG for 3.1"{ 2 rankdir=LR 3 "var x,y,z" -> "x = input" -> "x > 1" -> {"output x" "y = x / 2"} 4 "y = x / 2" -> "y > 3" -> {"x = x - y" "z = x - 4"} 5 "x = x - y" -> "z = x - 4" -> "z > 0" -> {"x = x / 2" "z = z - 1"} 6 "x = x / 2" -> "z = z - 1" -> "x > 1"
但僅有控制流分析,還有很多問題無法解決。第一個問題是電腦需要知道這個程式需要多少寄存器,甚至需要控制流執行到某條邊的時候,需要多少個寄存器?有什麼通用的方法能用來回答這個問題?
活躍變數:如果程式在執行點需要使用某個變數,並且該使用不是定義類的使用,那麼程式需要在緊靠該執行點之前就要能訪問這個變數,這種變數稱為活躍變數(alive)。
對每個程式執行點p,我們定義2個集合:
- IN是在緊靠p之前活著的變數集合。
- OUT是在緊靠p之後或者的變數集合。
活躍變數的數據流等式:
對 p : v = E
IN(p) = ( OUT(p) \ {v} ) ∪ vars(E)
OUT(p) = ∪ IN(ps), ps ∈ succ(p)
IN(p) :p之前的活躍的變數集合
OUT(p) :p之後的活躍的變數集合
vars(E) :表達式E中出現的所有變數的集合
succ(p) :控制流圖中p的所有後繼的集合
對CFG上的每個點,變數上面2個等式,直到2個集合不再變化,我們就得到了任意點的變數生命周期。
這個等式最早是Albeit用prolog實現的:
1 diff([], _, []). 2 diff([H|T], L, LL) :- member(H, L), diff(T, L, LL). 3 diff([H|T], L, [H|LL]) 4 :- \+member(H, L), diff(T, L, LL). 5 union([], L, L). 6 union([H|T], L, LL) :- member(H, L), union(T, L, LL). 7 union([H|T], L, [H|LL]) 8 :- \+ member(H, L), union(T, L, LL). 9 in(1, L) :- out(1, Out), diff(Out, [y], L). 10 in(2, L) :- out(2, Out), diff(Out, [x], L). 11 in(3, L) :- out(3, Out), diff(Out, [z], Diff), 12 union(Diff, [x, y], L). 13 in(4, L) :- out(4, Out), union(Out, [z], L). 14 out(1, L) :- in(2, L). 15 out(2, L) :- in(3, L). 16 out(3, L) :- in(4, L). 17 out(4, []).
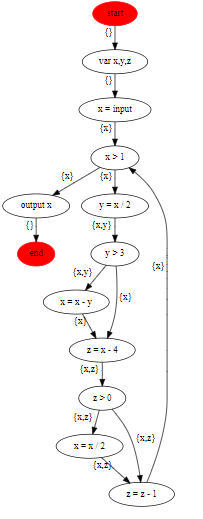
上面的控制流圖,給每條邊加上變數的生命周期之後的結果的dot表達是這樣的:
1 digraph "CFG for 3.2"{ 2 "start" [bgcolor=black color=red style=filled] 3 "start" -> "var x,y,z" [xlabel="{}"] 4 "var x,y,z" -> "x = input" [xlabel="{}"] 5 "x = input" -> "x > 1" [xlabel="{x}"] 6 "x > 1" -> "output x" [xlabel="{x}"] 7 "x > 1" -> "y = x / 2" [xlabel="{x}"] 8 "y = x / 2" -> "y > 3" [xlabel="{x,y}"] 9 "y > 3" -> "x = x - y" [xlabel="{x,y}"] 10 "y > 3" -> "z = x - 4" [xlabel="{x}"] 11 "x = x - y" -> "z = x - 4" [xlabel="{x}"] 12 "z = x - 4" -> "z > 0" [xlabel="{x,z}"] 13 "z > 0" -> "x = x / 2" [xlabel="{x,z}"] 14 "z > 0" -> "z = z - 1" [xlabel="{x,z}"] 15 "x = x / 2" -> "z = z - 1" [xlabel="{x,z}"] 16 "z = z - 1" -> "x > 1" [xlabel="{x}"] 17 "output x" -> "end" [xlabel="{}"] 18 "end" [bgcolor=black color=red style=filled] 19 }
dot文件生成的svg圖是這樣的:
3.2 可訪問表達式(Available Expressions)
可訪問表達式:一個表達式E在程式點p是可訪問表達式,當且僅當:
-
- E在p之前是可訪問表達式,
- 並且E的任意一個變數在p未重新定義;
或者:
-
- E在p處被使用,
- E的所有變數沒有在p處重新定義。
可訪問表達式的數據流等式:
對 p : v = E
IN(p) = ∩OUT(ps), ps ∈ pred(p)
OUT(p) = ( IN(p) ∪ {E}) \ {Expr(v)}
IN(p) :p之前的可訪問表達式集合
OUT(p) :p之後的可訪問表達式集合
pred(p) :控制流圖中p的所有前驅的集合
Expr(v) :使用變數v的所有表達式的集合
可訪問表達式的例子:

3.3 常用表達式(Very Busy Expressions)
常用表達式:當表達式E從p開始到程式結束前的每條路徑上都會計算,則稱表達式E在p處是常用表達式。形式化描述就是:
-
- E在p之後是常用表達式,
- 並且E的所有變數並沒有在p處重新定義;
或者:
-
- p處使用了表達式E。
常用表達式的數據流等式:
對 p : v = E
IN(p) = ( OUT(p) \ {Expr(v)}) ∪ {E}
OUT(p) = ∩ IN(ps), ps ∈ succ(p)
IN(p) :p之前的常用表達式集合
OUT(p) :p之後的常用表達式集合
succ(p) :控制流圖中p的所有後繼的集合
常用表達式的例子:
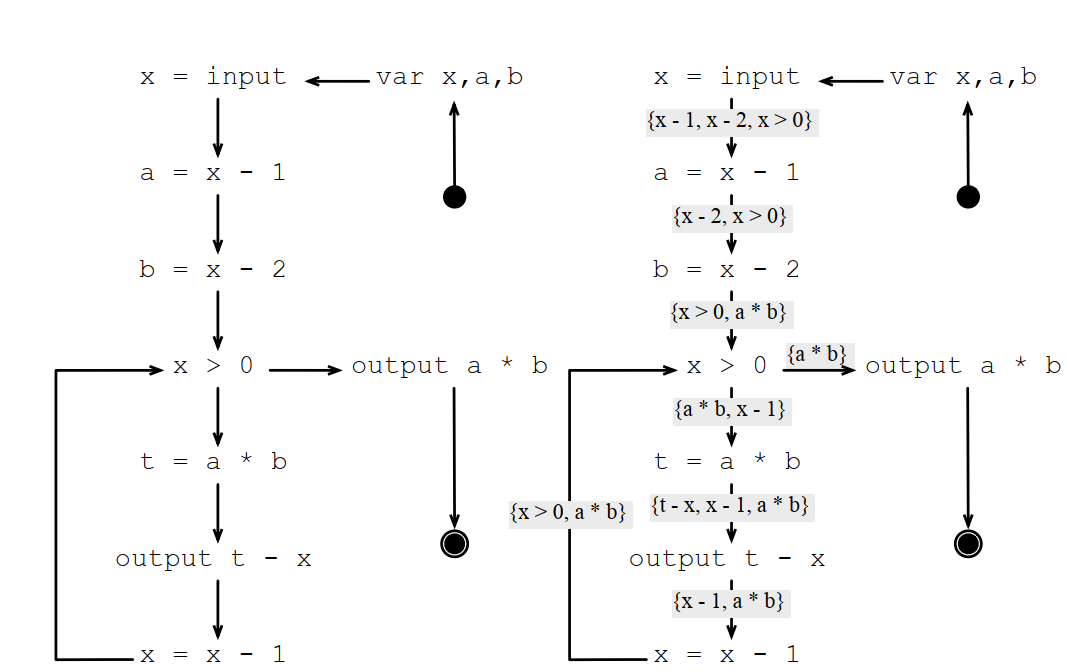
安全的代碼修改(Safe Code Hositing):如果某個修改,在任何場景下都不會導致程式做額外的工作,該修改就是安全的修改。
3.4 可獲得性定義(Reaching Definitions)
可獲得性定義:如果控制流圖上存在一條邊從程式點p到程式點p‘,並且這條邊上沒有任意一個結點對變數v重新定義,則稱為p在程式點p定義的變數v在程式的p'可獲得。
可獲得性的推導:變數v在程式點p可獲得當且僅當:
-
- 在p之前v可獲得,
- 並且v在p處沒有重新定義;
或者
-
- p處定義了變數v。
可獲得性定義的數據流等式:
對 p : v = E
IN(p) = ∪ OUT(ps), ps ∈ pred(p)
OUT(p) = ( IN(p) \ {defs(v)} )∪ {(p, v)}
IN(p) :p之前的可獲得性定義集合
OUT(p) :p之後的可獲得性定義集合
defs(v) :程式中所有v的定義集合
(p, v): p處定義的v
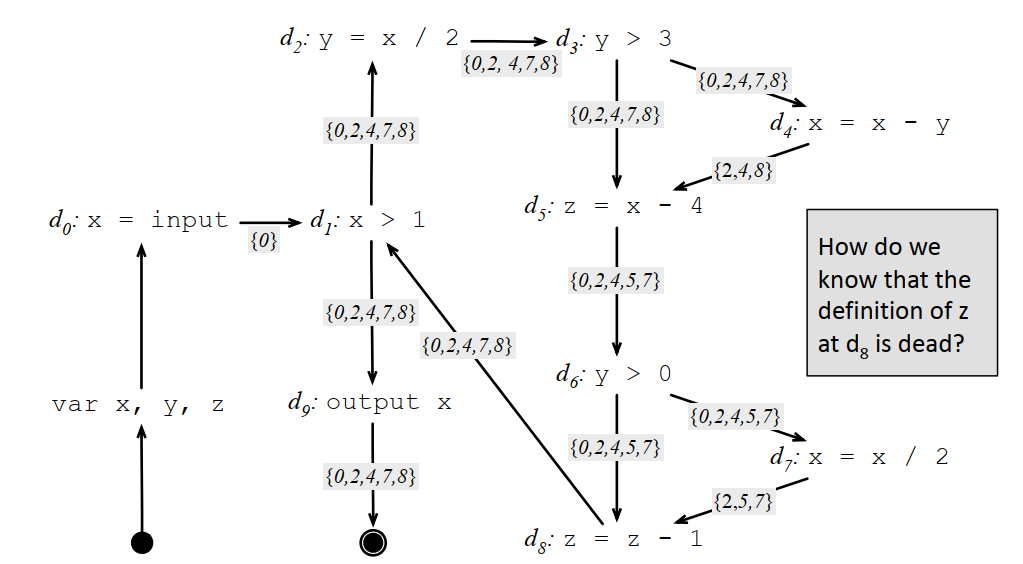
可獲得性定義的例子:
3.5 MONOTONE框架
3.5.1 幾種數據流分析方法的比較
本章學到了四種數據流分析方法:

數據流分析按彙總方向有正向分析和反向分析兩種。
正向分析是從程式的起始點往結束點方向分析,每次輸入都是通過這之前所有的輸出通過運算(交集或者並集)得到,輸出是基於p點的輸入和p點的表達式計算出來。例如本章講到的可獲得性定義和可訪問表達式的分析。
反向分析相反,需要從程式的結束點往起始點分析,分析方向和數據流動的方向相反。每次先計算輸出,每個p的輸出都是這之後的輸入通過運算得到,輸入是基於p點的輸出和p點的表達式計算出來。例如本章講到的生命周期分析和常用表達式分析。
按彙總方法有可以分為確定性分析(MUST,必須)和可能性分析(MAY,可以)2種。區別在於集合從多點匯聚到一個點的時候應該使用交集還是並集。
3.5.2 轉換函數
數據流分析過程需要對程式進行一些翻譯,數據流分析不能直接分析程式的具體語義(要不然就永遠分析不完了),而是分析一種抽象的語義。轉換函數就是抽取程式的抽象語義的函數。
正向分析的轉換函數是通過輸入生成輸出的函數:
OUT[s] = fs(IN[s])
相反,反向分析的轉換函數是通過輸出計算輸入的函數:
IN[s] = fs(OUT[s])
3.5.3 合併函數
合併函數確定多條岔路匯聚成一條路或者一條路分成多條岔路時的處理過程。

給定一個轉換函數,一個合併函數,和一個特定的初始化的IN和OUT的集合,能夠證明它必然導致抽象翻譯的正常結束。
數據流分析的過程就是按上面的框架找到一個轉換函數,和一個合併函數,並給定一個IN和OUT的初始集合。
3.5.4 數據流分析簡史
- Frances Allen got the Turing Award of 2007. Some of her contributions touch dataflow analyses.
- Allen, F. E., "Program Optimizations", Annual Review in Automatic Programming 5 (1969), pp. 239-307
- Allen, F. E., "Control Flow Analysis", ACM Sigplan Notices 5:7 (1970), pp. 1-19
- Kam, J. B. and J. D. Ullman, "Monotone Data Flow Analysis Frameworks", Actal Informatica 7:3 (1977), pp. 305-318
- Kildall, G. "A Unified Approach to Global Program Optimizations", ACM Symposium on Principles of Programming Languages (1973), pp. 194-206


