動態規劃

[P1216 USACO1.5][IOI1994]數字三角形 Number Triangles - 洛谷 | 電腦科學教育新生態 (luogu.com.cn)

題目描述

觀察下麵的數字金字塔。

寫一個程式來查找從最高點到底部任意處結束的路徑，使路徑經過數字的和最大。每一步可以走到左下方的點也可以到達右下方的點。

        7 
      3   8 
    8   1   0 
  2   7   4   4 
4   5   2   6   5 

在上面的樣例中，從 7→3→8→7→5 的路徑產生了最大

輸入格式

第一個行一個正整數 r ,表示行的數目。

後面每行為這個數字金字塔特定行包含的整數。

輸出格式

單獨的一行,包含那個可能得到的最大的和。

輸入輸出樣例

輸入 #1

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5 

輸出 #1

30

說明/提示

【數據範圍】
對於 100% 的數據，1≤ r ≤1000，所有輸入在 [0,100] 範圍內。

因為題目的樣例用貪心就能過,所以將樣例稍作改編

輸入 #2

5
7
3 8
8 1 0
2 4 4 7
4 5 2 6 5

輸出 #2

28

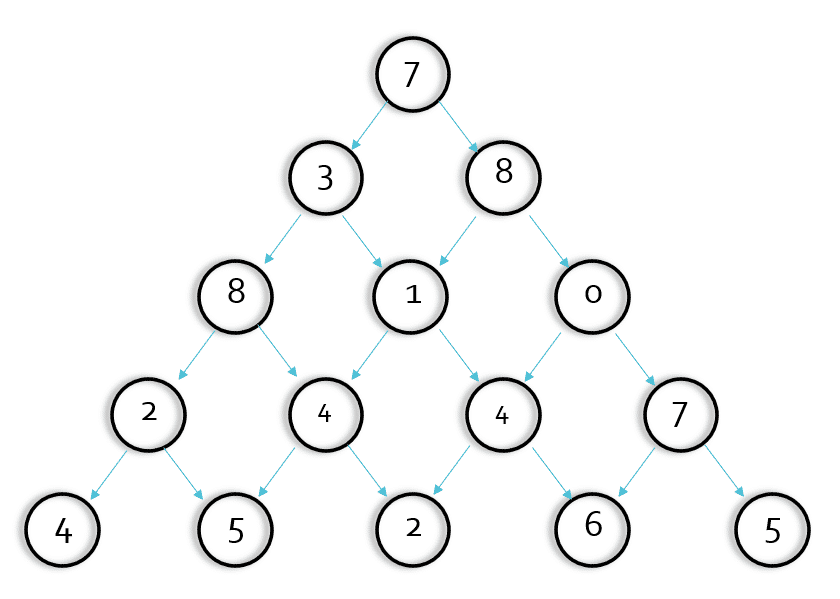
• 我們大部分人看到這道題腦海中都會浮現這樣的想法，是不是只要每步走的都是兩個點中較大的那個值，最後的答案就是最大的。就像這樣：7->8->1->4->6
• 我們會發現在第四步的時候情況不對，這裡兩個子節點相同,明顯取右側的4比左側的4結果要大，可是當程式執行到這一步，我們要如何使電腦明白要選擇右邊的結點而不是左邊的。

貪心策略

這種做法其實是一種貪心的思想,來看它的定義：

• 貪心演算法（又稱貪婪演算法）是指，在對問題求解時，總是做出在當前看來是最好的選擇。也就是說，不從整體最優上加以考慮，演算法得到的是在某種意義上的局部最優解。

我們會發現,即使在第四步選擇了右邊這個點,結果(7->8->1->4->6=26)比題目給出的答案7->8->0->7->6總和為28小.即題目在第三層就選擇了小的0而不是1。

正是因為我們每次選擇的時候只考慮當前的物品而沒有考慮後面的物品,而產生的決策錯誤.

因此我們可以知道貪心策略的限制條件，每次選擇局部最優解的時候，一定要保證局部最優策略不會對後續決策產生影響，如此才能使用貪心策略。

搜索演算法

我們再來考慮一種方法,既然貪心行不通,我們不妨考慮通過搜索來獲得它所有的結果.

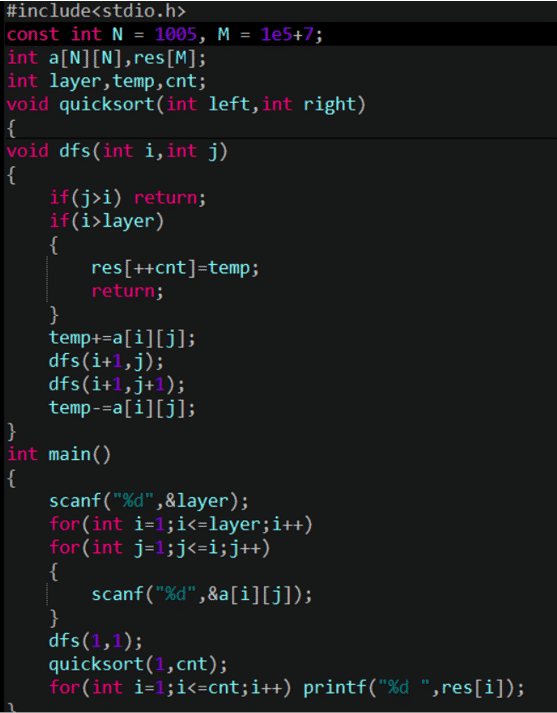
然而，會發現：在每一層每個結點都有兩種選擇,選擇左下或者右下，那麼數字三角形有 2^n-1條路線,我們既需要O(2^n-1)的時間,又需要2^n-1的空間，如果不進行剪枝當層數很大的時候這是行不通的。

我們考慮一下能不能把搜索優化。

首先,回到剛纔那個想法，在第 4 層 4 和 4 相同的情況下到底電腦應該選擇哪一個。此時，我們可以考慮讓電腦分別對這兩個結點進行搜索，搜索完再返回大的值，即我們要選擇的結點。

接著，我們想這種想法可不可以在兩個結點不相同的時候也使用。於是就有了我們從第一個結點開始，往下先對3和8進行搜索，3和8再分別對自己的子節點搜索…………搜索完後逐層向上返回最大值，這樣使得電腦在每次決策的時候選擇的都是最優的。

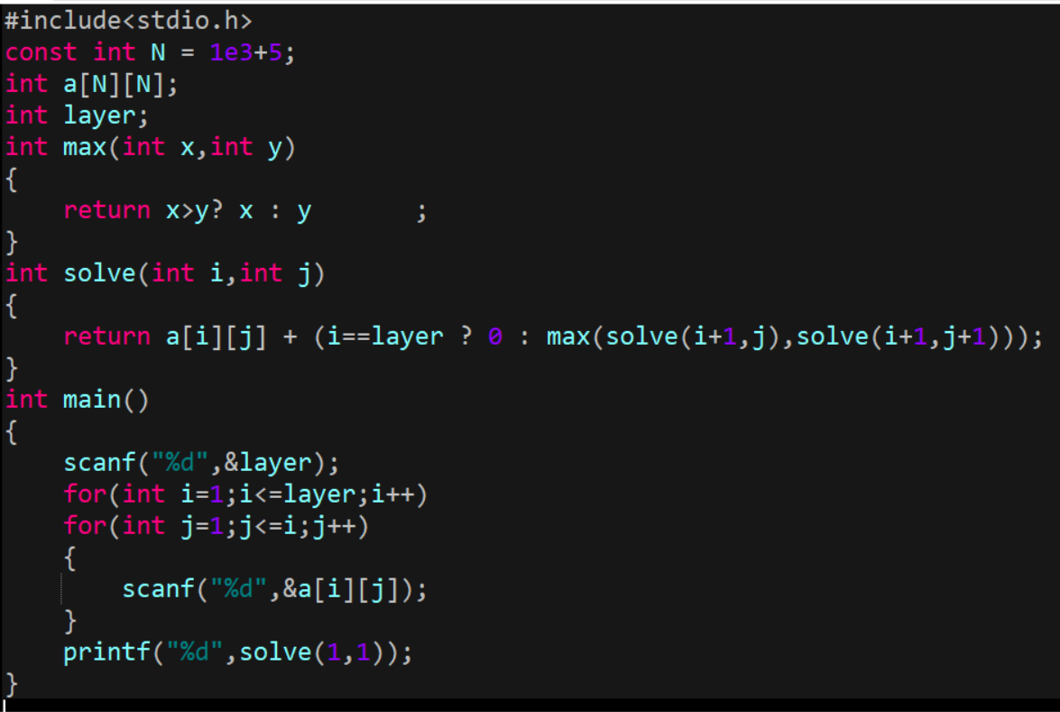
可惜,我們會發現,這個時間複雜度還是O(2^n-1)，因為還是每個結點要對底下的兩結點搜索。

NOT GIVE UP

我們反思一下剛纔的遞歸演算法

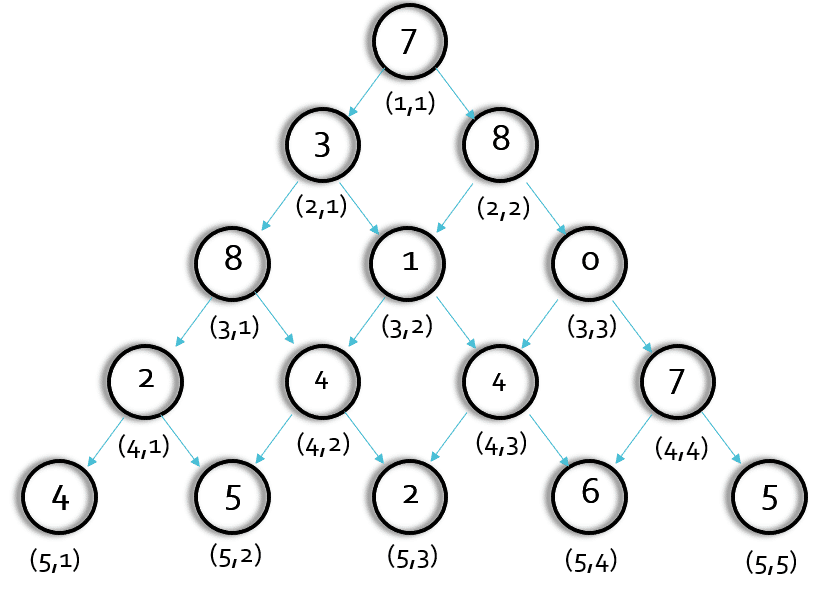
我們先把圖簡化，我們看第三層，是不是(2,1)和(2,2)均要執行一次solve(3,2)這個函數，即(3,2)這個點將要被執行兩次。

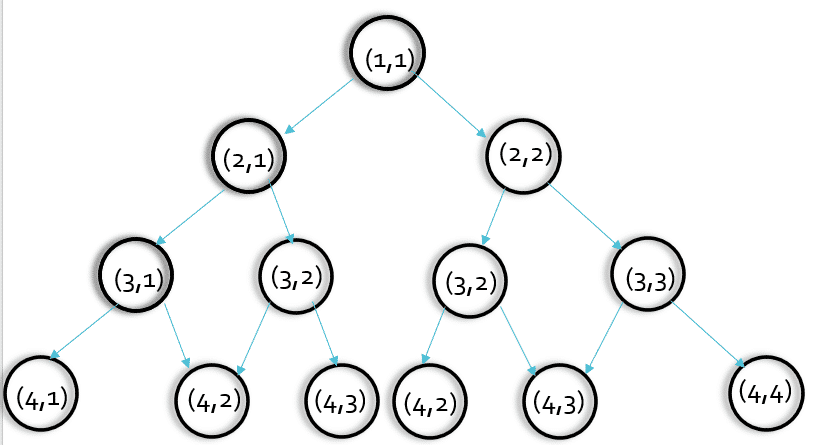
可能我們會認為，重覆算一兩個數影響不大，但是,我們以此類推，會發現(3,2)的子節點也會被搜索多次，這樣，當層數很多時重覆搜索的次數會很多，導致了時間的浪費(這就是-----重疊子問題)

我們想想，有什麼方法可以防止重覆搜索。

• a：當然是把它記下來！

我們考慮用一個二維數組 d[ i ][ j ] 來記錄這個遞歸的返回值。

int solve(int i,int j)
{
    d[i][j]=a[i][j]+(i==layer?0:max(solve(i+1,j),solve(i+1,j+1)));
    return d[i][j];
}

記錄好了，應該如何讓電腦明白“已經計算過了,不用再計算了”?

int solve(int i,int j)
{
    if(d[i][j]>=0) return d[i][j];
    d[i][j]=a[i][j]+(i==layer?0:max(solve(i+1,j),solve(i+1,j+1)));
    return d[i][j];
}

當 d[i][j] == 0 時表示已經計算過了，如果 d 數組初值為 0，每次搜索都會直接返回，所以我們還需要給d數組賦上初值，即在int main()函數中加入這樣一句。

memset(d,-1,sizeof d);

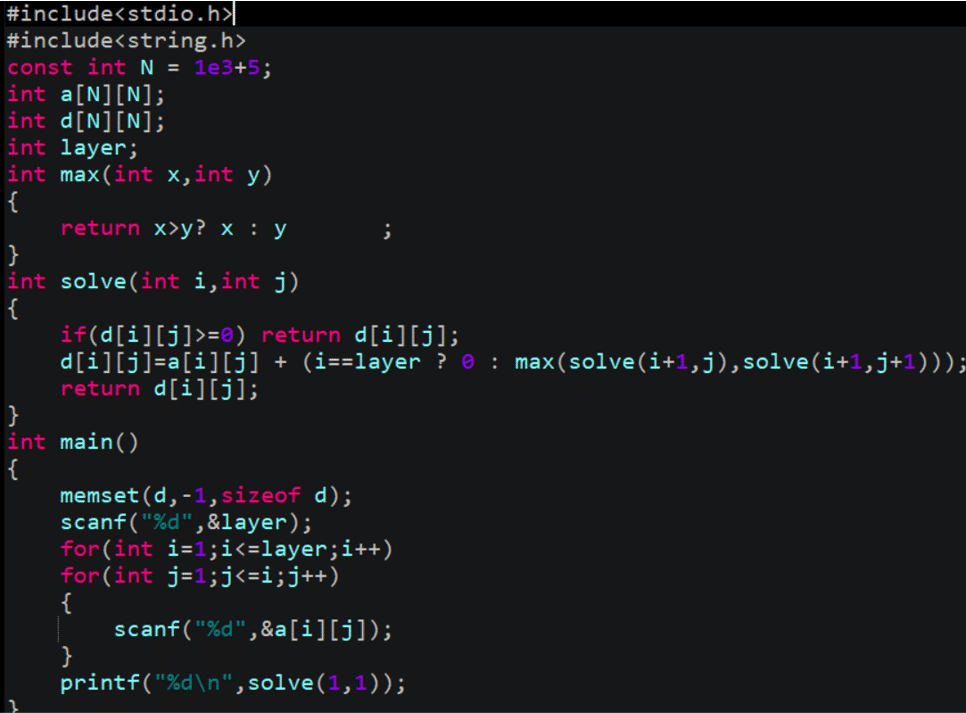
這就是記憶化搜索

由於我們儲存了每個結點遞歸的返回值，我們可以保證每個結點只被遞歸計算一次。所以時間複雜度是O(n²)，從2ⁿ~n²這是一個巨大的優化。

int solve(int i,int j)
{
    if(d[i][j]>=0) return d[i][j];
    d[i][j]=a[i][j]+(i==layer?0:max(solve(i+1,j),solve(i+1,j+1)));
    return d[i][j];
}

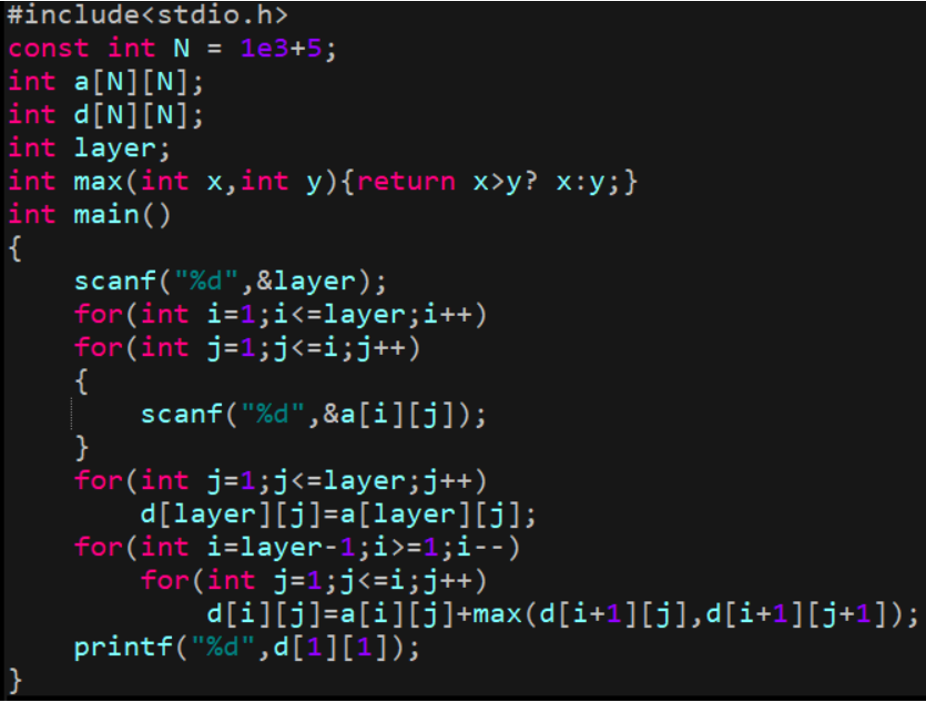
我們來考慮d(i,j)這個數組的意義，可以發現d(i,j)表示這個位置出發能得到的最大和(包括本身)。

我們把d(i,j)當成一個函數，那麼原問題就可以是求解d(1,1)這個值，即代入下麵這個數學函數。

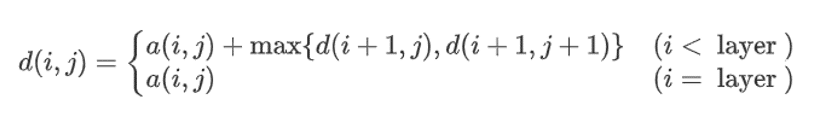
這樣,我們就引出了今天的主角-----動態規劃

什麼是動態規劃？

• 動態規劃(dynamic programming)是運籌學的一個分支，是求解決策過程(decision process)最優化的數學方法。20世紀50年代初美國數學家R.E.Bellman等人在研究多階段決策過程(multistep decision process)的優化問題時，提出了著名的最優化原理(principle of optimality)，把多階段過程轉化為一系列單階段問題，利用各階段之間的關係，逐個求解，創立瞭解決這類過程優化問題的新方法——動態規劃。1957年出版了他的名著《Dynamic Programming》，這是該領域的第一本著作。--------百度百科

簡單來說，dp是具有遞推形式的記憶化搜索，其核心思路是將大問題轉化為可以重覆被調用最優解的子問題並最終遞推出題目整體最優解。

在動態規劃的概念里，我們把d(i,j)定義為一個”狀態”，而這個方程就是所謂的”狀態轉移方程”。

而這個狀態體現的從 ( i , j ) 出發的最大總和，正是”最優子結構”，即”全局最優解包含局部最優解”，這就有效解決了貪心演算法中(局部最優解不一定是整體最優解)的問題。

在上面的記憶化搜索中，我們求解的方式是從方程左邊到方程右邊，而動態規劃正相反，從右邊推出左邊。

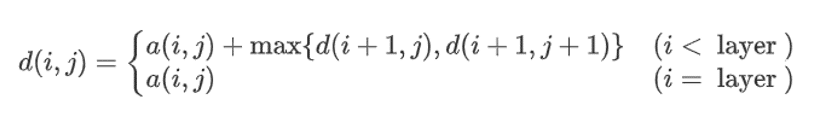
最後呈現的正是電腦決策的路徑。這一方法被我們稱為”遞推”。

總結

動態規劃的要素：1.初始狀態 2.遞推關係公式

動態規劃的特征：1.最優子結構 2.無後效性 3.重覆子問題

最優子結構：問題的最優解包含子問題的最優解

無後效性：某階段狀態只關心前面階段的狀態值。一旦確定，就不受之後階段的決策影響。

重覆子問題： 不同的決策序列，到達某個相同的階段時，可能會產生重覆的狀態。