經典排序演算法(C語言版)

来源:https://www.cnblogs.com/sprinining/archive/2022/05/06/16228485.html
-Advertisement-
Play Games

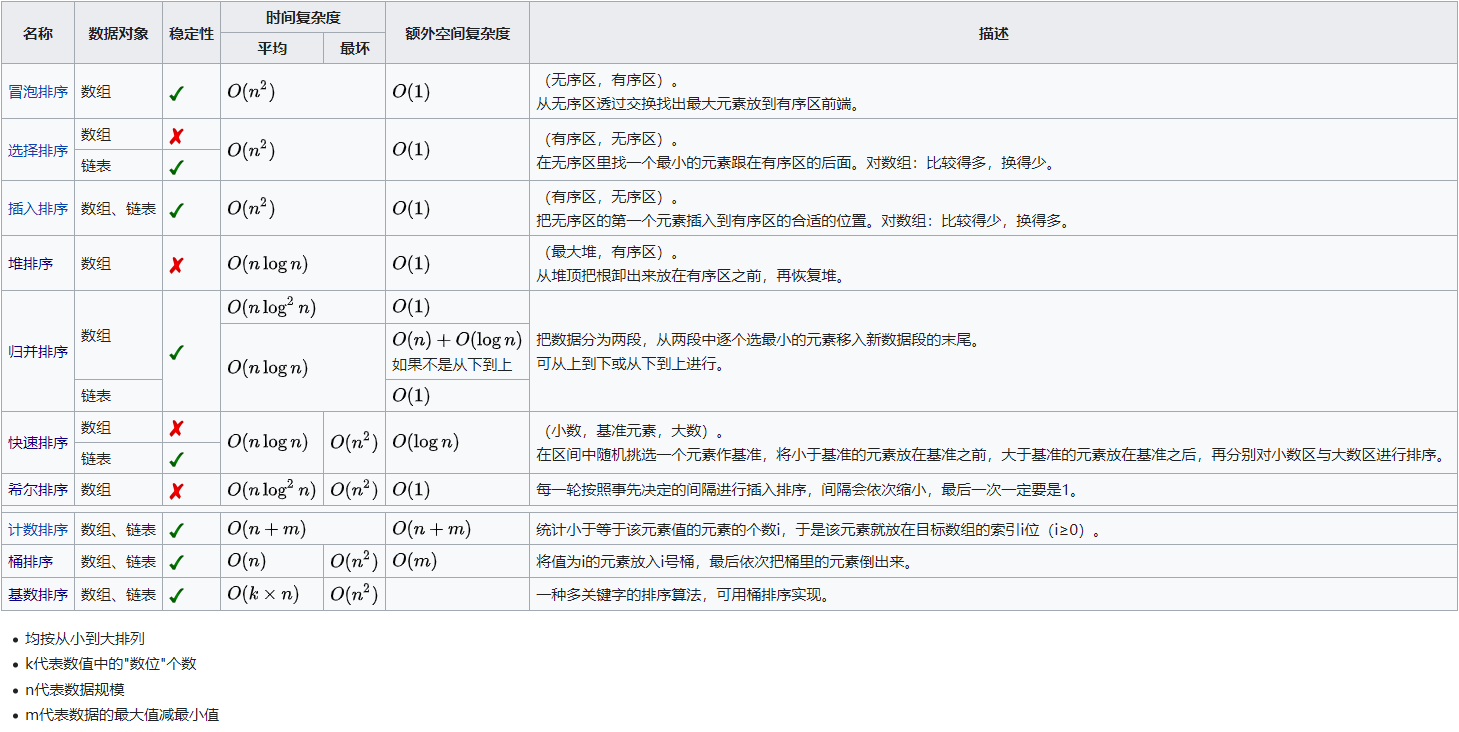
排序 比較 分類 比較排序的時間複雜度的下界O(nlogn) 對於n個待排序元素，在未比較時，可能的正確結果有n!種。在經過一次比較後，其中兩個元素的順序被確定，所以可能的正確結果剩餘n!/2種（確定之前兩個元素的前後位置的情況是相同，確定之後相當於少了一半的可能性）。依次類推，直到經過m次比較，剩 ...


排序

比較

分類

  • 比較排序的時間複雜度的下界O(nlogn)

    對於n個待排序元素，在未比較時，可能的正確結果有n!種。在經過一次比較後，其中兩個元素的順序被確定，所以可能的正確結果剩餘n!/2種（確定之前兩個元素的前後位置的情況是相同，確定之後相當於少了一半的可能性）。依次類推，直到經過m次比較，剩餘可能性n!/(2m)種。直到n!/(2m)<=1時，結果只剩餘一種。根據斯特靈公式，此時的比較次數m為o(nlogn)次。所以基於排序的比較演算法，最優情況下，複雜度是O(nlogn)的。

源碼

  • Sort.cpp
/**
 * @file Sort.cpp
 * @author Sprinining ([email protected])
 * @brief   交換排序：冒泡排序、快速排序
 *          選擇排序：普通選擇排序、堆排序
 *          插入排序：直接插入排序、二分插入排序、希爾排序
 *          歸併排序：普通歸併排序
 *          分佈排序：計數排序、桶排序、基數排序
 * @version 0.1
 * @date 2022-05-06
 *
 * @copyright Copyright (c) 2022
 *
 */

#include <math.h>
#include <stdio.h>
#include <stdlib.h>

int cmp(const void* a, const void* b) { return *(int*)(a) - *(int*)b; }

void swap(int* a, int* b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

// a, b不能是同一個地址的東西，否則會把該地址清零
void swap2(int* a, int* b) {
    *a = *a ^ *b;
    *b = *a ^ *b;
    *a = *a ^ *b;
}

void display(int* ary, int size) {
    for (int i = 0; i < size; i++) {
        printf("%d ", ary[i]);
    }
    puts("");
}

// 1.冒泡排序
void bubbleSort(int* array, int size) {
    // 比較size-1輪
    for (int i = 0; i < size - 1; i++) {
        // 是否已經有序了
        bool isSorted = true;
        // 每一輪都會有個大元素移到後面
        for (int j = 0; j < size - 1 - i; j++) {
            // 將相鄰的兩個比較，大的移到後面
            if (array[j] > array[j + 1]) {
                // 有交換的說明沒排好
                isSorted = false;
                swap(&array[j], &array[j + 1]);
            }
        }
        if (isSorted == true) break;
    }
    display(array, size);
}

void quickSortRecursive(int* array, int left, int right) {
    if (left >= right) return;
    int i = left;
    int j = right;
    // 基準元素
    int key = array[left];
    // 分成兩半，左邊小於基準元素，右邊大於基準元素
    while (i < j) {
        // 從右往左找第一個小於key的
        while (i < j && array[j] >= key) {
            j--;
        }
        // 與key交換
        if (i < j) {
            array[i] = array[j];
            // array[j]不用立刻放入key，後面可能會有比key大的元素防止這
            i++;
        }
        // 從左往右找第一個大於key的
        while (i < j && array[i] <= key) {
            i++;
        }
        // 與key交換
        if (i < j) {
            array[j] = array[i];
            j--;
        }
    }
    // 迴圈退出時i=j
    array[i] = key;
    quickSortRecursive(array, left, i - 1);
    quickSortRecursive(array, i + 1, right);
}

// 2.快速排序
void quickSort(int* array, int size) {
    quickSortRecursive(array, 0, size - 1);
    display(array, size);
}

// 3.普通選擇排序
void selectionSort(int* array, int size) {
    // size-1輪
    for (int i = 0; i < size - 1; i++) {
        int minIndex = i;
        // 從後面找更小的
        for (int j = i + 1; j < size; j++) {
            if (array[j] < array[minIndex]) {
                minIndex = j;
            }
        }
        // 確實有更小的
        if (minIndex != i) {
            swap(&array[i], &array[minIndex]);
        }
    }
    display(array, size);
}

// 自頂向下調整堆頂（只有堆頂不符合堆的定義）
void adjustHeap(int* array, int currentIndex, int size) {
    int temp = array[currentIndex];
    int leftChildIndex = 2 * currentIndex + 1;

    while (leftChildIndex <= (size - 1)) {
        // 找更大點的子節點
        if (leftChildIndex < (size - 1) &&
            array[leftChildIndex] < array[leftChildIndex + 1]) {
            leftChildIndex++;
        }
        if (array[leftChildIndex] <= temp) break;
        // 與子節點交換
        array[currentIndex] = array[leftChildIndex];
        currentIndex = leftChildIndex;
        leftChildIndex = 2 * currentIndex + 1;
    }
    array[currentIndex] = temp;
}

// 4.堆排序
void heapSort(int* array, int size) {
    // 從第一個非葉子節點開始，自底向上
    for (int i = (size - 2) / 2; i >= 0; i--) {
        adjustHeap(array, i, size);
    }
    printf("建堆：");
    display(array, size);
    // size-1輪
    for (int i = 1; i < size; i++) {
        swap(&array[0], &array[size - i]);
        // 已經是堆了，在修改完堆頂後只需要對堆頂進行重定位
        adjustHeap(array, 0, size - i);
    }
    display(array, size);
}

// 5.直接插入排序
void insertionSort(int* array, int size) {
    // size-1輪
    // [0, i-1]是有序序列
    for (int i = 1; i < size; i++) {
        // 待插入的元素
        int temp = array[i];
        // 插入已經有序的序列
        // 從有序序列的末尾往前找第一個小於等於temp的
        int j = i - 1;
        while (j >= 0 && (array[j] > temp)) {
            // 邊找邊把不符合的元素後移
            array[j + 1] = array[j];
            j--;
        }
        array[j + 1] = temp;
    }

    display(array, size);
}

// 6.二分插入排序
void binaryInsertionSort(int* array, int size) {
    for (int i = 1; i < size; i++) {
        int temp = array[i];
        // 二分查找插入位置
        int left = 0;
        int right = i - 1;
        int mid;
        while (left <= right) {
            mid = left + (right - left) / 2;
            if (array[mid] >= temp) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        // 迴圈結束後left就是應該插入的下標
        // 把下標從left到i-1的都往後移動一位
        for (int j = i - 1; j >= left; j--) {
            array[j + 1] = array[j];
        }
        array[left] = temp;
    }
    display(array, size);
}

// 7.希爾排序
void shellSort(int* array, int size) {
    // 步長（讓一個元素可以一次性地朝最終位置前進一大步）
    int gap = size / 2;
    while (gap > 0) {
        // 間隔gap的分在同一組(共gap組，gap下標[0,
        // gap-1]是這gap組每組的首個已排序元素)，進行普通的插入排序
        for (int i = gap; i < size; i++) {
            int temp = array[i];
            int j = i - gap;
            while (j >= 0 && array[j] > temp) {
                array[j + gap] = array[j];
                j -= gap;
            }
            array[j + gap] = temp;
        }
        printf("gap:%d\n", gap);
        display(array, size);
        gap = gap / 2;
    }
}

// 分治-治
void mergeSort_conquer(int* array, int left, int mid, int right, int* temp) {
    // [left, mid]和[mid+1, right]兩個有序數組
    int i = left;
    int j = mid + 1;
    int index = 0;
    while (i <= mid && j <= right) {
        if (array[i] < array[j]) {
            temp[index++] = array[i++];
        } else {
            temp[index++] = array[j++];
        }
    }
    // 剩餘元素直接放入temp
    while (i <= mid) {
        temp[index++] = array[i++];
    }
    while (j <= right) {
        temp[index++] = array[j++];
    }
    // 放回原數組
    index = 0;
    while (left <= right) {
        array[left++] = temp[index++];
    }
}

// 分治-分
void mergeSort_divide(int* array, int left, int right, int* temp) {
    if (left >= right) return;
    int mid = left + (right - left) / 2;
    // 左邊歸併排序
    mergeSort_divide(array, left, mid, temp);
    // 右邊歸併排序
    mergeSort_divide(array, mid + 1, right, temp);
    // 合併兩個有序序列
    mergeSort_conquer(array, left, mid, right, temp);
}

// 8.普通歸併排序
void mergeSort(int* array, int size) {
    int* temp = (int*)malloc(sizeof(int) * size);
    mergeSort_divide(array, 0, size - 1, temp);
    display(array, size);
}

// TODO: 迭代版歸併排序

// 9.計數排序(每個桶只存儲單一鍵值) 0~10
void countingSort(int* array, int size) {
    int* frequency = (int*)calloc(11, sizeof(int));
    // frequency[i]表示統計i出現的次數
    for (int i = 0; i < size; i++) {
        frequency[array[i]]++;
    }
    display(frequency, 11);
    // frequency[i]表示小於等於i的個數
    for (int i = 1; i < 11; i++) {
        frequency[i] += frequency[i - 1];
    }
    display(frequency, 11);

    int* sorted = (int*)calloc(size, sizeof(int));
    // 倒著遍歷原數組，把原數組放在新數組正確的位置上
    for (int i = size - 1; i >= 0; i--) {
        // 有frequency[array[i]]個小於等於array[i]個元素
        // 說明array[i]排在第frequency[array[i]]個位置，下標就是frequency[array[i]]-1
        // 放好後frequency[array[i]]要自減
        sorted[--frequency[array[i]]] = array[i];
        printf("frequency:\t");
        display(frequency, 11);
        printf("sorted:\t\t");
        display(sorted, size);
    }
}

typedef struct {
    int** bucket;
    int row;
    int column;
    int* index;
} Bucket;

// 10.桶排序(每個桶存儲一定範圍的數值)
// 數要相對均勻分佈，桶的個數也要合理設計(需要知道輸入數據的上界和下界和分佈情況)，桶排序是一種用空間換取時間的排序
void bucketSort(int* array, int size) {
    Bucket* b = (Bucket*)malloc(sizeof(Bucket));
    b->row = 5;
    b->column = 3;
    b->index = (int*)calloc(b->row, sizeof(int));
    b->bucket = (int**)malloc(sizeof(int) * b->row);
    for (int i = 0; i < b->row; i++) {
        b->bucket[i] = (int*)malloc(sizeof(int) * b->column);
    }
    // 放入桶
    for (int i = 0; i < size; i++) {
        int index = array[i] / 10;
        b->bucket[index][b->index[index]++] = array[i];
    }
    size = 0;
    // 對每個桶進行排序（可用其他演算法）
    for (int i = 0; i < b->row; i++) {
        qsort(b->bucket[i], b->column, sizeof(int), cmp);
        for (int j = 0; j < b->column; j++) {
            array[size++] = b->bucket[i][j];
        }
    }
    display(array, size);
}

// 11.基數排序(根據鍵值的每位數字來分配桶)
void radixSort(int* array, int size) {
    Bucket* b = (Bucket*)malloc(sizeof(Bucket));
    b->row = 10;
    b->column = 10;
    b->index = (int*)calloc(b->row, sizeof(int));
    // 臨時存放按某一位排好序的序列
    b->bucket = (int**)malloc(sizeof(int) * b->row);
    for (int i = 0; i < b->row; i++) {
        b->bucket[i] = (int*)malloc(sizeof(int) * b->column);
    }

    // 最大的數的位數為3
    for (int i = 0; i < 3; i++) {
        // 按某一位重新排序
        for (int j = 0; j < size; j++) {
            int index = (array[j] / (int)pow(10, i)) % 10;
            b->bucket[index][b->index[index]++] = array[j];
        }
        // 放回原數組
        int returnSize = 0;
        for (int j = 0; j < b->row; j++) {
            for (int k = 0; k < b->index[j]; k++) {
                array[returnSize++] = b->bucket[j][k];
            }
            // 重置下標數組
            b->index[j] = 0;
        }
    }

    display(array, size);
}

void testSort() {
    // int a[] = {1, 0, 7, 2, 10, 5, 2, 8, 6, 0};
    // display(a, 10);
    // bubbleSort(a, 10);
    // quickSort(a, 10);
    // selectionSort(a, 10);
    // heapSort(a, 10);
    // insertionSort(a, 10);
    // binaryInsertionSort(a, 10);
    // shellSort(a, 10);
    // mergeSort(a, 10);
    // countingSort(a, 10);

    // int b[] = {1, 8, 7, 44, 42, 46, 38, 34, 33, 17, 15, 16, 27, 28, 24};
    // display(b, 15);
    // bucketSort(b, 15);

    int c[] = {53, 3, 542, 748, 14, 77, 214, 154, 63, 616};
    radixSort(c, 10);
}

您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • ReentrantLock學習
    ReentrantLock ReentrantLock功能 ReentrantLock和synchronized一樣是可重入的 可重入即當線程擁有了鎖時，當該線程再次請求鎖資源的時候，線程是可以再次成功獲得的。 static ReentrantLock lock = new ReentrantLoc ...
  • PageObject（PO）設計模式在 UI 自動化中的實踐總結（以 QQ 郵箱登陸為例）
    Spring Ioc源碼分析系列--Ioc的基礎知識準備 本系列文章代碼基於Spring Framework 5.2.x Ioc的概念 在Spring里，Ioc的定義為The IoC Container，翻譯過來也就是Ioc容器。為什麼會被叫做容器呢？我們來比對一下日常生活中的容器，也就是那些瓶瓶罐 ...
  • Spring 源碼（8）Spring BeanPostProcessor的註冊、國際化及事件發佈機制
    上一篇文章https://www.cnblogs.com/redwinter/p/16198942.html介紹了Spring的註解的解析過程以及Spring Boot自動裝配的原理，大概回顧下：Spring 解析註解是通過BeanFactoryPostProcessor的子介面BeanDefini ...
  • 完了，我的小網站圖片掛了！
    大家好，我是二哥！ 很早之前，就有小伙伴給我反饋說《Java 程式員進階之路》經常有圖片不顯示或者載入緩慢。 但由於白嫖（GitHub圖床+jsdelivr CDN）的力量實在是太過強大了（狗頭），再加上我本人沒有遇到過這個問題，所以就一直拖延著，遲遲沒有行動。 直到某一天，我神秘的流量用光了，上不 ...
  • 【面試普通人VS高手系列】講一下wait和notify這個為什麼要在synchronized代碼塊中？
    一個工作七年的小伙伴，竟然不知道”wait”和“notify”為什麼要在Synchronized代碼塊裡面。 好吧，如果屏幕前的你也不知道，請在評論區打上”不知道“。 對於這個問題，我們來看看普通人和高手的回答。 普通人： 額。。。。。。。。。。。。 高手： wait和notify用來實現多線程之間 ...
  • Python 源代碼縮進格式化工具
    前言 昨天在跟小伙伴聊天，當他談起自己正在做的項目時，一臉愁容。 他吐槽道：“該項目的 Python 代碼庫由多個人共同維護。由於每個人使用的編輯器不同，每個人的編碼風格也不同，最終導致了 代碼的縮進千奇百怪：有縮進 2 個空格的，有縮進 4 個空格的，有縮進 8 個空格，有縮進一個 Tab 的，更 ...
  • Java 中 equals 的這些坑，千萬別踩。。。
    來源：cnblogs.com/juncaoit/p/12422752.html 一直以為這個方法是java8的，今天才知道是是1.7的時候，然後翻了一下源碼。 這篇文章中會總結一下與a.equals(b)的區別，然後對源碼做一個小分析。 值是null的情況 1、a.equals(b), a 是nul ...
  • 詳解 Java 17 中新推出的密封類
    Java 17推出的新特性Sealed Classes經歷了2個Preview版本（JDK 15中的JEP 360、JDK 16中的JEP 397），最終定稿於JDK 17中的JEP 409。Sealed Classes有兩種主流翻譯：密封類、封閉類。個人喜歡前者多一些，所以在本文中都稱為密封類。其 ...
一周排行
    -Advertisement-
    Play Games
  • UOS 開啟 VisualStudio 遠程調試 .NET 應用之旅
    前言 在我們開發過程中基本上不可或缺的用到一些敏感機密數據，比如SQL伺服器的連接串或者是OAuth2的Secret等，這些敏感數據在代碼中是不太安全的，我們不應該在源代碼中存儲密碼和其他的敏感數據，一種推薦的方式是通過Asp.Net Core的機密管理器。 機密管理器 在 ASP.NET Core ...
  • C# - 能否讓 SortedSet.RemoveWhere 內傳入的委托非同步執行
    新改進提供的Taurus Rpc 功能，可以簡化微服務間的調用，同時可以不用再手動輸出模塊名稱，或調用路徑，包括負載均衡，這一切，由框架實現並提供了。新的Taurus Rpc 功能，將使得服務間的調用，更加輕鬆、簡約、高效。 ...
  • 順序棧的介面程式
    順序棧的介面程式 目錄順序棧的介面程式頭文件創建順序棧入棧出棧利用棧將10進位轉16進位數驗證 頭文件 #include <stdio.h> #include <stdbool.h> #include <stdlib.h> 創建順序棧 // 指的是順序棧中的元素的數據類型，用戶可以根據需要進行修改 ...
  • mORMot2 獲取數據集1
    前言 整理這個官方翻譯的系列，原因是網上大部分的 tomcat 版本比較舊，此版本為 v11 最新的版本。 開源項目 從零手寫實現 tomcat minicat 別稱【嗅虎】心有猛虎，輕嗅薔薇。 系列文章 web server apache tomcat11-01-官方文檔入門介紹 web serv ...
  • 萬字長文總結與剖析C語言關鍵字 -- <<C語言深度解剖>>
    C總結與剖析:關鍵字篇 -- <<C語言深度解剖>> 目錄C總結與剖析:關鍵字篇 -- <<C語言深度解剖>>程式的本質:二進位文件變數1.變數:記憶體上的某個位置開闢的空間2.變數的初始化3.為什麼要有變數4.局部變數與全局變數5.變數的大小由類型決定6.任何一個變數,記憶體賦值都是從低地址開始往高地 ...
  • 【Flink入門修煉】2-3 Flink Checkpoint 原理機制
    如果讓你來做一個有狀態流式應用的故障恢復，你會如何來做呢？ 單機和多機會遇到什麼不同的問題？ Flink Checkpoint 是做什麼用的？原理是什麼？ ...
  • C++ 多級繼承與多重繼承：代碼組織與靈活性的平衡
    C++ 多級繼承 多級繼承是一種面向對象編程（OOP）特性，允許一個類從多個基類繼承屬性和方法。它使代碼更易於組織和維護，並促進代碼重用。 多級繼承的語法 在 C++ 中，使用 : 符號來指定繼承關係。多級繼承的語法如下： class DerivedClass : public BaseClass1 ...
  • 圖文結合手把手教你創建SpringCloud項目
    前言 什麼是SpringCloud？ Spring Cloud 是一系列框架的有序集合，它利用 Spring Boot 的開發便利性簡化了分散式系統的開發，比如服務註冊、服務發現、網關、路由、鏈路追蹤等。Spring Cloud 並不是重覆造輪子，而是將市面上開發得比較好的模塊集成進去，進行封裝，從 ...
  • 類模板的常見用法
    class_template 類模板和函數模板的定義和使用類似，我們已經進行了介紹。有時，有兩個或多個類，其功能是相同的，僅僅是數據類型不同。類模板用於實現類所需數據的類型參數化 template<class NameType, class AgeType> class Person { publi ...
  • system-v IPC共用記憶體通信
    目錄system v IPC簡介共用記憶體需要用到的函數介面shmget函數--獲取對象IDshmat函數--獲得映射空間shmctl函數--釋放資源共用記憶體實現思路註意 system v IPC簡介 消息隊列、共用記憶體和信號量統稱為system v IPC(進程間通信機制)，V是羅馬數字5，是UNI ...
所有分類