finally的特點 finally:被finally控制的語句體一定會執行 * 註意:如果在執行到finally之前jvm退出了,就不能執行了。 * * A:格式 * try...catch...finally... * B:用於釋放資源,在IO流操作和資料庫操作中會見到 package cn.i ...
背包問題的基本模型是:
有一個容量為C的背包,現在要從N件物品中選取若幹件裝入背包中,每件物品i的重量為W[i]、價值為P[i]。定義一種可行的背包裝載為:背包中物品的總重不能超過背包的容量,並且一件物品要麼全部選取、要麼不選取。定義最佳裝載是指所裝入的物品價值最高,並且是可行的背包裝載。
例如,設C= 12,N=4,W[4]={2,4,6,7},P[4]={ 6,10,12,13},則裝入W[1]和W[3],最大價值為23。
若採用貪心法來解決0/1背包問題,可能選擇的貪心策略一般有3種。每種貪心策略都是採用多步過程來完成背包的裝入,在每一步中,都是利用某種貪心準則來選擇將某一件物品裝入背包。
(1)選取價值最大者。
貪心策略為:每次從剩餘的物品中,選擇可以裝入背包的價值最大的物品裝入背包。這種策略不能保證得到最優解。例如,設C=30,有3個物品A、B、C,W[3]={28,12,12},P[3]={30,20,20}。根據策略,首先選取物品A,接下來就無法再選取了,此時最大價值為30。但是,選取裝B和C,最大價值為40,顯然更好。
(2)選取重量最小者。
貪心策略為:從剩下的物品中,選擇可以裝入背包的重量最小的物品裝入背包。其想法是通過多裝物品來獲得最大價值。這種策略同樣不能保證得到最優解。例如,設C=30,有3個物品A、B、C,W[3]={13,14,15},P[3]={20,30,40}。根據策略,首先選取物品A,接下來選取B,之後就無法再選取了,此時最大價值為50。但是,選取裝B和C,最大價值為70,顯然更好。
(3)選取單位重量價值最大者
貪心策略為:從剩餘物品中,選擇可裝入背包的P[i]/W[i]值最大的物品裝入。這種策略還是不能保證得到最優解。例如,設C=40,有3個物品A、B、C,W[3]={15,20,28},P[3]={15,20,30}。按照策略,首先選取物品C(p[2]/w[2]>1),接下來就無法再選取了,此時最大價值為30。但是,選取裝A和B,最大價值為35,顯然更好。
由上面的分析可知,採用貪心法並不一定可以求得最優解。
背包問題用貪心和搜索求解的效果不佳,其標準的解法是動態規劃。
1.編程思路1。
按每一件物品裝包為一個階段,共分為n個階段。

(1)建立遞推關係
設f[i][j]為背包容量j,可取物品範圍為i、i+1、…、n的最大效益值。例如,f[1][c]的含義是容量為c的背包、可在1~n件物品中選擇物品裝入背包後所得的最大效益值。
當0≤j<w[i] 時,物品i不可能裝入。最大效益值與f[i+1][j] 相同。
當j≥w[i] 時,有兩個選擇:
1)不裝入物品i,這時最大效益值為f[i+1][j] ;
2)裝入物品i,這時已產生效益p[i],背包剩餘容量 j−w[i],可以選擇物品i+1、…、n來裝,最大效益值為f[i+1][j−w[i]] + p[i]。
期望的最大效益值是兩者中的最大者。於是遞推關係(或稱狀態轉移方程)如下:
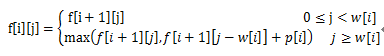
其中w[i]、p[i] 均為正整數,i=1、2、…、n。
邊界條件為: f[n][j]=p[n] 當j≥w[n] 時 (最後1件物品可裝包) ;
f[n][j]=0 當 j<w[n] 時 (最後1件物品不能裝包)。
所求最大效益即最優值為f[1][c]。
(2)逆推計算最優值
for (j=0;j<=c;j++) // 首先計算邊界條件f[n][j]
if (j>=w[n])
f[n][j]=p[n];
else
f[n][j]=0;
for(i=n-1;i>=1;i--) // 逆推計算f[i][j] (i從n-1到1)
for(j=0;j<=c;j++)
if (j>=w[i] && f[i+1][j]<f[i+1][j-w[i]]+p[i])
f[i][j]= f[i+1][j-w[i]]+p[i];
else
f[i][j]=f[i+1][j];
printf("最優值為%d\n",f[1][c]);
(3)構造最優解
若f[i][cw] > f[i+1][cw] ( i=1、2、…、n−1, cw的初始值為c)
則x[i]=1; 裝載w[i], cw=cw−x[i]*w[i]。
否則,x[i]=0,不裝載w[i]。
最後,所裝載的物品效益之和與最優值比較,決定w[n]是否裝載。
2.源程式1及運行結果。
#include <stdio.h> #define MAXN 500 #define MAXC 50000 int f[MAXN][MAXC]; int main() { int p[MAXN],w[MAXN]; int n,c; printf("請輸入物品的個數 N:"); scanf("%d",&n); printf("請輸入背包容量 C:"); scanf("%d",&c); printf("請依次輸入每種物品的重量:"); int i,j; for (i=1;i<=n;i++) scanf("%d",&w[i]); printf("請依次輸入每種物品的價值:"); for (i=1;i<=n;i++) scanf("%d",&p[i]); for (j=0;j<=c;j++) // 首先計算邊界條件f[n][j] if (j>=w[n]) f[n][j]=p[n]; else f[n][j]=0; for (i=n-1;i>=1;i--) // 逆推計算f[i][j] (i從n-1到1) for(j=0;j<=c;j++) if (j>=w[i] && f[i+1][j]<f[i+1][j-w[i]]+p[i]) f[i][j]= f[i+1][j-w[i]]+p[i]; else f[i][j]=f[i+1][j]; int cw=c; printf("背包所裝物品如下:\n"); printf(" i w(i) p(i) \n"); printf("----------------------\n"); int sp=0,sw=0; for (i=1;i<=n-1;i++) // 以表格形式輸出結果 if (f[i][cw]>f[i+1][cw]) { cw-=w[i]; sw+=w[i]; sp+=p[i]; printf("%3d %8d %8d\n",i,w[i],p[i]); } if (f[1][c]-sp==p[n]) { sw+=w[n];sp+=p[n]; printf("%3d %8d %8d\n",n,w[n],p[n]); } printf("裝載物品重量為 %d ,最大總價值為 %d\n",sw,sp); return 0; }
編譯並執行以上程式,可得到如下所示的結果。
請輸入 n 值:6
請輸入背包容量:60
請依次輸入每種物品的重量:15 17 20 12 9 14
請依次輸入每種物品的價值:32 37 46 26 21 30
背包所裝物品如下:
i w(i) p(i)
----------------------
2 17 37
3 20 46
5 9 21
6 14 30
裝載物品重量為 60 , 最大總價值為 134
3.編程思路2。
思路1中採用逆推的方法來求解的。實際上在應用動態規劃時,還可以順推求解。
(1)建立遞推關係
設f[i][j]為背包容量j,可取物品範圍為1、2、…、i的最大效益值。
當0≤j<w[i] 時,物品i不可能裝入。最大效益值與f[i−1][j] 相同。
當j≥w[i] 時,有兩種選擇:
1)不裝入物品i,這時最大效益值為f[i−1][j] ;
2)裝入物品i,這時已產生效益p[i],背包剩餘容量j−w[i],可以選擇物品1、2、…、i−1來裝,最大效益值為f[i−1][j−w[i]]+p[i] 。
期望的最大效益值是兩者中的最大者。於是有遞推關係
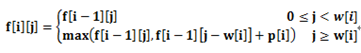
邊界條件為: f[1][ j]= p[1] 當 j≥w[1] 時;
f[1][ j] = 0 當j<w[1] 時。
所求最大效益即最優值為f[n][c]。
(2)順推計算最優值
for(j=0;j<=c;j++) // 首先計算邊界條件f[1][j]
if (j>=w[1] ) f[1][j]=p[1];
else f[1][j]=0;
for (i=2;i<=n;i++) // 順推計算f[i][j] (i從2到n)
for (j=0;j<=c;j++)
if(j>=w[i] && f[i-1][j]<f[i-1][j-w[i]]+p[i])
f[i][j]= f[i-1][j-w[i]]+p[i];
else f[i][j]=f[i-1][j];
printf("最優值為%d\n",f[n][c]);
(3)構造最優解
若f[i][cw] > f[i-1][cw] ( i=1、2、…、n−1, cw的初始值為c)
則x[i]=1; 裝載w[i], cw=cw−x[i]*w[i]。
否則,x[i]=0,不裝載w[i]。
最後,所裝載的物品效益之和與最優值比較,決定w[1]是否裝載。
4.源程式2及運行結果。
#include <stdio.h> #define MAXN 500 #define MAXC 50000 int f[MAXN][MAXC]; int main() { int p[MAXN],w[MAXN]; int n,c; printf("請輸入物品的個數 N:"); scanf("%d",&n); printf("請輸入背包容量 C:"); scanf("%d",&c); printf("請依次輸入每種物品的重量:"); int i,j; for (i=1;i<=n;i++) scanf("%d",&w[i]); printf("請依次輸入每種物品的價值:"); for (i=1;i<=n;i++) scanf("%d",&p[i]); for(j=0;j<=c;j++) // 首先計算邊界條件f[1][j] if(j>=w[1] ) f[1][j]=p[1]; else f[1][j]=0; for(i=2;i<=n;i++) // 順推計算f[i][j] (i從2到n) for(j=0;j<=c;j++) if(j>=w[i] && f[i-1][j]<f[i-1][j-w[i]]+p[i]) f[i][j]= f[i-1][j-w[i]]+p[i]; else f[i][j]=f[i-1][j]; int cw=c; printf("背包所裝物品如下:\n"); printf(" i w(i) p(i) \n"); printf("----------------------\n"); int sp=0,sw=0; for (i=n;i>=2;i--) // 以表格形式輸出結果 if(f[i][cw]>f[i-1][cw]) { cw-=w[i]; sw+=w[i]; sp+=p[i]; printf("%3d %8d %8d\n",i,w[i],p[i]); } if(f[n][c]-sp==p[1]) { sw+=w[1];sp+=p[1]; printf("%3d %8d %8d\n",1,w[1],p[1]); } printf("裝載物品重量為 %d ,最大總價值為 %d\n",sw,sp); return 0; }
編譯並執行以上程式,得到如下所示的結果。
請輸入 n 值:6
請輸入背包容量:60
請依次輸入每種物品的重量:15 17 20 12 9 14
請依次輸入每種物品的價值:32 37 46 26 21 30
背包所裝物品如下:
i w(i) p(i)
----------------------
6 14 30
5 9 21
3 20 46
2 17 37
裝載物品重量為 60 , 最大總價值為 134
5.編程思路3。
仔細分析編程思路2及其源程式可發現,第 i 件物品的選取決策只與第i-1件有關,與其他無關,即f[i][j]只與f[i-1][j]有關,f[i-2][*]、f[i-3][*]、…這些存儲空間的數據是不會再使用的,空間就浪費了。如果採用一維數組,新的狀態直接覆蓋在舊的上面,迭代使用,就可把空間複雜度從O(N*C)優化為O(C)。
(1)建立遞推關係
設f[j]為背包裝載的物品容量不超過j時,可獲得的最大效益值。
當0≤j<w[i] 時,物品i不可能裝入。f[j]的值不改變,無需處理。
當j≥w[i] 時,有兩種選擇:
1)不裝入物品i,這時最大效益值為f[j] ;
2)裝入物品i,這時會產生效益p[i],這實際上是在背包容量為j−w[i]的背包中裝入物品i,最大效益值為f[j−w[i]]+p[i] 。
期望的最大效益值是兩者中的最大者。於是有遞推關係
f[j]=max(f[j],f[j-w[i]]+p[i])
所求最大效益即最優值為f[c]。
(2)逆推計算最優值。
在前面使用二維數組時,為了計算最優值,採用順推和逆推的方法都可以,因為使用二維數組時,中間的所有狀態都保留了下來。
但是,使用一維數組時,究竟是使用順推還是逆推,就需要看具體的問題了。
由於本題中每個物品要麼不裝入,要麼只能裝入1次(每個物品只有1件)。因此,只能採用逆推的方法計算最優值。寫成如下的迴圈。
for (i=1;i<=n;i++) // 對每個物品進行處理
for(j=c;j>=w[i];j--) // 逆推計算f[j]
f[j]=max(f[j], f[j-w[i]]+p[i]);
為什麼要逆序枚舉計算呢?
如果是正序枚舉的話,迴圈寫成
for (i=1;i<=n;i++) // 對每個物品進行處理
for(j=w[i];j<=c;j++) // 正序(順序)計算f[j]
f[j]=max(f[j], f[j-w[i]]+p[i]);
下麵我們用簡單的測試數據作為示例進行詳細說明。
設背包容量C=8,有兩件物品,重量分別為w1=2,w2=3;價值分別為p1=3,p2=4。
初始時,f[0]~f[8]全部為0,背包沒有裝入任何物品,其裝入價值顯然為0。
採用正序枚舉時,當i=1,處理第1件物品,依次的計算過程如下:
f[2]=max { f[2], f[2-w1]+p1 } =max { 0, 0+3} =3
f[3]=max { f[3], f[3-w1]+p1 } =max { 0, 0+3} =3
f[4]=max { f[4], f[4-w1]+p1 } =max { 0, f[2]+3} = 6 (這裡實際就出問題了,因為第1件物品只有1件,在計算f[2]時裝入了1次,這裡又裝入1次,不可能的)
f[5]=max { f[5], f[5-w1]+p1 } =max { 0, f[3]+3} =6 (同上,第1件物品又裝入了1次)
f[6]=max { f[6], f[6-w1]+p1 } =max { 0, f[4]+3} =9 (第1件物品裝入了3次)
f[7]=max { f[7], f[7-w1]+p1 } =max { 0, f[5]+3} =9 (同上,第1件物品裝入了3次)
f[8]=max { f[8], f[8-w1]+p1 } =max { 0, f[6]+3} =12 (第1件物品裝入了4次)
當i=2,處理第2件物品,依次的計算過程如下:
f[3]=max { f[3], f[3-w2]+p2 } =max { 3, f[0]+4} =4 (第2件物品裝入了1次)
f[4]=max { f[4], f[4-w2]+p2 } =max { 6, f[1]+4} =6 (實際是第1件物品裝入2次)
f[5]=max { f[5], f[5-w2]+p2 } =max { 6, f[2]+4} =7 (第1件物品裝入1次,第2件物品裝入1次)
f[6]=max { f[6], f[6-w2]+p2 } =max { 9, f[3]+4} =9 (實際是第1件物品裝入3次)
f[7]=max { f[7], f[7-w2]+p2 } =max { 9, f[4]+4} =10 (實際是第1件物品裝入2次,第2件物品裝入1次)
f[8]=max { f[8], f[8-w2]+p2 } =max { 12, f[5]+4} =12 (實際是第1件物品裝入4次)
迴圈處理結束後,最優值f[8]=12,這顯然是不對的,因為只有2件物品,全部裝入背包,最大價值也只有3+4=7。
如果採用逆序枚舉,我們再來分析迴圈的處理過程。
當i=1,處理第1件物品,依次的計算過程如下:
f[8]=max { f[8], f[8-w1]+p1 } =max { 0, f[6]+3} =3 (物品1裝入背包,背包容量為8)
f[7]=max { f[7], f[7-w1]+p1 } =max { 0, f[5]+3} =3 (物品1裝入背包,背包容量為7)
f[6]=max { f[6], f[6-w1]+p1 } =max { 0, f[4]+3} =3 (物品1裝入背包,背包容量為6)
f[5]=max { f[5], f[5-w1]+p1 } =max { 0, f[3]+3} =3 (物品1裝入背包,背包容量為5)
f[4]=max { f[4], f[4-w1]+p1 } =max { 0, f[2]+3} =3 (物品1裝入背包,背包容量為4)
f[3]=max { f[3], f[3-w1]+p1 } =max { 0, f[1]+3} =3 (物品1裝入背包,背包容量為3)
f[2]=max { f[2], f[2-w1]+p1 } =max { 0, f[0]+3} =3 (物品1裝入背包,背包容量為2)
也就是,物品1的重量為2,可裝入背包容量為2~8的背包中,得到最大價值為3。
當i=2,處理第2件物品,依次的計算過程如下:
f[8]=max { f[8], f[8-w2]+p2 } =max { 3, f[5]+4} =7 (實際是物品1和物品2裝入背包)
f[7]=max { f[7], f[7-w2]+p2 } =max { 3, f[4]+4} =7 (實際是物品1和物品2裝入背包)
f[6]=max { f[6], f[6-w2]+p2 } =max { 3, f[3]+4} =7 (實際是物品1和物品2裝入背包)
f[5]=max { f[5], f[5-w2]+p2 } =max { 3, f[2]+4} =7 (實際是物品1和物品2裝入背包)
f[4]=max { f[4], f[4-w2]+p2 } =max { 3, f[1]+4} =4 (實際是物品2裝入背包)
f[3]=max { f[3], f[3-w2]+p2 } =max { 3, f[0]+4} =4 (實際是物品2裝入背包)
由上面的計算過程知,逆推計算時,每個物品若裝入背包,最多裝入1次。
由上面的分析大家也可產生一個印象,若每種物品只有1件,1個物品裝入背包最多只能裝入1次,則採用逆序遞推的方法計算最優值,這也是0/1背包的基本模式;若每種物品有無數件,可以不限次數地裝入背包中,則採用順序(正序)遞推的方法計算最優值,這也是完全背包的基本模式。對於0/1背包和完全背包,後面會進行更詳細地闡述。
(3)構造最優解。
如果要求輸出某個最優解,需要記錄每個狀態的最優值是由狀態轉移方程的哪一項推出來的。
如果我們知道了當前狀態是由哪一個狀態推出來的,就能容易的輸出某個最優解了。
為此,最簡單的方法是定義數組g[n][C],其中g[i][j]就記錄第i件物品在加入背包時,其狀態f[j]是由狀態轉移方程f[j]=max(f[j], f[j-w[i]]+p[i])哪一項推出。若第i件物品加入了背包,即f[j]= f[j-w[i]]+p[i],置g[i][j]=1;若第i件物品不加入背包,即f[j]=f[j],置g[i][j]=0。
改寫上面的逆推計算最優值迴圈如下。
for (i=1;i<=n;i++) // 對每個物品進行處理
for(j=c;j>=w[i];j--) // 逆推計算f[j]
{
if (f[j]<f[j-w[i]]+p[i])
{
f[j]=f[j-w[i]]+p[i];
g[i][j]=1; // 選擇第i件物品裝入
}
else
g[i][j]=0; // 不選擇第i件物品裝入
}
由此,可用如下迴圈輸出某個最優解。
int T=c;
for (i=n;i>=1;i--)
{
if (g[i][T])
{
printf("used %d",i);
T-=w[i]; //減去物品i的重量
}
}
當然,為了輸出某個最優解,我們又定義了一個二維數組,這樣我們採用一維數組進行優化的目的並沒有達到,還不如直接像編程思路1或編程思路2那樣,直接採用二維數組保存各狀態,再構造出最優解。
但是,如果只要求得到最優值,而無需輸出某個最優解,採用一維數組解決問題還是非常有意義的。
6.源程式3及運行結果。
#include <stdio.h> #define MAXN 500 #define MAXC 50000 int f[MAXC]={0}; int g[MAXN][MAXC]; int main() { int n,c; printf("請輸入物品的個數 N:"); scanf("%d",&n); printf("請輸入背包容量 C:"); scanf("%d",&c); printf("請依次輸入每種物品的重量:"); int p[MAXN],w[MAXN]; int i,j; for (i=1;i<=n;i++) scanf("%d",&w[i]); printf("請依次輸入每種物品的價值:"); for (i=1;i<=n;i++) scanf("%d",&p[i]); for (i=1;i<=n;i++) // 對每個物品進行處理 for(j=c;j>=w[i];j--) // 逆推計算f[j] { if (f[j]<f[j-w[i]]+p[i]) { f[j]=f[j-w[i]]+p[i]; g[i][j]=1; // 選擇第i件物品裝入 } else g[i][j]=0; // 不選擇第i件物品裝入 } printf("背包所裝物品如下:\n"); printf(" i w(i) p(i) \n"); printf("----------------------\n"); int t=c; for (i=n;i>=1;i--) { if (g[i][t]) { printf("%3d %8d %8d\n",i,w[i],p[i]); t-=w[i]; // 減去物品i的重量 } } printf("裝載物品重量為 %d ,最大總價值為 %d\n",c-t,f[c]); return 0; }
編譯並執行以上程式,得到如下所示的結果。
請輸入物品的個數 N:6
請輸入背包容量 C:60
請依次輸入每種物品的重量:15 17 20 12 9 14
請依次輸入每種物品的價值:32 37 46 26 21 30
背包所裝物品如下:
i w(i) p(i)
----------------------
6 14 30
5 9 21
3 20 46
2 17 37
裝載物品重量為 60 ,最大總價值為 134



