演算法效率的度量方法; 函數調用的時間複雜度分析; 常見的時間複雜度; 演算法的空間複雜度; ...
演算法效率的度量方法:
1. 事後統計方法:通過設計好的測試程式和數據,利用電腦計時器對不同演算法編製的程式的運行時間進行比較,從而確定演算法效率的高低。
缺陷:是根據以及編製好的程式去測試,如果測試的是糟糕的演算法,會功虧一簣。
2. 事前分析估算方法:在電腦程式編寫前,依據統計方法對演算法進行估算。
高級語言編寫的程式在電腦上運行時所消耗的時間取決於下列因素:
- 演算法採用的策略,方案。
- 編譯產生的代碼質量
- 問題的輸入規模
- 機器執行指令的速度
所以:一個程式的運行時間依賴於演算法的好壞和問題的輸入規模。
在編寫程式的時候,我們不關心語言、所用的電腦只關心它所實現的演算法。
在分析程式的運行時間的時候,最重要的是把程式看成是獨立於程式設計語言的演算法或一系列步驟,把基本操作的數量和輸入模式進行關聯。
函數漸進增長:

n=1時,演算法A1效率不如演算法B1;當n=2時,兩者效率相等;當n>2時,演算法A1開始優於演算法B1,隨著n的繼續增加,演算法A1比演算法B1逐漸拉大差距。所以總體上演算法A1比演算法B1優秀
定義:給定2個函數f(n)和g(n),如果存在一個整數N,使得對於所有的n>N,f(n)總是比g(n)大,那麼,我們說f(n)的增長漸進快於g(n)
例如如下演算法的增長率:
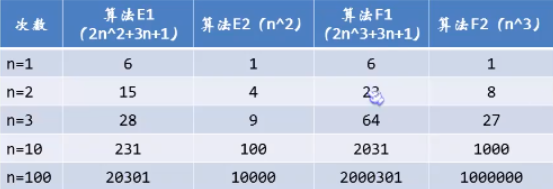
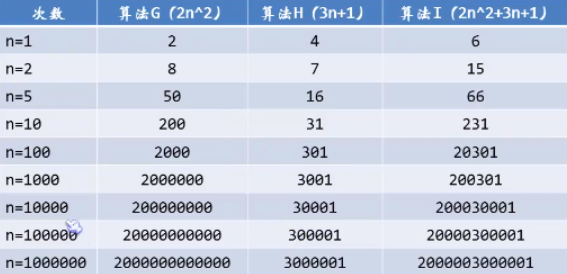
通過這組數據可以看出,當n的值非常大的時候,3n+1已經不能和2n^2的結果進行比較,最終幾乎是可以忽略不計的,演算法G在跟演算法I基本已經重合了,
結論:判斷一個演算法的時候,函數中的常數和其他次要項常常可以忽略,關註主項(最高項)的階數。
註意:不能通過少量的數據來判斷一個演算法的好壞。
演算法時間複雜度:
定義:在進行演算法分析時,語句總的執行次數T(n)是關於問題規模n的函數,進而分析T(n)隨n的變化情況並確定T(n)的數量級,演算法的時間複雜度,也就是演算法的時間量度,記作:T(n)=O(f(n))。他表示隨問題規模n的增大,演算法執行時間的增長率和f(n)的增長率相同,稱作演算法的漸進時間複雜度,簡稱為時間複雜度,其中f(n)是問題規模n的某個函數。
用大O()來體現演算法時間複雜度的記法,一般情況下隨著輸入規模n的增大,T(n)增長最慢的演算法為最優演算法。
推導大O階的方法
- 用常數1取代運行時間中的所有加法常數。
- 在修改後的運行函數中,只保留最高項。
- 如果最高項存在且不是1,則除這個項相乘的常數。
- 得到的最後的結果就是O()階
例如:
1.常數階
int sum=0,n=100; printf("hello word\n"); printf("hello word\n"); printf("hello word\n"); printf("hello word\n"); sum=(1+n)*n/2
所有常數項均可以看做是1,時間複雜度為O(1);
2.線性階:
含有非嵌套迴圈涉及線性階,就是隨著問題規模n的擴大,對應計算次數呈直線增長。
int i,n=100,sum=0; for(i=0;i<n;i++){ sum=sum+i; }
迴圈中的代碼需要執行n次,所以時間複雜度為O(n)
3.平方階:
int i,j,n=100; for(i=0;i<n;i++)
{ for(j=0;j<n;j++){ printf("hello word") } }
外層執行一次,內層執行100次,需要執行100*100次,n的平方次,所以時間複雜度為O(n^2),
如果有三個這樣的迴圈,則時間複雜度為O(n^3)
分析下,由於當i=0時,內迴圈執行了n次,當i=1時,內迴圈則執行n-1次.....當i=n-1時,內迴圈執行1次,所以總的執行次數應該是:- n+(n-1)+(n-2)+...+1 = n(n+1)/2,用我們推導大O的攻略,第一條忽略,因為沒有常數相加。第二條只保留最高項,所以n/2這項去掉。第三條,去除與最高項相乘的常數,最終得O(n^2)。
4.對數階
int i=1,n=100; while(i<n){ i=i*2; }
由於2^x=n得到x=log(2)n,所以這個迴圈的時間複雜度為O(log(2)n)
函數調用的時間複雜度分析:
例1:
int i,j; for(i=0;i<n;i++){ function(i); } void function(int count){ printf("%d",count); }
函數體是列印這個參數,function函數的時間複雜度是O(1),所以整體的時間複雜度就是迴圈的次數O(n)。
例2:
void function(int count){ int j; for(j=count;j<n;j++){ printf("%d",j); }
count++;
}
function內部的迴圈次數隨count的增加而減少,所以它的時間複雜度為O(n^2)。
例3:
n++; ##1 function(n);##一個內部迴圈的函數 O(N^2)
for(i=0;i<n;i++){ function(i);##內部迴圈的函數 } ## O(N^2) for(i=0;i<n;i++){ for(j=i;j<n;j++){ printf("%d",j); }}##O(n^2)
時間複雜度為O(n^2)
常見的時間複雜度:

常用時間複雜度所耗費的時間從小到大依次是:
O(1)<O(logn)<(n)<O(nlogn)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)
最壞情況與平均情況:
演算法的分析也是類似,我們查找一個有n個隨機數字數組中的某個數字,最好的情況是第一個數字就是,那麼演算法的時間複雜度為O(1),但也有可能這個數字就在最後一個位置,它的時間複雜度為O(n),平均運行時間是期望的運行時間,最壞的運行時間是一種保證,在應用中,這是一種最重要的需求,通常除非特別的指定,我們提到的運行時間都是最壞情況的運行時間。
演算法的空間複雜度:
演算法的空間複雜度通過計算演算法所需的存儲空間實現,演算法的空間複雜度的計算公式為:S(n)=O(f(n)),其中n為問題的規模,f(n)為語句關於n所占空間的函數。
一般情況"複雜度"指的是時間複雜度



