JavaScript圖形實例：曲線方程

来源:https://www.cnblogs.com/cs-whut/archive/2020/06/26/13193813.html
-Advertisement-
Play Games

在HTML5 Canvas畫布中，我們可以根據曲線的方程繪製出曲線。例如，在笛卡爾坐標系中，圓的方程為： x=r*cos(θ) y=r*sin(θ) （0≤θ≤2π） 編寫如下的HTML代碼。 <!DOCTYPE html> <head> <title>圓</title> <script type= ...


      在HTML5 Canvas畫布中，我們可以根據曲線的方程繪製出曲線。例如，在笛卡爾坐標系中，圓的方程為：

x=r*cos(θ)

y=r*sin(θ)     （0≤θ≤2π）

編寫如下的HTML代碼。

<!DOCTYPE html>

<head>

<title>圓</title>

<script type="text/javascript">

  function draw(id)

  {

     var canvas=document.getElementById(id);

     if (canvas==null)

        return false;

     var context=canvas.getContext('2d');

     context.fillStyle="#EEEEFF";

     context.fillRect(0,0,300,300);

     context.strokeStyle="red";

     context.lineWidth=2;

     context.save();

     context.translate(150,150);

     var  r=100;

     context.beginPath();

     for (theta=0;theta<=2*Math.PI;theta+=Math.PI/100)

     {

        var x = r*Math.cos(theta);       // 圓的方程式

        var y = r*Math.sin(theta);

        if (theta==0)

           context.moveTo(x,y);

        else

           context.lineTo(x,y);

      }

     context.stroke();

     context.restore();

   }

</script>

</head>

<body onload="draw('myCanvas');">

<canvas id="myCanvas" width="300" height="300"></canvas>

</body>

</html>

在瀏覽器中打開包含這段HTML代碼的html文件，可以看到在瀏覽器視窗中，繪製出一個圓心位於（150,150），半徑為100的圓。

若將HTML文件中的圓的方程改寫為：

        var x = 100*Math.cos(theta);     // 橢圓方程

        var y = 75*Math.sin(theta);

則在瀏覽器視窗中繪製出一個橢圓。

下麵我們給出採用曲線方程繪製的各類曲線實例。

1．星形線

星形線的笛卡爾坐標方程式為：

x=r*cos(θ)^3

y=r*sin(θ)^3       （0≤θ≤2π）

編寫如下的HTML代碼。

<!DOCTYPE html>

<head>

<title>星形線</title>

<script type="text/javascript">

  function draw(id)

  {

     var canvas=document.getElementById(id);

     if (canvas==null)

        return false;

     var context=canvas.getContext('2d');

     context.fillStyle="#EEEEFF";

     context.fillRect(0,0,300,300);

     context.strokeStyle="red";

     context.lineWidth=2;

     context.save();

     context.translate(150,150);

     var  r=80;

     context.beginPath();

     for (a=0;a<=2*Math.PI;a+=Math.PI/100)

     {

        var x = r*Math.cos(a)*Math.cos(a)*Math.cos(a);

        var y = r*Math.sin(a)*Math.sin(a)*Math.sin(a);

        if (a==0)

           context.moveTo(x,y);

        else

           context.lineTo(x,y);

      }

     context.stroke();

     context.restore();

   }

</script>

</head>

<body onload="draw('myCanvas');">

<canvas id="myCanvas" width="300" height="300"></canvas>

</body>

</html>

在瀏覽器中打開包含這段HTML代碼的html文件，可以看到在瀏覽器視窗中繪製出星形線，如圖1所示。

 

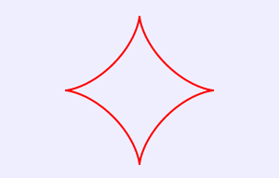
圖1  星形線

2．三尖瓣線

三尖瓣線的笛卡爾坐標方程式為：

x=r*[2*cos(θ)+ cos(2θ)]

y=r*[2*sin(θ)+ sin(2θ)]       （0≤θ≤2π）

編寫如下的HTML代碼。

<!DOCTYPE html>

<head>

<title>三尖瓣線</title>

<script type="text/javascript">

  function draw(id)

  {

     var canvas=document.getElementById(id);

     if (canvas==null)

        return false;

     var context=canvas.getContext('2d');

     context.fillStyle="#EEEEFF";

     context.fillRect(0,0,300,300);

     context.strokeStyle="red";

     context.lineWidth=2;

     context.save();

     context.translate(150,150);

     var  r=40;

     context.beginPath();

     for (a=0;a<=2*Math.PI;a+=Math.PI/100)

     {

        var x = r*(2*Math.cos(a)+Math.cos(2*a));

        var y = r*(2*Math.sin(a)-Math.sin(2*a));

        if (a==0)

           context.moveTo(x,y);

        else

           context.lineTo(x,y);

      }

     context.stroke();

     context.restore();

   }

</script>

</head>

<body onload="draw('myCanvas');">

<canvas id="myCanvas" width="300" height="300"></canvas>

</body>

</html>

在瀏覽器中打開包含這段HTML代碼的html文件，可以看到在瀏覽器視窗中繪製出三尖瓣線，如圖2所示。

  

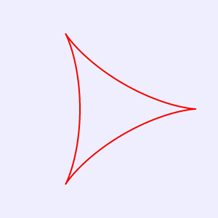
圖2  三尖瓣線

3．腎形線

腎形線的笛卡爾坐標方程式為：

x=r*[3*cos(θ)- cos(3θ)]

y=r*[3*sin(θ)- sin(3θ)]       （0≤θ≤2π）

編寫如下的HTML代碼。

<!DOCTYPE html>

<head>

<title>腎形線</title>

<script type="text/javascript">

  function draw(id)

  {

     var canvas=document.getElementById(id);

     if (canvas==null)

        return false;

     var context=canvas.getContext('2d');

     context.fillStyle="#EEEEFF";

     context.fillRect(0,0,300,300);

     context.strokeStyle="red";

     context.lineWidth=2;

     context.save();

     context.translate(150,150);

     var  r=25;

     context.beginPath();

     for (a=0;a<=2*Math.PI;a+=Math.PI/100)

     {

        var x = 3*r*Math.cos(a) -r*Math.cos(3*a);

        var y = 3*r*Math.sin(a) -r*Math.sin(3*a);

        if (a==0)

           context.moveTo(x,y);

        else

           context.lineTo(x,y);

      }

     context.stroke();

     context.restore();

   }

</script>

</head>

<body onload="draw('myCanvas');">

<canvas id="myCanvas" width="300" height="300"></canvas>

</body>

</html>

將上述HTML代碼保存到一個html文本文件中，再在瀏覽器中打開包含這段HTML代碼的html文件，可以看到在瀏覽器視窗中繪製出腎形線，如圖3所示。

  

圖3  腎形線

4．心臟線

心臟線的笛卡爾坐標方程式為：

    r=b*(1+ cos(θ))

x=r*cos(θ)

y=r*sin(θ)       （0≤θ≤2π）

編寫如下的HTML代碼。

<!DOCTYPE html>

<head>

<title>心臟線</title>

<script type="text/javascript">

  function draw(id)

  {

     var canvas=document.getElementById(id);

     if (canvas==null)

        return false;

     var context=canvas.getContext('2d');

     context.fillStyle="#EEEEFF";

     context.fillRect(0,0,300,300);

     context.strokeStyle="red";

     context.lineWidth=2;

     context.save();

     context.translate(100,150);

     var b=70;

     context.beginPath();

     for (theta=0;theta<=2*Math.PI;theta+=Math.PI/200)

     {

        var r=b*(1+Math.cos(theta));

        var x = r*Math.cos(theta);

        var y = r*Math.sin(theta);

        if (theta==0)

           context.moveTo(x,y);

        else

           context.lineTo(x,y);

      }

     context.stroke();

     context.restore();

   }

</script>

</head>

<body onload="draw('myCanvas');">

<canvas id="myCanvas" width="300" height="300"></canvas>

</body>

</html>

將上述HTML代碼保存到一個html文本文件中，再在瀏覽器中打開包含這段HTML代碼的html文件，可以看到在瀏覽器視窗中繪製出心臟線，如圖4所示。

  

圖4  心臟線

5．雙弧外擺線

雙弧外擺線的笛卡爾坐標方程式為：

x= 3*b*cos(θ)+ d*cos(3θ)]

y= 3*b*sin(θ)+ d*sin(3θ)]       （0≤θ≤2π）

編寫如下的HTML代碼。

<!DOCTYPE html>

<head>

<title>雙弧外擺線</title>

<script type="text/javascript">

  function draw(id)

  {

     var canvas=document.getElementById(id);

     if (canvas==null)

        return false;

     var context=canvas.getContext('2d');

     context.fillStyle="#EEEEFF";

     context.fillRect(0,0,300,300);

     context.strokeStyle="red";

     context.lineWidth=2;

     context.save();

     context.translate(150,150);

     var  b=25;

     var  d=35;

     context.beginPath();

     for (a=0;a<=2*Math.PI;a+=Math.PI/100)

     {

        var x = 3*b*Math.cos(a) +d*Math.cos(3*a);

        var y = 3*b*Math.sin(a) +d*Math.sin(3*a)

        if (a==0)

           context.moveTo(x,y);

        else

           context.lineTo(x,y);

      }

     context.stroke();

     context.restore();

   }

</script>

</head>

<body onload="draw('myCanvas');">

<canvas id="myCanvas" width="300" height="300"></canvas>

</body>

</html>

將上述HTML代碼保存到一個html文本文件中，再在瀏覽器中打開包含這段HTML代碼的html文件，可以看到在瀏覽器視窗中繪製出雙弧外擺線，如圖5所示。

  

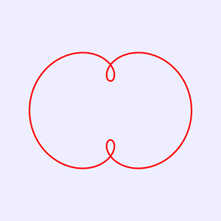
圖5  雙弧外擺線

6．梅花曲線

梅花曲線的笛卡爾坐標方程式為：

    r=10+(3*sin(θ*2.5))^2 

x=r*cos(θ)

y=r*sin(θ)              （0≤θ≤2π）

編寫如下的HTML代碼。

<!DOCTYPE html>

<head>

<title>梅花曲線</title>

<script type="text/javascript">

  function draw(id)

  {

     var canvas=document.getElementById(id);

     if (canvas==null)

        return false;

     var context=canvas.getContext('2d');

     context.fillStyle="#EEEEFF";

     context.fillRect(0,0,300,300);

     context.strokeStyle="red";

     context.lineWidth=2;

     context.save();

     context.translate(150,150);

     var b=120;

     context.beginPath();

     for (theta=0;theta<=2*Math.PI;theta+=Math.PI/200)

     {

        var r=10+9*Math.sin(2.5*theta)*Math.sin(2.5*theta);

        var x = 6*r*Math.cos(theta);

        var y = 6*r*Math.sin(theta);

        if (theta==0)

           context.moveTo(x,y);

        else

           context.lineTo(x,y);

      }

     context.stroke();

     context.restore();

   }

</script>

</head>

<body onload="draw('myCanvas');">

<canvas id="myCanvas" width="300" height="300"></canvas>

</body>

</html>

將上述HTML代碼保存到一個html文本文件中，再在瀏覽器中打開包含這段HTML代碼的html文件，可以看到在瀏覽器視窗中繪製出梅花曲線，如圖6所示。

  

圖6  梅花曲線

7．嚮日葵線

嚮日葵線的笛卡爾坐標方程式為：

    b=30

    r=b+b/3*sin(θ*b)  

x=r*cos(θ)

y=r*sin(θ)              （0≤θ≤2π）

編寫如下的HTML代碼。

<!DOCTYPE html>

<head>

<title>嚮日葵線</title>

<script type="text/javascript">

  function draw(id)

  {

     var canvas=document.getElementById(id);

     if (canvas==null)

        return false;

     var context=canvas.getContext('2d');

     context.fillStyle="#EEEEFF";

     context.fillRect(0,0,300,300);

     context.strokeStyle="red";

     context.lineWidth=2;

     context.save();

     context.translate(150,150);

     var b=30;

     context.beginPath();

     for (theta=0;theta<=2*Math.PI;theta+=Math.PI/200)

     {

        var r=b+b/3*Math.sin(b*theta);

        var x = 3*r*Math.cos(theta);

        var y = 3*r*Math.sin(theta);

        if (theta==0)

           context.moveTo(x,y);

        else

           context.lineTo(x,y);

      }

     context.stroke();

     context.restore();

   }

</script>

</head>

<body onload="draw('myCanvas');">

<canvas id="myCanvas" width="300" height="300"></canvas>

</body>

</html>

將上述HTML代碼保存到一個html文本文件中，再在瀏覽器中打開包含這段HTML代碼的html文件，可以看到在瀏覽器視窗中繪製出嚮日葵線，如圖7所示。

 

圖7  嚮日葵線

8．小蜜蜂形線

小蜜蜂形線的笛卡爾坐標方程式為：

x=r*[cos(θ)+ cos(3θ)]

y=r*[sin(θ)+ sin(5θ)]       （0≤θ≤2π）

編寫如下的HTML代碼。

<!DOCTYPE html>

<head>

<title>小蜜蜂形線</title>

<script type="text/javascript">

  function draw(id)

  {

     var canvas=document.getElementById(id);

     if (canvas==null)

        return false;

     var context=canvas.getContext('2d');

     context.fillStyle="#EEEEFF";

     context.fillRect(0,0,300,300);

     context.strokeStyle="red";

     context.lineWidth=2;

     context.save();

     context.translate(150,150);

     var r=50;

     context.beginPath();

     for (theta=0;theta<=2*Math.PI;theta+=Math.PI/100)

     {

        var x = r*(Math.cos(theta)+Math.cos(3*theta));

        var y = r*(Math.sin(theta)+Math.sin(5*theta));

        if (theta==0)

           context.moveTo(x,y);

        else

           context.lineTo(x,y);

      }

     context.stroke();

     context.restore();

   }

</script>

</head>

<body onload="draw('myCanvas');">

<canvas id="myCanvas" width="300" height="300"></canvas>

</body>

</html>

將上述HTML代碼保存到一個html文本文件中，再在瀏覽器中打開包含這段HTML代碼的html文件，可以看到在瀏覽器視窗中繪製出小蜜蜂形線，如圖8所示。

  

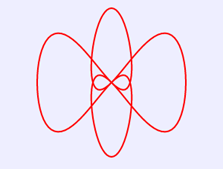
圖8 小蜜蜂形線

9．彎月

彎月的笛卡爾坐標方程式為：

x=r*[cos(θ)+ cos(2θ)]

y=r*4*sin(θ)       （0≤θ≤2π）

編寫如下的HTML代碼。

<!DOCTYPE html>

<head>

<title>彎月</title>

<script type="text/javascript">

  function draw(id)

  {

     var canvas=document.getElementById(id);

     if (canvas==null)

        return false;

     var context=canvas.getContext('2d');

     context.fillStyle="#EEEEFF";

     context.fillRect(0,0,300,300);

     context.strokeStyle="red";

     context.lineWidth=2;

     context.save();

     context.translate(150,150);

     var r=30;

     context.beginPath();

     for (theta=0;theta<=2*Math.PI;theta+=Math.PI/100)

     {

        var x = r*(Math.cos(theta)+Math.cos(2*theta));

        var y = r*(Math.sin(theta)*4);

        if (theta==0)

           context.moveTo(x,y);

        else

           context.lineTo(x,y);

      }

     context.stroke();

     context.restore();

   }

</script>

</head>

<body onload="draw('myCanvas');">

<canvas id="myCanvas" width="300" height="300"></canvas>

</body>

</html>

將上述HTML代碼保存到一個html文本文件中，再在瀏覽器中打開包含這段HTML代碼的html文件，可以看到在瀏覽器視窗中繪製出彎月，如圖9所示。

  

圖9  彎月

10．內五角星線

內五角星線的笛卡爾坐標方程式為：

    b=10;

    x = b*(2+5* cos(θ)+6* cos((10/6-1)* θ));

    y = b*(2+5* sin(θ)-6* sin((10/6-1)* θ));    （0≤θ≤14π）

編寫如下的HTML代碼。

<!DOCTYPE html>

<head>

<title>內五角星線</title>

<script type="text/javascript">

  function draw(id)

  {

     var canvas=document.getElementById(id);

     if (canvas==null)

        return false;

     var context=canvas.getContext('2d');

     context.fillStyle="#EEEEFF";

     context.fillRect(0,0,300,300);

     context.strokeStyle="red";

     context.lineWidth=2;

     context.save();

     context.translate(150,150);

     var  b=10;

     context.beginPath();

     for (a=0;a<=14*Math.PI;a+=Math.PI/100)

     {

        var x = b*(2+5*Math.cos(a)+6*Math.cos((10/6-1)*a));

        var y = b*(2+5*Math.sin(a)-6*Math.sin((10/6-1)*a));

        if (a==0)

           context.moveTo(x,y);

        else

           context.lineTo(x,y);

      }

     context.stroke();

     context.restore();

   }

</script>

</head>

<body onload="draw('myCanvas');">

<canvas id="myCanvas" width="300" height="300"></canvas>

</body>

</html>

將上述HTML代碼保存到一個html文本文件中，再在瀏覽器中打開包含這段HTML代碼的html文件，可以看到在瀏覽器視窗中繪製出內五角星線，如圖10所示。

 

圖10  內五角星線

11．熱帶魚形線

熱帶魚形線的笛卡爾坐標方程式為：

    x =( r* cos(3θ)^4)* θ;

    y = ( r* sin(3θ)^4)* θ;    （0≤θ≤2π）

編寫如下的HTML代碼。

<!DOCTYPE html>

<head>

<title>熱帶魚形線</title>

<script type="text/javascript">

  function draw(id)

  {

     var canvas=document.getElementById(id);

     if (canvas==null)

        return false;

     var context=canvas.getContext('2d');

     context.fillStyle="#EEEEFF";

     context.fillRect(0,0,300,300);

     context.strokeStyle="red";

     context.lineWidth=2;

     context.save();

     context.translate(30,30);

     var r=45;

     context.beginPath();

     for (theta=0;theta<=2*Math.PI;theta+=Math.PI/100)

     {

        x= (r*Math.cos(3*theta)*Math.cos(3*theta)*Math.cos(3*theta)*Math.cos(3*theta))*theta;

        y= (r*Math.sin(3*theta)*Math.sin(3*theta)*Math.sin(3*theta)*Math.sin(3*theta))*theta;

        if (theta==0)

           context.moveTo(x,y);

        else

           context.lineTo(x,y);

      }

     context.stroke();

     context.restore();

   }

</script>

</head>

<body onload="draw('myCanvas');">

<canvas id="myCanvas" width="300" height="300"></canvas>

</body>

</html>

將上述HTML代碼保存到一個html文本文件中，再在瀏覽器中打開包含這段HTML代碼的html文件，可以看到在瀏覽器視窗中繪製出熱帶魚形線，如圖11所示。

  

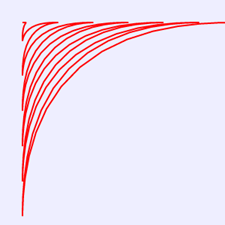
圖11  熱帶魚形線

12．蝸軌線

蝸軌線的笛卡爾坐標方程式為：

    r=cos(30*θ) *θ/2+2*θ 

x=r*cos(θ)

y=r*sin(θ)              （0≤θ≤4π）

編寫如下的HTML代碼。

<!DOCTYPE html>

<head>

<title>蝸軌線</title>

<script type="text/javascript">

  function draw(id)

  {

     var canvas=document.getElementById(id);

     if (canvas==null)

        return false;

     var context=canvas.getContext('2d');

     context.fillStyle="#EEEEFF";

     context.fillRect(0,0,400,300);

     context.strokeStyle="red";

     context.lineWidth=2;

     context.save();

     context.translate(150,150);

     context.beginPath();

     for (theta=0;theta<=4*Math.PI;theta+=Math.PI/720)

     {

        var r=Math.cos(30*theta)*theta*0.5+theta*2;

        var x = 5*r*Math.cos(theta);

        var y = 5*r*Math.sin(theta);

        if (theta==0)

           context.moveTo(x,y);

        else

           context.lineTo(x,y);

      }

     context.stroke();

     context.restore();

   }

</script>

</head>

<body onload="draw('myCanvas');">

<canvas id="myCanvas" width="400" height="300"></canvas>

</body>

</html>

將上述HTML代碼保存到一個html文本文件中，再在瀏覽器中打開包含這段HTML代碼的html文件，可以看到在瀏覽器視窗中繪製出蝸軌線，如圖12所示。

  

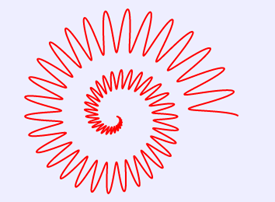
圖12  蝸軌線

13．蝴蝶曲線

蝴蝶曲線的笛卡爾坐標方程式為：

    r=(cos(2*θ) *θ/2+1) *θ 

x=r*cos(θ)

y=r*sin(θ)              （0≤θ≤15π）

編寫如下的HTML代碼。

<!DOCTYPE html>

<head>

<title>蝴蝶曲線</title>

<script type="text/javascript">

  function draw(id)

  {

     var canvas=document.getElementById(id);

     if (canvas==null)

        return false;

     var context=canvas.getContext('2d');

     context.fillStyle="#EEEEFF";

     context.fillRect(0,0,400,300);

     context.strokeStyle="red";

     context.lineWidth=2;

     context.save();

     context.translate(200,150);

     context.beginPath();

     for (theta=0;theta<=15*Math.PI;theta+=Math.PI/180)

     {

        var r=(Math.cos(2*theta)*theta*0.5+1)*theta;

        var x = 0.15*r*Math.cos(theta);

        var y = 0.15*r*Math.sin(theta);

        if (theta==0)

           context.moveTo(x,y);

        else

           context.lineTo(x,y);

      }

     context.stroke();

     context.restore();

   }

</script>

</head>

<body onload="draw('myCanvas');">

<canvas id="myCanvas" width="400" height="300"></canvas>

</body>

</html>

將上述HTML代碼保存到一個html文本文件中，再在瀏覽器中打開包含這段HTML代碼的html文件，可以看到在瀏覽器視窗中繪製出蝴蝶曲線，如圖13所示。

  

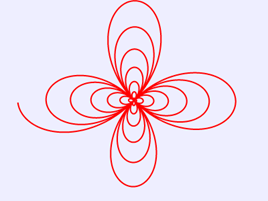
圖13  蝴蝶曲線

14．長短幅圓內旋輪線

長短幅圓內旋輪線的笛卡爾坐標方程式為：

    x =(a-b)* cos(θ)+c* cos((a/b-1)*θ);

    y =(a-b)* sin(θ) - c* sin((a/b-1)*θ);    （0≤θ≤20π）

編寫如下的HTML代碼。

<!DOCTYPE html>

<head>

<title>長短幅圓內旋輪線</title>

<script type="text/javascript">

  function draw(id)

  {

     var canvas=document.getElementById(id);

     if (canvas==null)

        return false;

     var context=canvas.getContext('2d');

     context.fillStyle="#EEEEFF";

     context.fillRect(0,0,300,300);

     context.strokeStyle="red";

     context.lineWidth=2;

     context.save();

     context.translate(150,150);

     var a=100;

     var b=140;

     var c=45;

     context.beginPath();

     for (theta=0;theta<=20*Math.PI;theta+=Math.PI/100)

     {

        var x = (a-b)*Math.cos(theta)+c*Math.cos((a/b-1)*theta);

        var y = (a-b)*Math.sin(theta)-c*Math.sin((a/b-1)*theta);

        if (theta==0)

           context.moveTo(x,y);

        else

           context.lineTo(x,y);

      }

     context.stroke();

     context.restore();

   }

</script>

</head>

<body onload="draw('myCanvas');">

<canvas id="myCanvas" width="300" height="300"></canvas>

</body>

</html>

將上述HTML代碼保存到一個html文本文件中，再在瀏覽器中打開包含這段HTML代碼的html文件，可以看到在瀏覽器視窗中繪製出長短幅圓內旋輪線，如圖14所示。

  

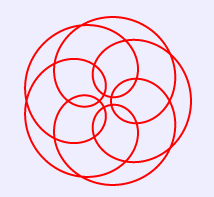
圖14  長短幅圓內旋輪線

15．長短幅圓外旋輪線

長短幅圓外旋輪線的笛卡爾坐標方程式為：

    x =(a+b)* cos(θ)+c* cos((a/b+1)*θ);

    y =(a+b)* sin(θ) - c* sin((a/b+1)*θ);    （0≤θ≤10π）

編寫如下的HTML代碼。

<!DOCTYPE html>

<head>

<title>長短幅圓外旋輪線</title>

<script type="text/javascript">

  function draw(id)

  {

     var canvas=document.getElementById(id);

     if (canvas==null)

        return false;

     var context=canvas.getContext('2d');

     context.fillStyle="#EEEEFF";

     context.fillRect(0,0,300,300);

     context.strokeStyle="red";

     context.lineWidth=2;

     context.save();

     context.translate(150,150);

     var a=50;

     var b=30;

     var c=50;

     context.beginPath();

     for (theta=0;theta<=10*Math.PI;theta+=Math.PI/100)

     {

        var x = (a+b)*Math.cos(theta)+c*Math.cos((a/b+1)*theta);

        var y = (a+b)*Math.sin(theta)-c*Math.sin((a/b+1)*theta);

        if (theta==0)

           context.moveTo(x,y);

        else

           context.lineTo(x,y);

      }

     context.stroke();

     context.restore();

   }

</script>

</head>

<body onload="draw('myCanvas');">

<canvas id="myCanvas" width="300" height="300"></canvas>

</body>

</html>

將上述HTML代碼保存到一個html文本文件中，再在瀏覽器中打開包含這段HTML代碼的html文件，可以看到在瀏覽器視窗中繪製出長短幅圓外旋輪線，如圖15所示。

  

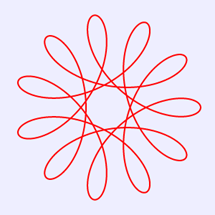
圖15  長短幅圓外旋輪線


您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • 表單及其控制項的瞭解
    瞭解表單及其控制項 1.form:表單標簽 表單屬性： action:表單提交到哪裡 method:以什麼方式去提交到action指定的地址，有get和post,預設為get target: placeholder:表示在文本裡面預設顯示什麼文字 2.form裡面含有的控制項： input: selec ...
  • JavaScript：計算時間及倒計時
    var start = "2020-6-26 20:36:00"; //開始時間 var now = new Date(); //當前時間 var ns = new Date(start).getTime() - now.getTime(); //毫秒差 //時間差 var todays = fun ...
  • JS-多關鍵詞列表高亮
    /** * 多個關鍵詞列表高亮(word_list1,color1,word_list2,color2,...) * @param word_list 關鍵詞列表(例: ["關鍵詞a","關鍵詞b"],不區分大小寫) * @param color 顏色值(例: "#ff0000") * @retur ...
  • 9.普利姆演算法求最小生成樹（JavaScript版）
    普利姆演算法（加點法）求最小生成樹 <!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8"> <meta name="viewport" content="width=device-width, initial-scale=1.0"> ...
  • vue~父組件與子組件的交互
    我們在進行vue開發時會將公共的部分進行抽象，然後生成一個獨立的組件，這個組件可以被其它頁面引用，如果希望有交互的動作就設計到了值的傳遞，或者方法的回調等問題，這一次我們主要來說一下父組件和子組件的交互。 值的傳遞 子組件，通過定義了prods，然後可以實現從父組件向子組件的傳遞： <templat ...
  • 手摸手帶你理解Vue的Computed原理
    前言 computed 在 Vue 中是很常用的屬性配置，它能夠隨著依賴屬性的變化而變化，為我們帶來很大便利。那麼本文就來帶大家全面理解 computed 的內部原理以及工作流程。 在這之前，希望你能夠對響應式原理有一些理解，因為 computed 是基於響應式原理進行工作。如果你對響應式原理還不是 ...
  • JavaScript圖形實例：利用插值實現圖像漸變
    描述由一個圖形變化為另一個圖形過程中的各個中間圖形，稱為漸變圖形。可以利用插值演算法求得各個漸變圖形。 設在源圖形和目標圖形上各取M個對應坐標點，並分別保存到數組中，源圖形用數組SX[M]和SY[M]保存M個坐標點（sx，sy），目標圖形用數組DX[M]和DY[M]保存M個坐標點（dx，dy）。若需生 ...
  • JavaScript圖形實例：再談曲線方程
    在“JavaScript圖形實例：曲線方程”一文中，我們給出了15個曲線方程繪製圖形的實例。在本文中，我們繼續討論一下曲線方程。在本文中，我們討論的方法時，先給出一個繪製特定圖案的曲線方程，然後將方程中的一些取值參數化，然後看看這些參數取不同值時會繪製出怎樣的圖形，從而通過試探加猜測的方式找出一些繪 ...
一周排行
    -Advertisement-
    Play Games
  • 移動開發（一）：使用.NET MAUI開發第一個安卓APP
    移動開發（一）：使用.NET MAUI開發第一個安卓APP 對於工作多年的C#程式員來說，近來想嘗試開發一款安卓APP，考慮了很久最終選擇使用.NET MAUI這個微軟官方的框架來嘗試體驗開發安卓APP，畢竟是使用Visual Studio開發工具，使用起來也比較的順手，結合微軟官方的教程進行了安卓 ...
  • wpf ToggleButton選中效果和一個登錄界面
    前言 QuestPDF 是一個開源 .NET 庫，用於生成 PDF 文檔。使用了C# Fluent API方式可簡化開發、減少錯誤並提高工作效率。利用它可以輕鬆生成 PDF 報告、發票、導出文件等。 項目介紹 QuestPDF 是一個革命性的開源 .NET 庫，它徹底改變了我們生成 PDF 文檔的方 ...
  • 彈幕樹洞項目功能新增篇
    項目地址 項目後端地址： https://github.com/ZyPLJ/ZYTteeHole 項目前端頁面地址： ZyPLJ/TreeHoleVue (github.com) https://github.com/ZyPLJ/TreeHoleVue 目前項目測試訪問地址： http://tree ...
  • 第27篇 sqlserver2022詳細安裝步驟
    話不多說，直接開乾 一.下載 1.官方鏈接下載： https://www.microsoft.com/zh-cn/sql-server/sql-server-downloads 2.在下載目錄中找到下麵這個小的安裝包 SQL2022-SSEI-Dev.exe，運行開始下載SQL server； 二. ...
  • .NET 開源高性能 MQTT 類庫
    前言 隨著物聯網（IoT）技術的迅猛發展，MQTT（消息隊列遙測傳輸）協議憑藉其輕量級和高效性，已成為眾多物聯網應用的首選通信標準。 MQTTnet 作為一個高性能的 .NET 開源庫，為 .NET 平臺上的 MQTT 客戶端與伺服器開發提供了強大的支持。 本文將全面介紹 MQTTnet 的核心功能 ...
  • Serilog文檔翻譯系列（六） - 可用的接收器、增強器、格式化輸出
    Serilog支持多種接收器用於日誌存儲，增強器用於添加屬性，LogContext管理動態屬性，支持多種輸出格式包括純文本、JSON及ExpressionTemplate。還提供了自定義格式化選項，適用於不同需求。 ...
  • 警惕 Visual Studio 屬性求值副作用導致邏輯不符合預期
    目錄簡介獲取 HTML 文檔解析 HTML 文檔測試參考文章 簡介 動態內容網站使用 JavaScript 腳本動態檢索和渲染數據，爬取信息時需要模擬瀏覽器行為，否則獲取到的源碼基本是空的。 本文使用的爬取步驟如下： 使用 Selenium 獲取渲染後的 HTML 文檔 使用 HtmlAgility ...
  • [使用目前最新版]HybridCLR6.9.0+YooAsset2.2.4實現純C# Unity熱更新方案 (一)
    1.前言 什麼是熱更新 游戲或者軟體更新時，無需重新下載客戶端進行安裝，而是在應用程式啟動的情況下，在內部進行資源或者代碼更新 Unity目前常用熱更新解決方案 HybridCLR，Xlua，ILRuntime等 Unity目前常用資源管理解決方案 AssetBundles，Addressable， ...
  • 在 ASP.NET Core Web API 中使用操作篩選器統一處理通用操作
    本文章主要是在C# ASP.NET Core Web API框架實現向手機發送驗證碼簡訊功能。這裡我選擇是一個互億無線簡訊驗證碼平臺，其實像阿裡雲，騰訊雲上面也可以。 首先我們先去 互億無線 https://www.ihuyi.com/api/sms.html 去註冊一個賬號 註冊完成賬號後，它會送 ...
  • 第28篇 如何.net中實現高效可靠數據同步api
    通過以下方式可以高效，並保證數據同步的可靠性 1.API設計 使用RESTful設計，確保API端點明確，並使用適當的HTTP方法（如POST用於創建，PUT用於更新）。 設計清晰的請求和響應模型，以確保客戶端能夠理解預期格式。 2.數據驗證 在伺服器端進行嚴格的數據驗證，確保接收到的數據符合預期格 ...
所有分類