什麼是監督學習？什麼是無監督學習？監督學習：有目標y值，如線性回歸，分類演算法無監督學習：無目標y值，如聚類邏輯回歸是分類演算法，不要被名字誤導，得到的是離散值引入邏輯回歸邏輯回歸主要用於二分類線上性回歸中:Y=W1X1+W2X2+W3X3 +...+b=WT*X 在邏輯回歸中，習慣用Z表示 ...

什麼是監督學習？什麼是無監督學習？

監督學習：有目標y值，如線性回歸，分類演算法無監督學習：無目標y值，如聚類邏輯回歸是分類演算法，不要被名字誤導，得到的是離散值

引入邏輯回歸

邏輯回歸主要用於二分類

線上性回歸中:Y=W1X1+W2X2+W3X3 +...+b=W^T*X 在邏輯回歸中，習慣用Z表示，Z=W1X1+W2X2+W3X3 +...+b=W^T*X 邏輯回歸線上性回歸的基礎上，將每條樣本打分，然後設置一個閾值，分為一個類別，而沒有達到這個閾值的分位另一個類別習慣上，我們用0，1表示不同類別0為負例，1位正例。 Z取值（-∞，+∞）：當Z>0表示正例1；　　　　　　　　　當Z<=0，表示負例0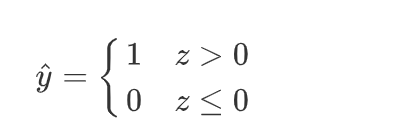

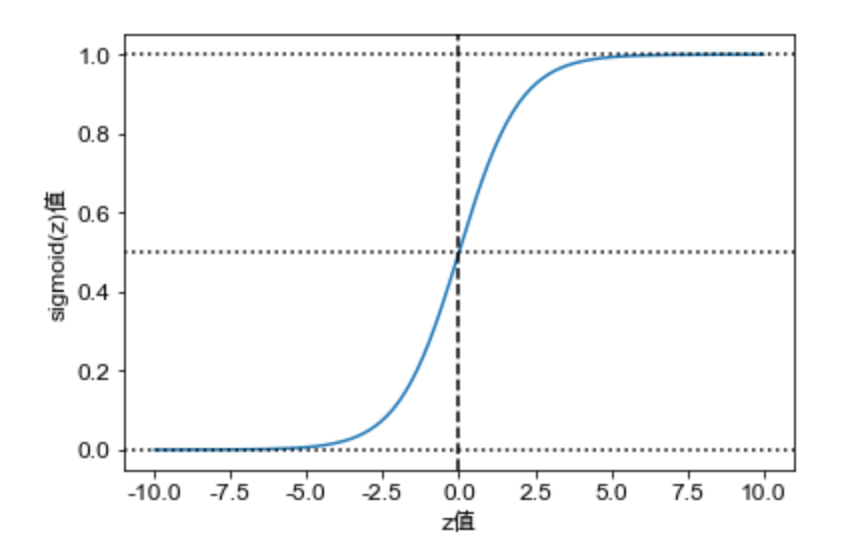
為了將Z值轉換為有界的概率值，我們引入sigmoid函數。

sigmoid函數

sigmoid函數也叫S型函數

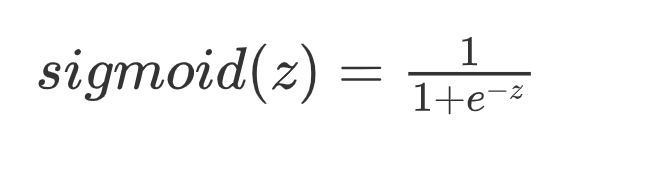
當z=0時，p=sigmoid(z)=0.5，因此上式y預測值還可表示為

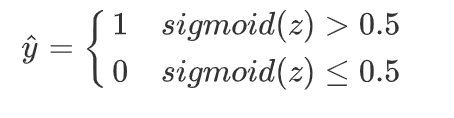
轉為概率：

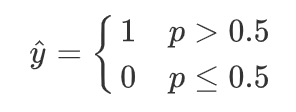
圖形為：

計算時，正例的概率為sigmoid(z),負例的概率為1-sigmoid(z).

樣本概率：p(y=1|x;w)=S(z)

　　　　　p(y=0|x;w)=1-S(z)

w的含義：以w作為參數

兩式子綜合即一個樣本的概率：p(y|x;w)=S(z)^y(1-S(z))^1-y

那麼要求解能夠使所有樣本聯合概率密度最大的w值，根據最大似然估計，所有樣本的聯合概率密度函數（似然函數）為：

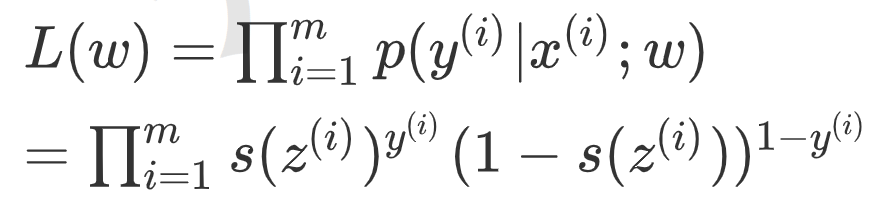
左右取對數：

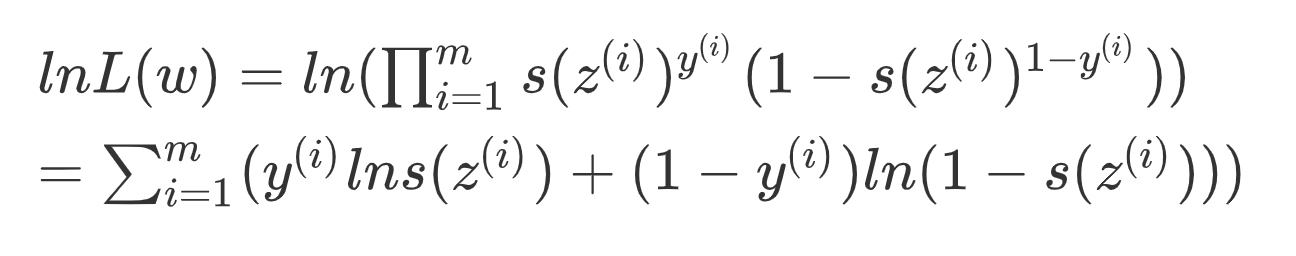
上式最大即相反數最小，引入損失函數

邏輯回歸的損失函數（對數損失函數）

可採用梯度下降求解參數w,即對w求偏導

除以m這一因數並不改變最終求導極值結果，通過除以m可以得到平均損失值，避免樣本數量對於損失值的影響

下圖用θ表示w：

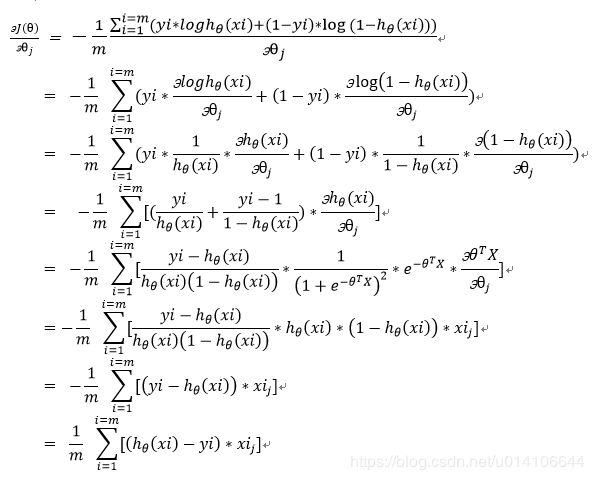
對數損失函數來歷總結：樣本概率-->聯合概率密度--> 取對數-->取相反數

損失函數與sigmoid的關係

當數據為類別1時，我們應當讓的值儘可能大，反之，當數據為類別0時，我們應當讓的值儘可能小，即1 - 的值儘可能大

當數據為類別1時，我們應當讓sigmoid(z)的值儘可能大，損失值儘可能小，得到的預測結果與目標結果儘可能接近；反之，當數據為類別0時，我們應當讓sigmoid(z)的值儘可能小，（即1 -sigmoid(z)的值儘可能大），損失值也儘可能的小，預測結果與目標結果越接近。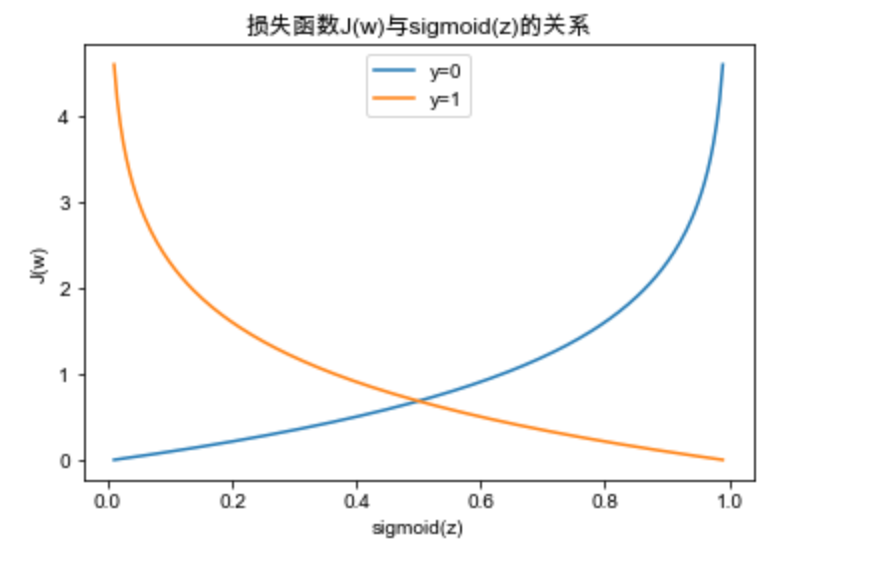

邏輯回歸實現二分類

以下以鳶尾花數據集為例

# LogisticRegression:邏輯回歸的類
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
import warnings

warnings.filterwarnings("ignore")

iris = load_iris()
X, y = iris.data, iris.target
# 因為鳶尾花具有三個類別(y=0，1，2)，4個特征(列)，此處僅使用其中兩個特征，並且移除一個類別（類別0）。
X = X[y != 0, 2:]
y = y[y != 0]
# 此時，y的標簽為1與2，我們這裡將其改成0與1。（僅僅是為了習慣而已）
y[y == 1] = 0
y[y == 2] = 1
# 切分訓練集跟測試集 
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=2)
# 創建邏輯回歸對象
lr = LogisticRegression()
# 訓練集進行訓練 確定w和b的值
lr.fit(X_train, y_train)
# 將測試集放到模型中得到預測的結果
y_hat = lr.predict(X_test)
print("權重：", lr.coef_)
print("偏置：", lr.intercept_)
print("真實值：", y_test)
print("預測值：", y_hat)

對分類結果進行可視化

# 對分類的結果進行可視化
c1 = X[y == 0]
c2 = X[y == 1]
plt.scatter(x=c1[:, 0], y=c1[:, 1], c="g", label="類別0")
plt.scatter(x=c2[:, 0], y=c2[:, 1], c="r", label="類別1")
plt.xlabel("花瓣長度")
plt.ylabel("花瓣寬度")
plt.title("鳶尾花樣本分佈")
plt.legend()

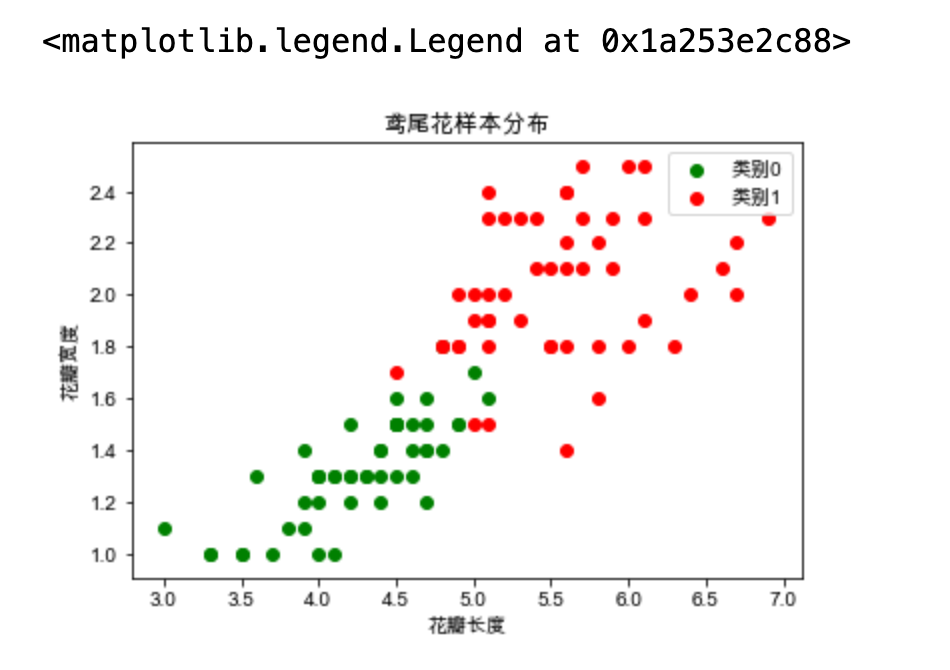
對分類結果進行可視化

# 對分類的結果進行可視化
c1 = X[y == 0]
c2 = X[y == 1]
plt.scatter(x=c1[:, 0], y=c1[:, 1], c="g", label="類別0")
plt.scatter(x=c2[:, 0], y=c2[:, 1], c="r", label="類別1")
plt.xlabel("花瓣長度")
plt.ylabel("花瓣寬度")
plt.title("鳶尾花樣本分佈")
plt.legend()

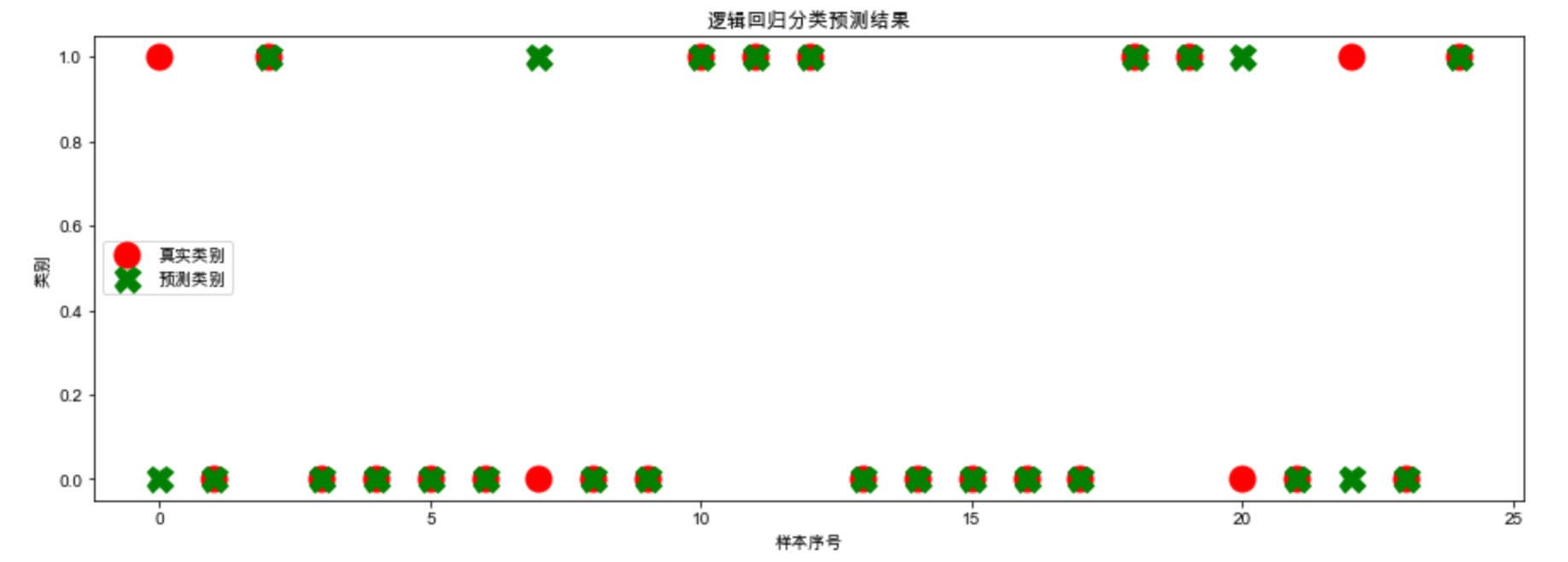
樣本的真實類別與預測類別

plt.figure(figsize=(15, 5))
plt.plot(y_test, marker="o", ls="", ms=15, c="r", label="真實類別")
plt.plot(y_hat, marker="X", ls="", ms=15, c="g", label="預測類別")
plt.legend()
plt.xlabel("樣本序號")
plt.ylabel("類別")
plt.title("邏輯回歸分類預測結果")
plt.show()

計算概率值

# 打分
# 獲取預測的概率值，包含數據屬於每個類別的概率。返回的概率是通過sigmoid函數計算的(二分類下 )
probability = lr.predict_proba(X_test)

# 展示前五行數據的概率值
display(probability[:5])
# 從索引的角度查看最大值,axis=1：只看列索引 
display(np.argmax(probability, axis=1))
# 產生序號，用於可視化的橫坐標。
index = np.arange(len(X_test))
# 提取0，1的概率
pro_0 = probability[:, 0]
pro_1 = probability[:, 1]
tick_label = np.where(y_test == y_hat, "O", "X")
plt.figure(figsize=(15, 5))

# 繪製堆疊圖
plt.bar(index, height=pro_0, color="g", label="類別0概率值")
# bottom=x，表示從x的值開始堆疊上去。
# tick_label 設置標簽刻度的文本內容。
plt.bar(index, height=pro_1, color='r', bottom=pro_0, label="類別1概率值", tick_label=tick_label)
# 圖例位置可試著調整，放在圖外
plt.legend(loc="best", bbox_to_anchor=(1, 1))
plt.xlabel("樣本序號")
plt.ylabel("各個類別的概率")
plt.title("邏輯回歸分類概率")
plt.show()

模型lr.predict_proba方法返回的概率：會返回屬於樣本的每一個概率；是通過sigmoid(z)函數計算的（二分類下）。

繪製決策邊界

# 繪製決策邊界

# 傳入顏色
from matplotlib.colors import ListedColormap

# 定義函數，用於繪製決策邊界。
# model：模型 比如邏輯回歸模型
# X：傳入的數據集 （樣本集）
# y:傳入的類別
def plot_decision_boundary(model, X, y):
    # 定義了三種顏色和標記
    color = ["r", "g", "b"]
    marker = ["o", "v", "x"]
    # y一共有幾個類別 這裡只有0，1
    class_label = np.unique(y)
    # ListedColormap定義不同的顏色圖  
    # len ：有幾個類別取幾個顏色
    cmap = ListedColormap(color[: len(class_label)])
    # x1和x2取不同的值 進行笛卡爾積
    x1_min, x2_min = np.min(X, axis=0)
    x1_max, x2_max = np.max(X, axis=0)
    # 在最小最大值的基礎上加減1是為了繪圖時不在邊界上，取值間隔為0.02
    x1 = np.arange(x1_min - 1, x1_max + 1, 0.02)
    x2 = np.arange(x2_min - 1, x2_max + 1, 0.02)
    # 擴展x1,x2以便meshgrid生成笛卡爾積 x1行擴展，x2列擴展 （想象成坐標格子）
    X1, X2 = np.meshgrid(x1, x2)
    # print("X1:{}\nX2:{}".format(X1,X2))
    # ravel把二維的X1 X2 拉成一維
    # Z的形狀要跟X1的形狀一致 Z為預測值0，1
    Z = model.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape)
    # print("Z:",Z[0:5,:])
    # contourf繪製使用顏色填充的等高線。--不同的值畫不同的顏色 畫底板顏色
    # X1, X2, Z的形狀必須相同
    # alpha=0.5給一個透明度 讓樣本看得見
    plt.contourf(X1, X2, Z, cmap=cmap, alpha=0.5)
    # enumerate 函數用於遍歷序列中的元素以及它們的下標：返回index，value  
    # 繪製樣本顏色 一共兩種顏色 一次性先繪製為0的顏色，再繪製為1的顏色
    for i, class_ in enumerate(class_label):
        # print("i:",i)
        # print("class_:",class_)
        plt.scatter(x=X[y == class_, 0], y=X[y == class_, 1], 
                c=cmap.colors[i], label=class_, marker=marker[i])
    plt.legend()
    plt.show()

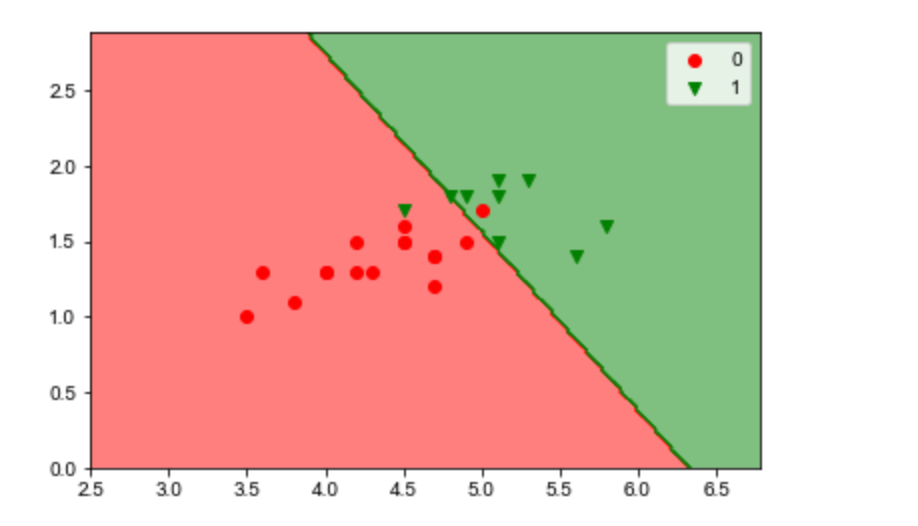
訓練集的劃分效果

# 訓練集的劃分效果
plot_decision_boundary(lr, X_train, y_train)
# 決策邊界的幾何意義：W*X=0就是那條決策線，>0就劃分為1，<0就劃分為0

訓練集的劃分效果

# 測試集的劃分效果
plot_decision_boundary(lr, X_test, y_test)

邏輯回歸實現多分類

# 邏輯回歸實現多分類 是指y值有多個類
# 不把y==2的值踢出去
iris = load_iris()
X, y = iris.data, iris.target
# 僅使用其中的兩個特征。
X = X[:, 2:]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=0)
# sklearn中不同版本預設值可能不一樣  
# multi_class參數，從0.22版本起，預設值從“ovr”變成“auto”。auto的意思為自動選擇，如果是二分類，就使用ovr，如果是多分類，就使用“multinomial”。
# solver參數，從0.22版本起，預設值由“liblinear”改為“lbfgs”。solver控制的是優化策略，也就是求解參數w時候的優化方案。
 # 第一種 二分類
# lr = LogisticRegression(multi_class="ovr", solver="liblinear")
# 第二種 n分類(n>2)
# lr = LogisticRegression(multi_class="multinomial", solver="lbfgs")
lr = LogisticRegression()
lr.fit(X_train, y_train)
y_hat = lr.predict(X_test)
print("分類正確率：", np.sum(y_test == y_hat) / len(y_test))

分類正確率： 0.9736842105263158

訓練集決策邊界

# 訓練集決策邊界
plot_decision_boundary(lr, X_train, y_train)

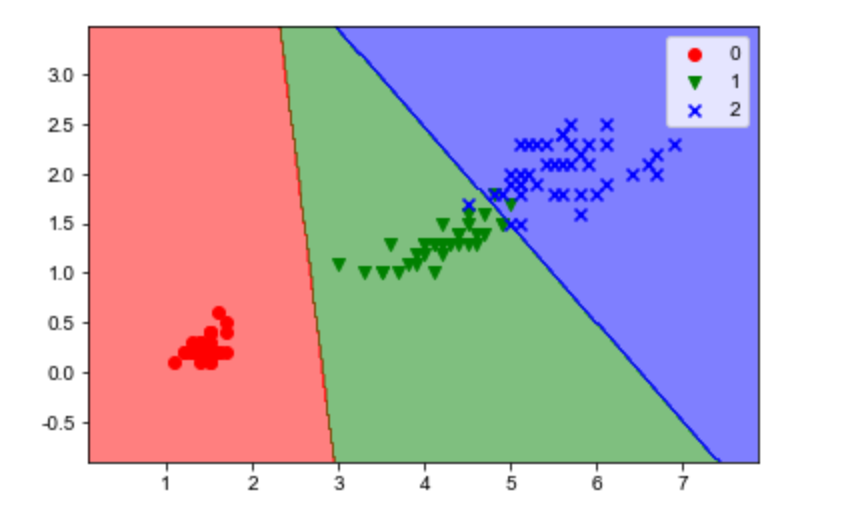
測試集決策邊界

plot_decision_boundary(lr, X_test, y_test)

補充

用於多分類的還有：

多項式（multinomial）：z有正有負，用ez,它一定大於0，技巧：e^z₁/( e^z1₊ e^z₂₊ez₃)
一對多（one versus rest） A B C ,是A，不是A；是B，不是B；是C，不是C。

完結散花

參考文獻：https://blog.csdn.net/u014106644/article/details/83660226，開課吧

機器學習之邏輯回歸