順序查找:就是從第一個元素開始,按索引順序遍歷待查找序列,直到找出給定目標或者查找失敗 缺點:效率低 -- 需要遍歷整個待查序列 二分法查找:也稱為折半法,是一種在有序數組中查找特定元素的搜索演算法。 1:首先,從數組的中間元素開始搜索,如果該元素正好是目標元素,則搜索過程結束,否則執行下一步。 2: ...
順序查找:就是從第一個元素開始,按索引順序遍歷待查找序列,直到找出給定目標或者查找失敗
缺點:效率低 -- 需要遍歷整個待查序列
二分法查找:也稱為折半法,是一種在有序數組中查找特定元素的搜索演算法。
1:首先,從數組的中間元素開始搜索,如果該元素正好是目標元素,則搜索過程結束,否則執行下一步。
2:如果目標元素大於/小於中間元素,則在數組大於/小於中間元素的那一半區域查找,然後重覆步驟1的操作。
3:如果某一步數組為空,則表示找不到目標元素
樹的概念
樹:連通無迴路的無向圖是一棵樹.
根:樹中的根是樹的一個節點,任意節點都可以為根,根據不同問題可以選擇樹的一個頂點為根.
子節點&父節點:樹根為0層,直接和樹根相連的節點為根節點的子節點,根節點為其父節點,根節點的子節點為樹的1層.對於除了根節點以外的節點u來說,直接與其相連的節點中,除了一個父節點以外的所有節點都是u的子節點,u節點的子節點的層數為u節點的層數加1.
子樹:對於樹中的一個節點u來說,包含其一個兒子節點以及兒子節點的所有後輩節點的樹稱為節點u的子樹.
兄弟節點:同一父節點的子節點.
葉子節點:沒有子節點的節點稱為葉子節點.
分支節點:除了根節點和葉子節點之外的所有節點都稱為分支節點.
樹高:樹的總層數.
樹的種類
無序樹:任意子節點之間沒有順序關係,也稱自由樹
有序樹:任意節點的子節點之間有順序關係,如下:
二叉樹:如果每個節點的兒子節點不多於兩個,則稱這棵樹為二叉.每個父節點的子節點用左右兒子節點來加以區分,以左兒子節點為根的子樹稱為左子樹,以右兒子節點為根的樹稱為右子樹.
滿二叉樹:如果一個二叉樹的任何節點或者樹葉,或者恰好有兩顆非空子樹,則此二叉樹稱為滿二叉樹.
完全二叉樹:如果一棵二叉樹最多只有最下麵的兩次節點度數小於2,並且最下麵一層的節點都集中在該層的最左邊的連續位置,成稱其實完全二叉樹.
平衡二叉樹(Balanced Binary Tree)又被稱為AVL樹(有別於AVL演算法),且具有以下性質:它是一 棵空樹或它的左右兩個子樹的高度差的絕對值不超過1,並且左右兩個子樹都是一棵平衡二叉樹.
儲存:鏈式儲存。
紅黑樹: 在平衡二叉樹穩定性的基礎上,再優化一下,減少旋轉次數 特性: 1、每個節點要麼是紅色,要麼是黑色。 2、根節點必須是黑色。 3、紅色節點不能連續(也即是,紅色節點的孩子和父親都不能是紅色)。 4、對於每個節點,從該點至null(樹尾端)的任何路徑,都含有相同個數的黑色節點。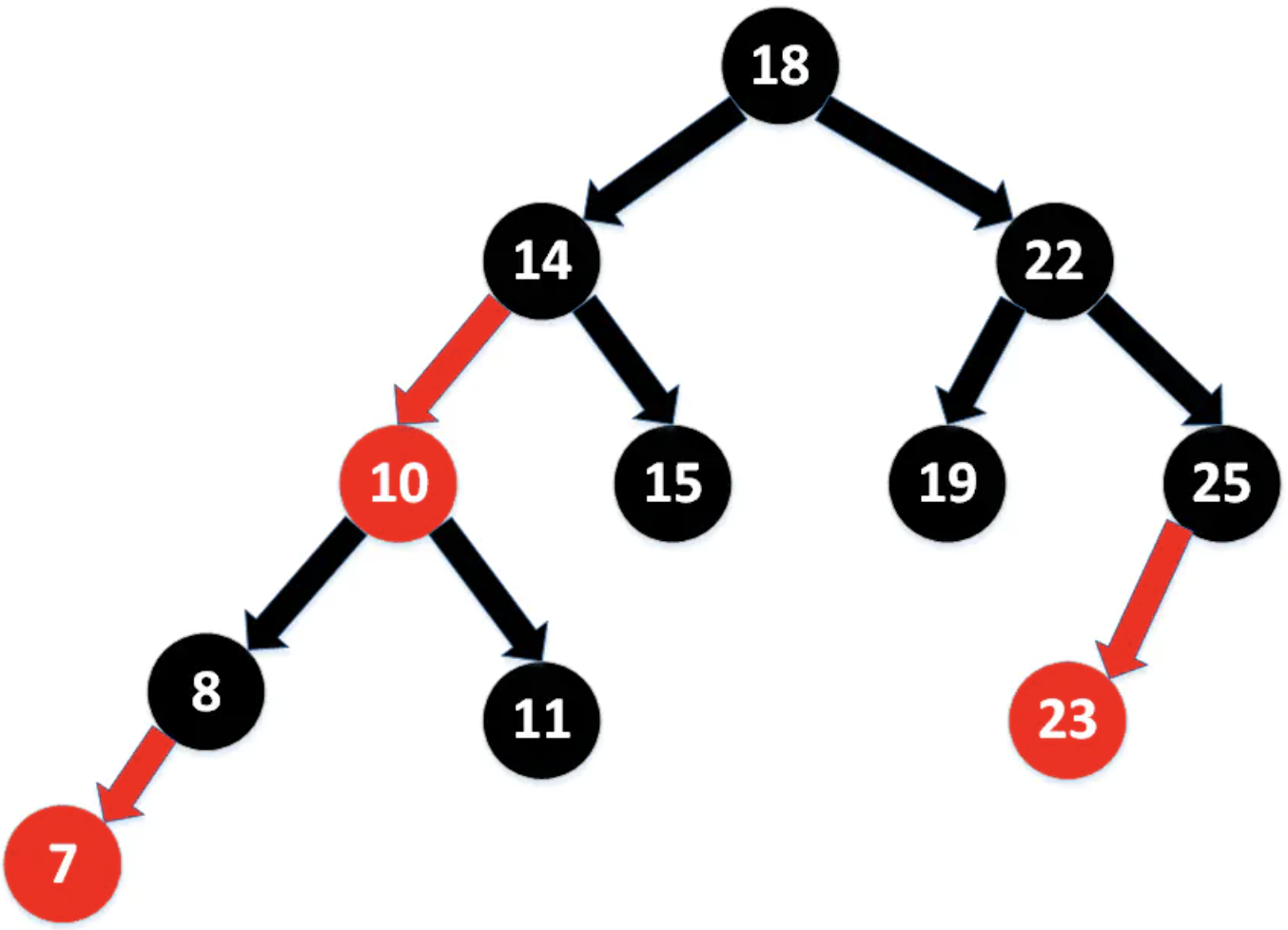
二叉樹特點:查找速度和比較次數最小,但是磁碟IO,當數據量過大的時候,索引大小可能有幾個G,不可能全都載入到記憶體
引出下麵的樹更穩
B樹與B+樹
B樹 、B - 樹都讀B樹。
B樹與B+樹區別:
B樹每個節點都存儲數據,所有節點組成這棵樹。B+樹只有葉子節點存儲數據(B+數中有兩個頭指針:一個指向根節點,另一個指向關鍵字最小的葉節點),葉子節點包含了這棵樹的所有數據,所有的葉子結點使用鏈表相連,便於區間查找和遍歷,所有非葉節點起到索引作用。
B樹中葉節點包含的關鍵字和其他節點包含的關鍵字是不重覆的,B+樹的索引項只包含對應子樹的最大關鍵字和指向該子樹的指針,不含有該關鍵字對應記錄的存儲地址。
B樹中每個節點(非根節點)關鍵字個數的範圍為[m/2(向上取整)-1,m-1](根節點為[1,m-1]),並且具有n個關鍵字的節點包含(n+1)棵子樹。B+樹中每個節點(非根節點)關鍵字個數的範圍為[m/2(向上取整),m](根節點為[1,m]),具有n個關鍵字的節點包含(n)棵子樹。
B+樹中查找,無論查找是否成功,每次都是一條從根節點到葉節點的路徑。
B樹的優點:
b+樹的中間節點不保存數據,能容納更多節點元素。
B樹的每一個節點都包含key和value,因此經常訪問的元素可能離根節點更近,因此訪問也更迅速。
M階B+數特點
有n棵子樹的非葉子結點中含有n個關鍵字(b樹是n-1個),這些關鍵字不保存數據,只用來索引,所有數據都保存在葉子節點(b樹是每個關鍵字都保存數據)。
所有的葉子結點中包含了全部關鍵字的信息,及指向含這些關鍵字記錄的指針,且葉子結點本身依關鍵字的大小自小而大順序鏈接(葉子節點組成一個鏈表)。
所有的非葉子結點可以看成是索引部分,結點中僅含其子樹中的最大(或最小)關鍵字。
通常在b+樹上有兩個頭指針,一個指向根結點,一個指向關鍵字最小的葉子結點。
同一個數字會在不同節點中重覆出現,根節點的最大元素就是b+樹的最大元素。
B樹和B+樹的共同優點
考慮磁碟IO的影響,它相對於記憶體來說是很慢的。資料庫索引是存儲在磁碟上的,當數據量大時,就不能把整個索引全部載入到記憶體了,只能逐一載入每一個磁碟頁(對應索引樹的節點)。所以我們要減少IO次數,對於樹來說,IO次數就是樹的高度,而“矮胖”就是b樹的特征之一,m的大小取決於磁碟頁的大小。
雖然查詢次數比二叉樹多,尤其當單一節點元素多時,但是相比磁碟IO速度,記憶體中的比較耗時幾乎可以忽略
所以只要樹的高度是夠低,IO次數是足夠少,就可以提升查找性能
IO:每一次讀取的數據稱之為一頁.
B樹與B+樹比較:
- 同樣大小的磁碟頁B+樹可以容納更多的節點元素,也就意味著B+樹更矮胖,查詢時IO次數更少;
- B+樹的查詢必須最終是葉子節點,而B-樹只要找到匹配元素即可,因此,B+樹查找性能穩定,B樹不穩定;
- 範圍查詢簡便,所有的葉子結點使用有序鏈表相連,便於區間查找和遍歷.
B樹示意圖: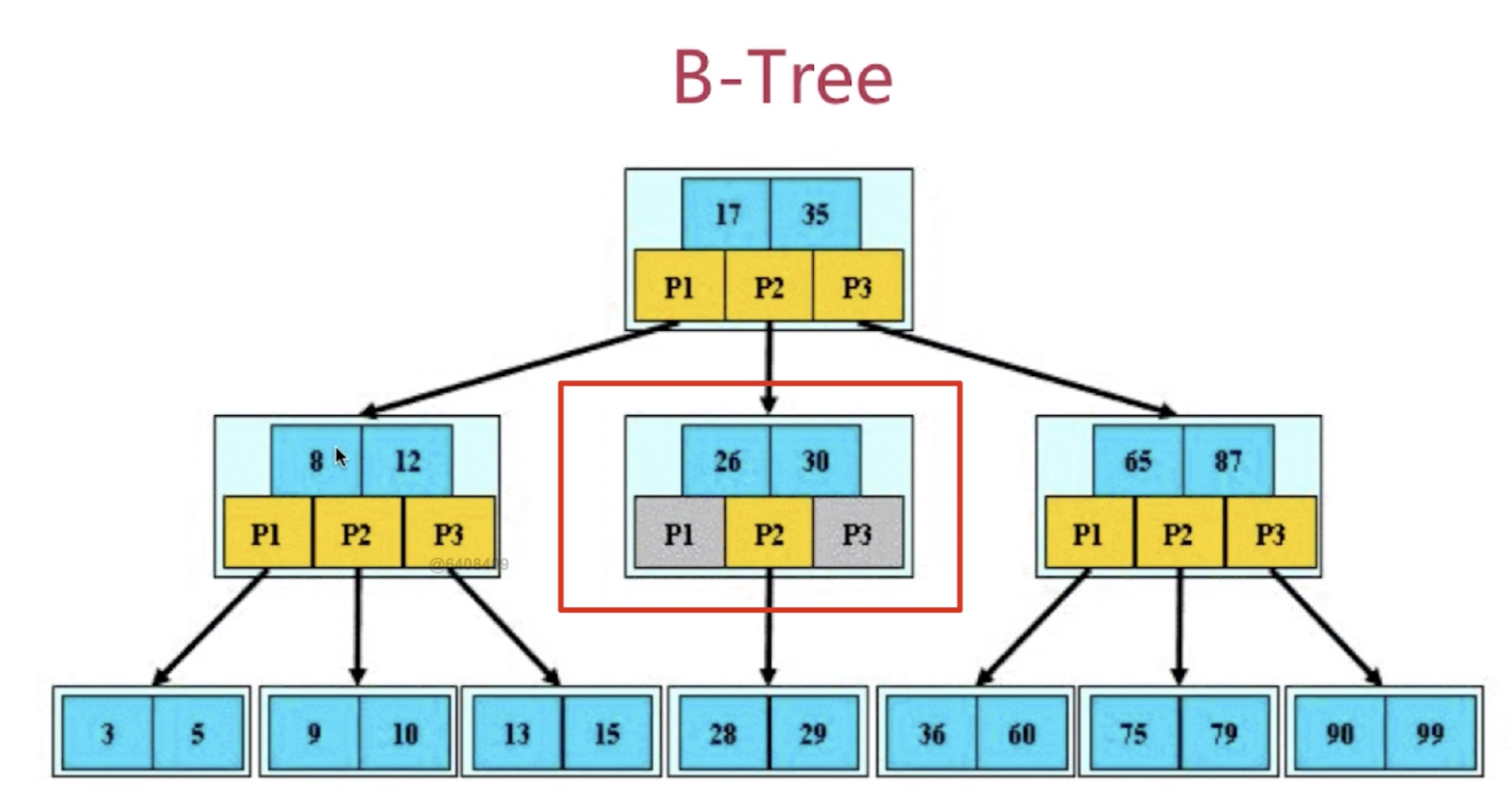
以下為 B+樹示意圖:


存儲引擎: MyISAM和InnoDB
在MySQL中,最常用的兩個存儲引擎是MyISAM和InnoDB,它們對索引的實現方式是不同的
MyISAM : data存的是數據地址。索引是索引,數據是數據。索引放在XX.MYI文件中,數據放在XX.MYD文件中,所以也叫非聚集索引
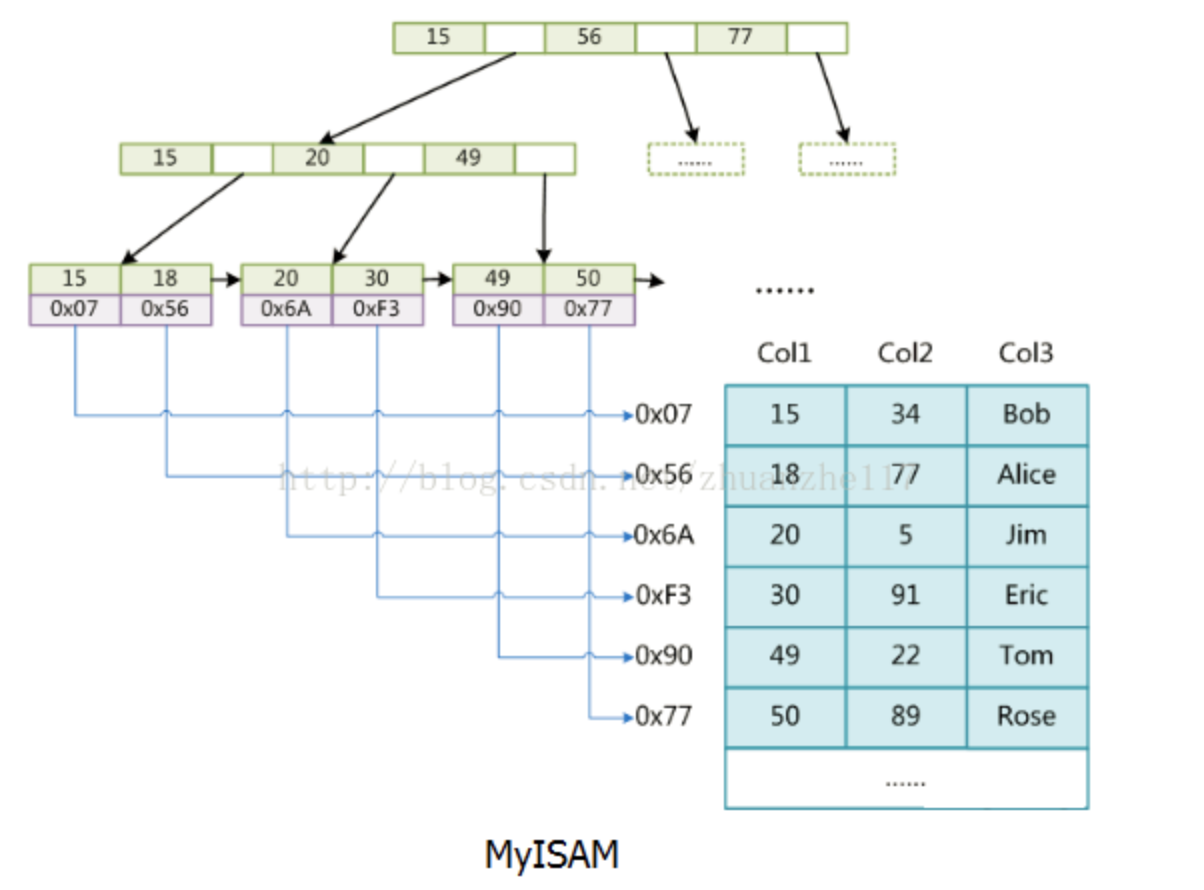
InnoDB: data存的是數據本身。索引也是數據。數據和索引存在一個XX.IDB文件中,所以也叫聚集索引。
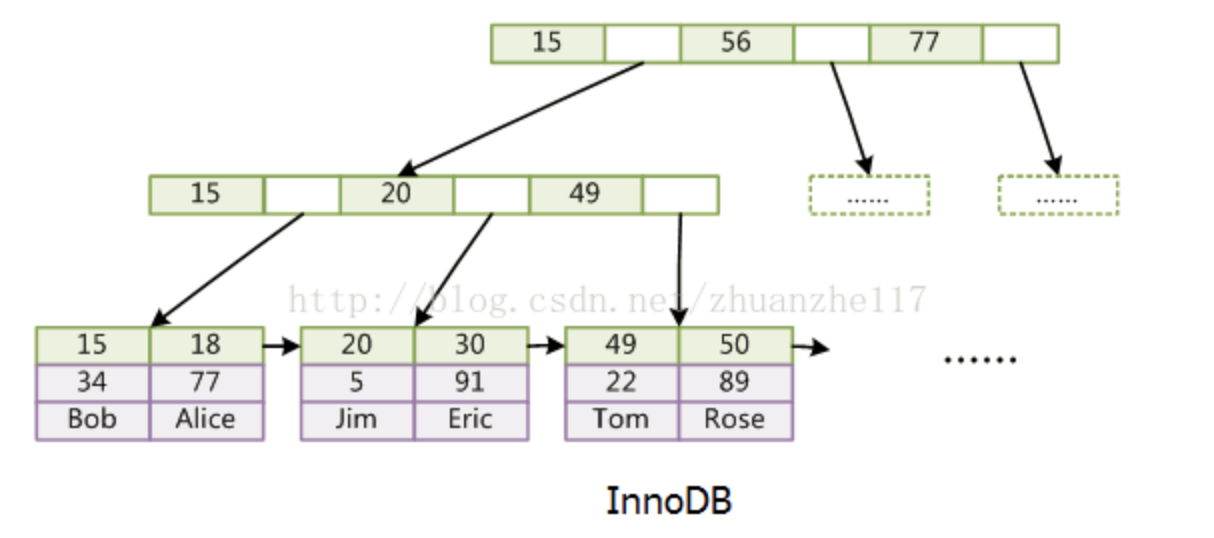
我們的Mysql資料庫用的InnoDB。
瞭解了數據結構再看索引,一切都不費解了,只是順著邏輯推而已。另加兩種存儲引擎的區別:
1、MyISAM是非事務安全的,而InnoDB是事務安全的
2、MyISAM鎖的粒度是表級的,而InnoDB支持行級鎖
3、MyISAM支持全文類型索引,而InnoDB支持全文索引
4、MyISAM相對簡單,效率上要優於InnoDB,小型應用可以考慮使用MyISAM
5、MyISAM表保存成文件形式,跨平臺使用更加方便
6、MyISAM管理非事務表,提供高速存儲和檢索以及全文搜索能力,如果在應用中執行大量select操作可選擇
7、InnoDB用於事務處理,具有ACID事務支持等特性,如果在應用中執行大量insert和update操作,可選擇。
參考文獻:
https://www.cnblogs.com/daguozb/p/8665506.html
https://www.cnblogs.com/Ash-ly/p/5459688.html
https://www.jianshu.com/p/f456d7c80ffb
https://blog.csdn.net/weixin_42228338/article/details/97684517
https://blog.csdn.net/zhuanzhe117/article/details/78039692



