基礎數據結構

来源:https://www.cnblogs.com/guokaifeng/archive/2020/05/02/12819778.html
-Advertisement-
Play Games

基礎數據結構 棧（stack） 隊列 (queue) 雙端隊列 ( deque ) 順序表 與 記憶體 簡單瞭解一下記憶體 順序表 順序表的弊端：順序表的結構需要預先知道數據大小來申請連續的存儲空間，而在進行擴充時又需要進行數據的搬遷。 鏈表 （Linked list） 二叉樹 二叉樹 根節點 葉子節點 ...


基礎數據結構

棧（stack）

  棧（stack）又名堆棧，它是一種運算受限的線性表。其限制是僅允許在表的一端進行插入和刪除運算。
這一端被稱為棧頂，相對地，把另一端稱為棧底。向一個棧插入新元素又稱作進棧、入棧或壓棧，
它是把新元素放到棧頂元素的上面，使之成為新的棧頂元素；從一個棧刪除元素又稱作出棧或退棧，
它是把棧頂元素刪除掉，使其相鄰的元素成為新的棧頂元素。

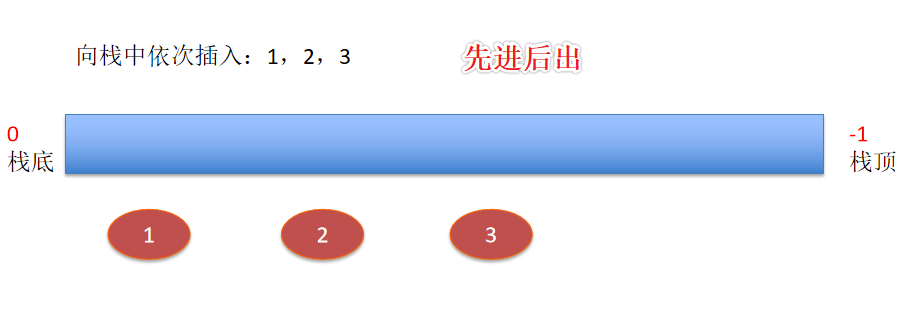
棧作為一種數據結構，是一種只能在一端進行插入和刪除操作的特殊線性表。它按照先進後出的原則存儲數據，
先進入的數據被壓入棧底，最後的數據在棧頂，需要讀數據的時候從棧頂開始彈出數據（最後一個數據被第一個讀出來）。
棧具有記憶作用，對棧的插入與刪除操作中，不需要改變棧底指針。

- 特性：先進後出的數據結構

# 應用：每個 web 瀏覽器都有一個返回按鈕。當你瀏覽網頁時，這些網頁被放置在一個棧中（實際是網頁的網址）。
你現在查看的網頁在頂部，你第一個查看的網頁在底部。如果按‘返回’按鈕，將按相反的順序瀏覽剛纔的頁面。

# 使用python代碼實現一個棧
- Stack() 創建一個空的新棧。 它不需要參數，並返回一個空棧。
- push(item)將一個新項添加到棧的頂部。它需要 item 做參數並不返回任何內容。
- pop() 從棧中刪除頂部項。它不需要參數並返回 item 。棧被修改。
- peek() 從棧返回頂部項，但不會刪除它。不需要參數。 不修改棧。
- isEmpty() 測試棧是否為空。不需要參數，並返回布爾值。
- size() 返回棧中的 item 數量。不需要參數，並返回一個整數。

class Stack():
    def __init__(self):
        self.items = []
    def push(self,item):
        self.items.append(item)
    def pop(self):
        return self.items.pop()
    def peek(self):
        return len(self.items) - 1
    def isEmpty(self):
        return self.items == []
    def size(self):
        return len(self.items)
    
stack = Stack()
stack.push(1)
stack.push(2)
stack.push(3)

print('棧頂元素下標：',stack.peek())
print(stack.isEmpty())
print('元素個數：',stack.size())
print(stack.pop())
print(stack.pop())
print(stack.pop())

隊列 (queue)

- 隊列：先進先出
- 應用場景：
    - 我們的電腦實驗室有 30 台電腦與一臺印表機聯網。當學生想要列印時，
他們的列印任務與正在等待的所有其他列印任務“一致”。第一個進入的任務是先完成。
如果你是最後一個，你必須等待你前面的所有其他任務列印。

# 使用python代碼實現一個隊列
- Queue() 創建一個空的新隊列。 它不需要參數，並返回一個空隊列。
- enqueue(item) 將新項添加到隊尾。 它需要 item 作為參數，並不返回任何內容。
- dequeue() 從隊首移除項。它不需要參數並返回 item。 隊列被修改。
- isEmpty() 查看隊列是否為空。它不需要參數，並返回布爾值。
- size() 返回隊列中的項數。它不需要參數，並返回一個整數。

class Queue():
    def __init__(self):
        self.items = []
    def enqueue(self,item):
        self.items.insert(0,item)
    def dequeue(self):
        return self.items.pop()
    def isEmpty(self):
        return self.items == []
    def size(self):
        return len(self.items)

q = Queue()
q.enqueue(1)
q.enqueue(2)
q.enqueue(3)
print(q.dequeue())
print(q.dequeue())
print(q.dequeue())    

# 面試題
- 燙手的山芋
    - 燙手山芋游戲介紹：6個孩子圍城一個圈，排列順序孩子們自己指定。第一個孩子手裡有一個燙手的山芋，
需要在計時器計時1秒後將山芋傳遞給下一個孩子，依次類推。規則是，在計時器每計時7秒時，手裡有山芋的孩子退出游戲。
該游戲直到剩下一個孩子時結束，最後剩下的孩子獲勝。請使用隊列實現該游戲策略，排在第幾個位置最終會獲勝。
# 解題思路
    - 讓手裡有山芋的孩子永遠排在隊列的頭部
class Queue():
    def __init__(self):
        self.items = []
    def enqueue(self,item):
        self.items.insert(0,item)
    def dequeue(self):
        return self.items.pop()
    def isEmpty(self):
        return self.items == []
    def size(self):
        return len(self.items)
    
kids = ['A','B','C','D','E','F']
queue = Queue()
for kid in kids:
    queue.enqueue(kid) #A對頭F隊尾
while queue.size() > 1:
    for i in range(6): #每迴圈一次，山芋傳遞一次，手裡有山芋的孩子永遠在對頭位置
        kid = queue.dequeue()
        queue.enqueue(kid)
    queue.dequeue()
print('獲勝的選手是：',queue.dequeue())
for a in range(len(kids)):
    if kids[a] == kid:   
        print('排在第：%d會獲勝'%a)  
# 執行結果
獲勝的選手是： E
排在第：4會獲勝


# 面試題 使用兩個隊列實現一個棧
class Queue():
    def __init__(self):
        self.items = []
    def enqueue(self,item):
        self.items.insert(0,item)
    def dequeue(self):
        return self.items.pop()
    def size(self):
        return len(self.items)
    
alist = [1,2,3,4,5]
q1 = Queue()
for i in alist:
    q1.enqueue(i)
q2 = Queue()
while q1.size() > 0:
    #將q1中的n-1個值取出放入到q2中
    while q1.size() > 1:
        item = q1.dequeue()
        q2.enqueue(item)
    print(q1.dequeue())

    q1,q2 = q2,q1

雙端隊列 ( deque )

同隊列相比，有兩個頭部和尾部。可以在雙端進行數據的插入和刪除，提供了單數據結構中棧和隊列的特性.

# 用python代碼實現一個雙端隊列
- Deque() 創建一個空的新 deque。它不需要參數，並返回空的 deque。
- addFront(item) 將一個新項添加到 deque 的首部。它需要 item 參數 並不返回任何內容。
- addRear(item) 將一個新項添加到 deque 的尾部。它需要 item 參數並不返回任何內容。
- removeFront() 從 deque 中刪除首項。它不需要參數並返回 item。deque 被修改。
- removeRear() 從 deque 中刪除尾項。它不需要參數並返回 item。deque 被修改。
- isEmpty() 測試 deque 是否為空。它不需要參數，並返回布爾值。
- size() 返回 deque 中的項數。它不需要參數，並返回一個整數。

class Deque():
    def __init__(self):
        self.items = []
    def addFront(self,item):
        self.items.insert(0,item)
    def addRear(self,item):
        self.items.append(item)
    def removeFront(self):
        return self.items.pop()
    def removeRear(self):
        return self.items.pop(0)
    def isEmpty(self):
        return self.items == []
    def size(self):
        return len(self.items)
    
q = Deque()
q.addFront(1)
q.addFront(2)
q.addFront(3)

print(q.removeRear())
print(q.removeRear())
print(q.removeRear())

- 雙端隊列應用案例：迴文檢查
    - 迴文是一個字元串，讀取首尾相同的字元，例如，radar toot madam。
class Deque():
    def __init__(self):
        self.items = []
    def addFront(self,item):
        self.items.insert(0,item)
    def addRear(self,item):
        self.items.append(item)
    def removeFront(self):
        return self.items.pop()
    def removeRear(self):
        return self.items.pop(0)
    def isEmpty(self):
        return self.items == []
    def size(self):
        return len(self.items)
    
def isHuiWen(s):
    ex = True
    q = Deque()
    for ch in s:
        q.addFront(ch)
    while q.size() > 1:
        if q.removeFront() != q.removeRear():
            ex = False
            break
    return ex
print(isHuiWen('上海自來水來自海上'))
# 執行結果
True

順序表 與 記憶體

  • 簡單瞭解一下記憶體

- 記憶體在電腦的作用
    - 用來存儲和運算二進位的數據
- 問題：電腦如何計算1+2？
    - 將1和2的二進位類型的數據載入到電腦的記憶體中，然後使用寄存器進行數值的預算。
- 變數的概念
    - 變數可以理解為某一塊記憶體(實際是引用的某一塊記憶體的地址)
    - 記憶體空間是有兩個預設的屬性：
        - 記憶體空間的大小
            - bit（位）：一個bit大小的記憶體空間只能存放一位二進位的數
            - byte（位元組）：8bit
            - kb：1024byte
        - 記憶體空間的地址
            - 使用一個十六進位的數值表示
            - 作用：讓cup定址
                       
- 理解a=10的記憶體圖（引用，指向）
    - 引用：變數==》記憶體空間的地址
    - a = 10：a變數/引用/記憶體空間的地址
    - 指向：如果變數或者引用表示的是某一塊記憶體空間地址的話，則該變數或者該引用指向了該塊記憶體

  • 順序表

- 集合中存儲的元素是有順序的，順序表的結構可以分為兩種形式：單數據類型(np.array數組)和多數據類型(列表,元組)。

- python中的列表和元組就屬於多數據類型的順序表

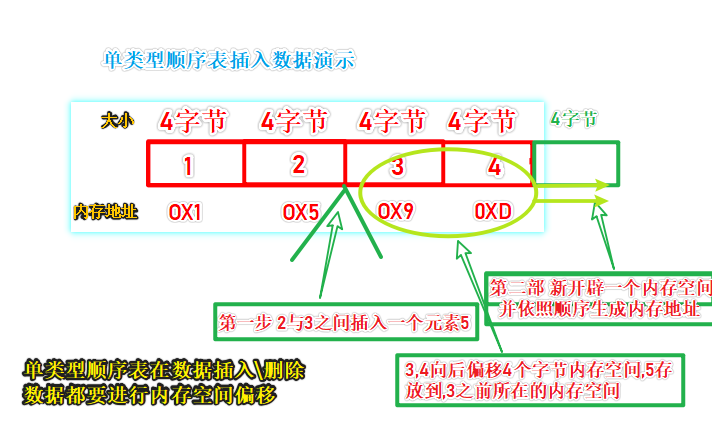
- 單數據類型順序表的記憶體圖 (記憶體連續開闢,每個記憶體空間大小一致)


- 多數據類型順序表的記憶體圖（記憶體非連續開闢）

  • 順序表的弊端：順序表的結構需要預先知道數據大小來申請連續的存儲空間，而在進行擴充時又需要進行數據的搬遷。

鏈表 （Linked list）

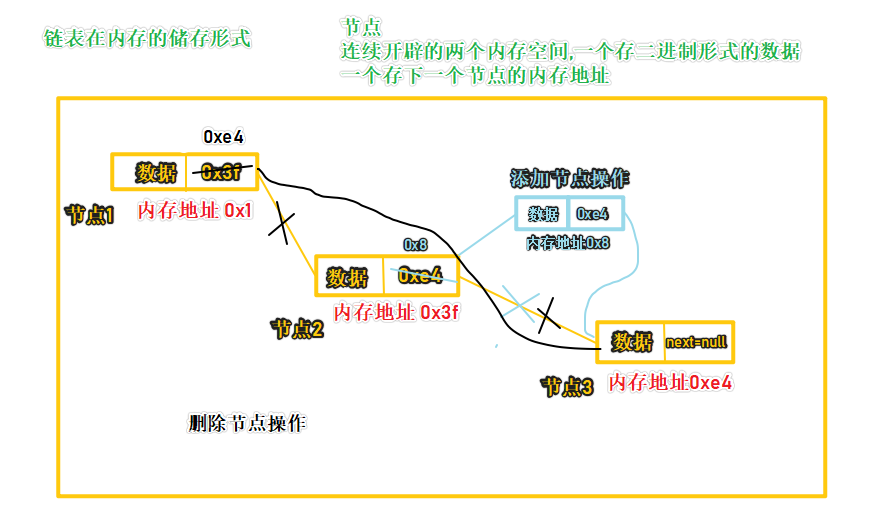
- 鏈表（Linked list）是一種常見的基礎數據結構，是一種線性表，但是不像順序表一樣連續存儲數據，
而是每一個結點（數據存儲單元）里存放下一個結點的信息（即地址）

- 相對於順序表，鏈表結構可以充分利用電腦記憶體空間，實現靈活的記憶體動態管理且進行擴充時不需要進行數據搬遷。


- 使用python實現單向鏈表

. is_empty()：鏈表是否為空

. length()：鏈表長度

. travel()：遍歷整個鏈表

. add(item)：鏈表頭部添加元素

. append(item)：鏈表尾部添加元素

. insert(pos, item)：指定位置添加元素

. remove(item)：刪除節點

. search(item)：查找節點是否存在

# 代碼
class Node():
    def __init__(self,item):
        self.item = item
        self.next = None
        
class Link():
    def __init__(self):
        #構造出一個空鏈表
        #_head存儲的只能是空或者第一個節點的地址
        self._head = None
    #向鏈表的頭部插入一個節點
    def add(self,item):
        #創建一個新的節點
        node = Node(item)
        node.next = self._head
        self._head = node
        
    def travel(self):
        #_head在鏈表創建好之後一定是不可變
        cur = self._head
        while cur:
            print(cur.item)
            cur = cur.next
            
    def isEmpty(self):
        return self._head == None
    
    def size(self):
        cur = self._head
        count = 0
        while cur:
            count += 1
            cur = cur.next
        return count
    
    def append(self,item):
        node = Node(item)
        #特殊情況
        if self._head == None:
            self._head = node
            return
        
        cur = self._head
        pre = None#pre指向的是cur前一個節點
        while cur:
            pre = cur
            cur = cur.next
        pre.next = node
    
    def search(self,item):
        find = False
        
        cur = self._head
        while cur:
            if cur.item == item:
                find = True
                break
            cur = cur.next
        
        return find
    
    def insert(self,pos,item):
        node = Node(item)
        pre = None
        cur = self._head
        for i in range(pos):
            pre = cur
            cur = cur.next
        pre.next = node
        node.next = cur
        
    def remove(self,item):
        cur = self._head
        pre = None
        #刪除的是第一個節點
        if cur.item == item:
            self._head = cur.next
            return
        while cur:  
            pre = cur
            cur = cur.next
            if cur.next == None:
                return
            if cur.item == item:
                pre.next = cur.next
                return      

- 如何實現將單鏈表倒置

# 單鏈表（插入，刪除，遍歷）
class Node():
   def __init__(self,item):
       self.item = item
       self.next = None
class Link():
   def __init__(self):
       self._head = None
   def append(self,item):
       node = Node(item)
       if self._head == None:
           self._head = node
           return
       cur = self._head
       pre = None
       
       while cur:
           pre = cur
           cur = cur.next
       pre.next = node
   def travel(self):
       cur = self._head
       while cur:
           print(cur.item)
           cur = cur.next
   def remove(self,item):
       cur = self._head
       pre = None
       #刪除的是第一個節點
       if cur.item == item:
           self._head = cur.next
           return
       while cur:
           pre = cur
           cur = cur.next
           if item == cur.item:
               pre.next = cur.next
               return
   
   def reverse(self):
       cur = self._head
       pre = None
       next_node = cur.next
       
       while cur:
           cur.next = pre
           pre = cur
           cur = next_node
           if cur:
               next_node = cur.next
       self._head = pre
   
# 雙向鏈表就是連續開闢三個記憶體空間,分別存放 數據 上個節點記憶體地址 下個節點記憶體地址

二叉樹

  • 二叉樹
    • 根節點
    • 葉子節點：
      • 左葉子節點
      • 右葉子節點
    • 樹的層級/樹的高度
  • 二叉樹的遍歷
    • 廣度優先遍歷
      • 一層一層對節點進行遍歷
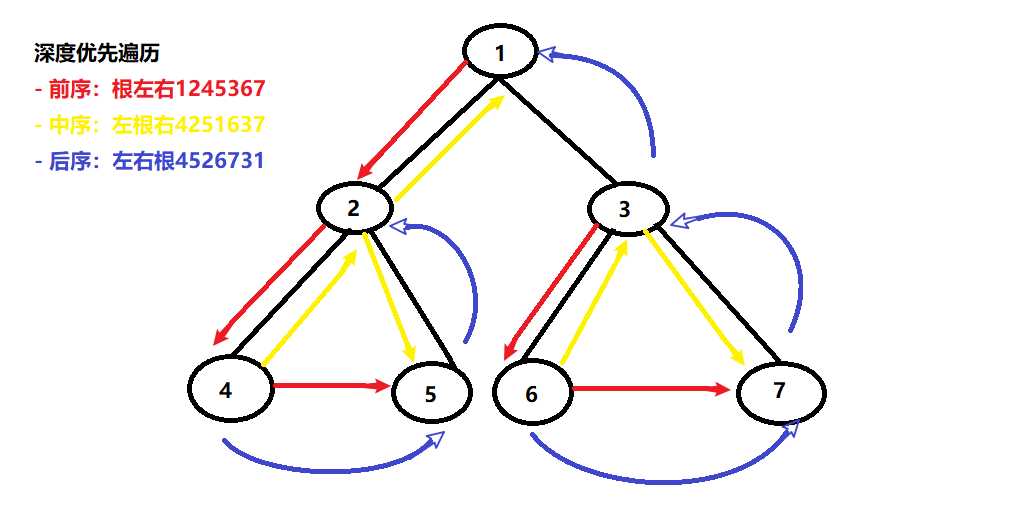
    • 深度優先遍歷
      • 前序：根左右
      • 中序：左根右
      • 後序：左右根

# 使用python代碼實現二叉樹
class Node():
    def __init__(self,item):
        self.item = item
        self.left = None
        self.right = None    
class Tree():
    def __init__(self):
        self.root = None
    def addNode(self,item):
        node = Node(item)
        #如果插入第一個節點的情況
        if self.root == None:
            self.root = node
            return
        cur = self.root
        q = [cur] #列表元素是我們進行遍歷判斷的節點
        while q:
            nd = q.pop(0)
            if nd.left == None:
                nd.left = node
                return
            else:
                q.append(nd.left)
            if nd.right == None:
                nd.right = node
                return
            else:
                q.append(nd.right)
    def travel(self):  #廣度優先遍歷
        cur = self.root
        q = [cur]
        while q:
            nd = q.pop(0)
            print(nd.item)
            if nd.left:
                q.append(nd.left)
            if nd.right:
                q.append(nd.right)
                
    def forwoar(self,root): #深度優先 前序:根左右
        if root == None:
            return
        print(root.item)
        self.forwoar(root.left)
        self.forwoar(root.right)
    def middle(self,root):  #深度優先 前序:左根右
        if root == None:
            return
        self.middle(root.left)
        print(root.item)
        self.middle(root.right)
    def back(self,root):   #深度優先 前序:左右根
        if root == None:
            return
        self.back(root.left)
        self.back(root.right)
        print(root.item)
作 者：郭楷豐 出 處：https://www.cnblogs.com/guokaifeng/ 聲援博主：如果您覺得文章對您有幫助，可以點擊文章右下角 【推薦】一下。您的鼓勵是博主的最大動力！ 自 勉：生活，需要追求；夢想，需要堅持；生命，需要珍惜；但人生的路上，更需要堅強。帶著感恩的心啟程，學會愛，愛父母，愛自己，愛朋友，愛他人。
您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • Vue使用rem做自適應佈局
    安裝插件 npm install lib-flexible --save npm install px2rem-loader --save-dev 2. 配置插件 在入口文件 main.js 中引入 lib-flexible： import 'lib-flexible' 3. 在 build/uti ...
  • 原生JavaScript手寫Ajax
    1 <script> 2 // 封裝通用的xhr對象，相容各個版本 3 function creatXHR() { 4 // 判斷瀏覽器是否將XMLHttpRequest作為本地對象實現，針對IE7,firefox, opera等 5 if (typeof XMLHttpRequest != "un ...
  • 手把手教你女朋友創建一個Springboot外置Tomcat項目
    女朋友：啥SpringBoot都內置Tomcat了，為啥還要內置Tomcat？ 大佬：別跟我說什麼內置Tomcat，存在即合理，人家JetBrains公司都傻嗎，非要給Idea添加外置Tomcat的功能。 氣死我了~~~，上教程~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~·我是瑟瑟 ...
  • 從無到有，手把手教你用Maven怒草一個SpringBoot項目出來
    1、使用Navicat 新建一個資料庫 2、新建一個數據表 CREATE TABLE t_user( id int(6) PRIMARY KEY auto_increment, name VARCHAR(40), age int(3), bir TIMESTAMP ) 3、新建一個project，f ...
  • PHP 配置指令 include_path 詳解
    php.ini中有個指令，include_path 包含路徑，指定一系列路徑列表，用於下麵函數尋找文件，如 require,include,fopen(),file(),readfile() and file_get_contents(). 格式類似於系統環境變數， ，Unix用冒號(colon)分 ...
  • LeetCode 面試題15. 二進位中1的個數
    我的LeetCode：https://leetcode cn.com/u/ituring/ 我的LeetCode刷題源碼[GitHub]：https://github.com/izhoujie/Algorithmcii LeetCode 面試題15. 二進位中1的個數 與以下題目相同 前往：Leet ...
  • LeetCode 191. 位1的個數
    我的LeetCode：https://leetcode cn.com/u/ituring/ 我的LeetCode刷題源碼[GitHub]：https://github.com/izhoujie/Algorithmcii LeetCode 191. 位1的個數 題目 編寫一個函數，輸入是一個無符號整數 ...
  • pyqt5，pycharm，Process finished with exit code -1073741819 (0xC0000005)
    QMovie,多線程,pyqt5,python3 網路上找遍了，根本不是我遇到的問題啊QAQ，之後就終止了這個項目，改做其他的了 但是之後貌似發現了一點問題的思路，供大家參考： 當一個視窗被打開多次時，就會觸發這種錯誤 當多個線程擠在一起的時候，比較常見 特別是當多線程和QMovie這個東西並行的時 ...
一周排行
    -Advertisement-
    Play Games
  • 移動開發（一）：使用.NET MAUI開發第一個安卓APP
    移動開發（一）：使用.NET MAUI開發第一個安卓APP 對於工作多年的C#程式員來說，近來想嘗試開發一款安卓APP，考慮了很久最終選擇使用.NET MAUI這個微軟官方的框架來嘗試體驗開發安卓APP，畢竟是使用Visual Studio開發工具，使用起來也比較的順手，結合微軟官方的教程進行了安卓 ...
  • wpf ToggleButton選中效果和一個登錄界面
    前言 QuestPDF 是一個開源 .NET 庫，用於生成 PDF 文檔。使用了C# Fluent API方式可簡化開發、減少錯誤並提高工作效率。利用它可以輕鬆生成 PDF 報告、發票、導出文件等。 項目介紹 QuestPDF 是一個革命性的開源 .NET 庫，它徹底改變了我們生成 PDF 文檔的方 ...
  • 彈幕樹洞項目功能新增篇
    項目地址 項目後端地址： https://github.com/ZyPLJ/ZYTteeHole 項目前端頁面地址： ZyPLJ/TreeHoleVue (github.com) https://github.com/ZyPLJ/TreeHoleVue 目前項目測試訪問地址： http://tree ...
  • 第27篇 sqlserver2022詳細安裝步驟
    話不多說，直接開乾 一.下載 1.官方鏈接下載： https://www.microsoft.com/zh-cn/sql-server/sql-server-downloads 2.在下載目錄中找到下麵這個小的安裝包 SQL2022-SSEI-Dev.exe，運行開始下載SQL server； 二. ...
  • .NET 開源高性能 MQTT 類庫
    前言 隨著物聯網（IoT）技術的迅猛發展，MQTT（消息隊列遙測傳輸）協議憑藉其輕量級和高效性，已成為眾多物聯網應用的首選通信標準。 MQTTnet 作為一個高性能的 .NET 開源庫，為 .NET 平臺上的 MQTT 客戶端與伺服器開發提供了強大的支持。 本文將全面介紹 MQTTnet 的核心功能 ...
  • Serilog文檔翻譯系列（六） - 可用的接收器、增強器、格式化輸出
    Serilog支持多種接收器用於日誌存儲，增強器用於添加屬性，LogContext管理動態屬性，支持多種輸出格式包括純文本、JSON及ExpressionTemplate。還提供了自定義格式化選項，適用於不同需求。 ...
  • 警惕 Visual Studio 屬性求值副作用導致邏輯不符合預期
    目錄簡介獲取 HTML 文檔解析 HTML 文檔測試參考文章 簡介 動態內容網站使用 JavaScript 腳本動態檢索和渲染數據，爬取信息時需要模擬瀏覽器行為，否則獲取到的源碼基本是空的。 本文使用的爬取步驟如下： 使用 Selenium 獲取渲染後的 HTML 文檔 使用 HtmlAgility ...
  • [使用目前最新版]HybridCLR6.9.0+YooAsset2.2.4實現純C# Unity熱更新方案 (一)
    1.前言 什麼是熱更新 游戲或者軟體更新時，無需重新下載客戶端進行安裝，而是在應用程式啟動的情況下，在內部進行資源或者代碼更新 Unity目前常用熱更新解決方案 HybridCLR，Xlua，ILRuntime等 Unity目前常用資源管理解決方案 AssetBundles，Addressable， ...
  • 在 ASP.NET Core Web API 中使用操作篩選器統一處理通用操作
    本文章主要是在C# ASP.NET Core Web API框架實現向手機發送驗證碼簡訊功能。這裡我選擇是一個互億無線簡訊驗證碼平臺，其實像阿裡雲，騰訊雲上面也可以。 首先我們先去 互億無線 https://www.ihuyi.com/api/sms.html 去註冊一個賬號 註冊完成賬號後，它會送 ...
  • 第28篇 如何.net中實現高效可靠數據同步api
    通過以下方式可以高效，並保證數據同步的可靠性 1.API設計 使用RESTful設計，確保API端點明確，並使用適當的HTTP方法（如POST用於創建，PUT用於更新）。 設計清晰的請求和響應模型，以確保客戶端能夠理解預期格式。 2.數據驗證 在伺服器端進行嚴格的數據驗證，確保接收到的數據符合預期格 ...
所有分類