LeetCode 36. 有效的數獨

来源:https://www.cnblogs.com/izhoujie/archive/2020/04/03/12629853.html
-Advertisement-
Play Games

我的LeetCode：https://leetcode cn.com/u/ituring/ 我的LeetCode刷題源碼[GitHub]：https://github.com/izhoujie/Algorithmcii LeetCode 36. 有效的數獨 題目 判斷一個 9x9 的數獨是否有效。只 ...


我的LeetCode：https://leetcode-cn.com/u/ituring/

我的LeetCode刷題源碼[GitHub]：https://github.com/izhoujie/Algorithmcii

LeetCode 36. 有效的數獨

題目

判斷一個 9x9 的數獨是否有效。只需要__根據以下規則__，驗證已經填入的數字是否有效即可。

  1. 數字 1-9 在每一行只能出現一次。
  2. 數字 1-9 在每一列只能出現一次。
  3. 數字 1-9 在每一個以粗實線分隔的 3x3 宮內只能出現一次。

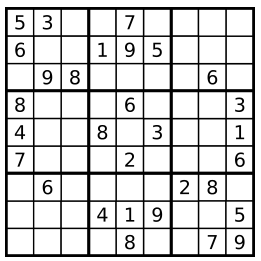
上圖是一個部分填充的有效的數獨。

數獨部分空格內已填入了數字，空白格用 '.' 表示。

示例 1:

輸入:
[
  ["5","3",".",".","7",".",".",".","."],
  ["6",".",".","1","9","5",".",".","."],
  [".","9","8",".",".",".",".","6","."],
  ["8",".",".",".","6",".",".",".","3"],
  ["4",".",".","8",".","3",".",".","1"],
  ["7",".",".",".","2",".",".",".","6"],
  [".","6",".",".",".",".","2","8","."],
  [".",".",".","4","1","9",".",".","5"],
  [".",".",".",".","8",".",".","7","9"]
]
輸出: true

示例 2:

輸入:
[
  ["8","3",".",".","7",".",".",".","."],
  ["6",".",".","1","9","5",".",".","."],
  [".","9","8",".",".",".",".","6","."],
  ["8",".",".",".","6",".",".",".","3"],
  ["4",".",".","8",".","3",".",".","1"],
  ["7",".",".",".","2",".",".",".","6"],
  [".","6",".",".",".",".","2","8","."],
  [".",".",".","4","1","9",".",".","5"],
  [".",".",".",".","8",".",".","7","9"]
]
輸出: false
解釋: 除了第一行的第一個數字從 5 改為 8 以外，空格內其他數字均與 示例1 相同。
     但由於位於左上角的 3x3 宮內有兩個 8 存在, 因此這個數獨是無效的。

說明:

  • 一個有效的數獨（部分已被填充）不一定是可解的。
  • 只需要根據以上規則，驗證已經填入的數字是否有效即可。
  • 給定數獨序列只包含數字 1-9 和字元 '.' 。
  • 給定數獨永遠是 9x9 形式的。

來源：力扣（LeetCode）
鏈接：https://leetcode-cn.com/problems/valid-sudoku
著作權歸領扣網路所有。商業轉載請聯繫官方授權，非商業轉載請註明出處。

解題思路

這道題做出來是比較簡單的，暴力來每行每豎每小宮格分別校驗就可以了，這樣看至少需要三次全掃描；
如何做到只掃描一遍就能完成呢？分析後可能發現比較難解決是小宮格的索引問題，其次如果要保存原始數據，應該需要
橫豎小宮格共三個二維數組（或者set集合），但是我們只需要知道1-9這幾個數字有還是沒有以及只能有一個，對應到編碼就是0和1，因此可以進一步壓縮二維數組為一位數組，
每個數組的int的前9個bit位用來存儲1-9是否出現過且僅出現過一次，綜上，從需要三次掃描三個二維數組到一次掃描三個二維數組再到最後一次掃描三個一維數組，演算法的效率提升是非常明顯的；

思路1-三遍掃描，橫豎小宮格各自作校驗

步驟：

  1. 新建三個set對應橫豎小宮格；
  2. 三次掃描分別校驗橫豎小宮格；

思路2-只掃描一次

只掃描一次的關鍵是定位小宮格的索引：
關鍵點小宮格的索引公式：（i/3）*3 + j/3;

可以這麼理解：
- i/3表示第幾行的小宮格，取值為0、1、2對應實際的第一、二、三行；
- （i/3）3表示第i/3的小宮格下標的的起始數字，比如第一行是從0開始，第二行是從3開始，第三行是從6開始；
- j/3表示所在行的第j/3個宮格，取值為0、1、2對應實際的第一、二、三個小宮格；
- （i/3）3 + j/3 組合起來就是：前半段表示小宮格的所在行及起始下標，後半段表示當前行的第幾個小宮格，組合的所有可能值0、1、2、3、、4、5、6、7、8就對應九個小宮格；

思路3-只掃描一次，進一步壓縮輔助空間，使用bit位記錄數據

實際做法和代碼與思路2無太大區別，唯一的區別是數組換位一維的，校驗時使用位記錄和對比校驗；

演算法源碼示例

package leetcode;

import java.util.HashSet;

/**
 * @author ZhouJie
 * @date 2020年2月1日 下午4:30:05 
 * @Description: 36. 有效的數獨
 *
 */
public class LeetCode_0036 {

}

class Solution_0036 {
	/**
	 * @author ZhouJie
	 * @date 2020年2月1日 下午8:27:14 
	 * @Description: TODO(方法簡述) 
	 * @return boolean 
	 * @UpdateUser-UpdateDate:[ZhouJie]-[2020年2月1日 下午8:27:14]  
	 * @UpdateRemark:1-行列小宮格分別遍歷校驗，使用一個set
	 *
	 */
	public boolean isValidSudoku_1(char[][] board) {
		if (board == null) {
			return false;
		}
		HashSet<Character> set = new HashSet<Character>();
		// 行列判斷
		for (int x = 0; x < 9; x++) {
			set.clear();
			// 行判斷
			for (int y = 0; y < 9; y++) {
				if (!check(set, board[x][y])) {
					return false;
				}
			}
			set.clear();
			// 列判斷
			for (int y = 0; y < 9; y++) {
				if (!check(set, board[y][x])) {
					return false;
				}
			}
		}
		// 小宮格判斷，先定位單個小宮格位置，再遍歷小宮格的數字
		for (int i = 0; i < 9; i += 3) {
			for (int j = 0; j < 9; j += 3) {
				set.clear();
				for (int x = 0; x < 3; x++) {
					for (int y = 0; y < 3; y++) {
						if (!check(set, board[x + i][y + j])) {
							return false;
						}
					}
				}
			}
		}
		return true;
	}

	private boolean check(HashSet<Character> set, char c) {
		if (c == '.') {
			return true;
		} else if (set.contains(c)) {
			return false;
		} else {
			set.add(c);
			return true;
		}
	}

	/**
	 * @author ZhouJie
	 * @date 2020年2月1日 下午8:27:38 
	 * @Description: TODO(方法簡述) 
	 * @return boolean 
	 * @UpdateUser-UpdateDate:[ZhouJie]-[2020年2月1日 下午8:27:38]  
	 * @UpdateRemark:2-行列小宮格各自使用自己的校驗空間同時校驗，一次遍歷 
	 *
	 */
	public boolean isValidSudoku_2(char[][] board) {
		// 行列小宮格的編號
		int[][] rows = new int[9][9];
		int[][] columns = new int[9][9];
		int[][] boxes = new int[9][9];

		for (int i = 0; i < 9; i++) {
			for (int j = 0; j < 9; j++) {
				char c = board[i][j];
				if (c != '.') {
					int num = c - '1';
					// 關註點，計算小宮格索引公式
					int boxIndex = (i / 3) * 3 + j / 3;
					// 行判斷
					if (rows[i][num] == 1) {
						return false;
					} else {
						rows[i][num] = 1;
					}
					// 列判斷
					if (columns[j][num] == 1) {
						return false;
					} else {
						columns[j][num] = 1;
					}
					// 小宮格判斷
					if (boxes[boxIndex][num] == 1) {
						return false;
					} else {
						boxes[boxIndex][num] = 1;
					}
				}
			}
		}
		return true;
	}

	/**
	 * @author: ZhouJie
	 * @date: 2020年4月3日 下午9:30:03 
	 * @param: @param board
	 * @param: @return
	 * @return: boolean
	 * @Description: 3-進一步壓縮空間，使bit位來計算數據
	 *
	 */
	public boolean isValidSudoku_3(char[][] board) {
		// 行列小宮格的編號
		int[] rows = new int[9];
		int[] columns = new int[9];
		int[] boxes = new int[9];

		for (int i = 0; i < 9; i++) {
			for (int j = 0; j < 9; j++) {
				char c = board[i][j];
				if (c != '.') {
					int num = c - '1';
					// 關註點，計算小宮格索引公式
					int boxIndex = (i / 3) * 3 + j / 3;
					// 行判斷
					if (((rows[i] >> num) & 1) == 1) {
						return false;
					} else {
						rows[i] |= 1 << num;
					}
					// 列判斷
					if (((columns[j] >> num) & 1) == 1) {
						return false;
					} else {
						columns[j] |= 1 << num;
					}
					// 小宮格判斷
					if (((boxes[boxIndex] >> num) & 1) == 1) {
						return false;
					} else {
						boxes[boxIndex] |= 1 << num;
					}
				}
			}
		}
		return true;
	}
}

您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • 記錄一個不同的流媒體網站實現方法，和用Python爬蟲爬它的坑
    今天找到一片電影，想把它下載下來。 先開Networks工具分析一下： 初步分析發現，視頻載入時會拉取TS格式的文件，推測這是一個m3u8的索引，記錄著幾百段TS文件，這樣方便快進時載入。 但是實際分析m3u8文件時，發現這並不是一個有效的索引文件，應該只是載入一個形式，實際的handler在其他地 ...
  • 實際開發中 dao、entity的代碼怎樣自動生成？一款工具送給你
    01 關註"一猿小講"朋友，都知道以往的文章一直倡導拒絕 CRUD，那到底什麼是 CRUD？今天咱們就聊聊 Java 妹子小猿與資料庫老頭交互的事兒。 產品小汪鏗鏘有力的說：小猿同學，咱們近期要推一爆款產品，你先實現用戶基本的登錄的功能。 啥玩意？小猿內心嘀咕嘀咕：爆款產品，還基本的登錄，那不就是實 ...
  • 徒手打造一款為業務賦能的小工具，另附實戰經驗。
    線上應用程式升級，需要把缺失的數據關聯補充一下，你寫個程式處理一下？ 客戶信息同步，由於是線上敏感欄位都是加密處理，所以需要你再寫個程式解密處理一下？ 曾記得 N 年前，我經常幹這種事情，碼這種代碼。今天回過頭來，對此類事情簡單做一個分享，以防你們也遇到此類問題，不妨拿去實踐一下，說不定會提高效率呢 ...
  • LeetCode 42. 接雨水
    我的LeetCode：https://leetcode cn.com/u/ituring/ 我的LeetCode刷題源碼[GitHub]：https://github.com/izhoujie/Algorithmcii LeetCode 42. 接雨水 題目 給定 n 個非負整數表示每個寬度為 1 ...
  • Java概述(B1)
    Java概述 Java是什麼？ Java is a general purpose programming language that is class based, object oriented, and designed to have as few implementation depend ...
  • python基礎學習-字元串常見操作
    字元串常見操作 索引 切片 字元串的常見操作 應用 判斷是否是小數 ...
  • 吐槽，Java 設計的槽點
    今天不灌水，直接上乾貨！希望下麵的講解，能與你產生一些共鳴。 1. 求長度各有千秋 你是否曾經在面試的時候，經常被問到：數組有沒有 length() 方法？字元串有沒有 length() 方法？ 集合有沒有 length() 方法？ 面對這個問題，那麼不得不吐槽一下，Java 中獲取長度的方式，設計 ...
  • java 基本數據類型對象包裝類
    byte Byte short Short int Integer long Long boolean Boolean char Character float Float double Double 基本數據類型對象包裝類最常見作用：用於基本數據類型和字元串類型之間做轉換。 基本數據類型轉成字元串 ...
一周排行
    -Advertisement-
    Play Games
  • 如何基於surging跨網關跨語言進行緩存降級
    基於.NET Framework 4.8 開發的深度學習模型部署測試平臺，提供了YOLO框架的主流系列模型，包括YOLOv8~v9，以及其系列下的Det、Seg、Pose、Obb、Cls等應用場景，同時支持圖像與視頻檢測。模型部署引擎使用的是OpenVINO™、TensorRT、ONNX runti... ...
  • 十年沉澱，重啟開發之路
    十年沉澱，重啟開發之路 十年前，我沉浸在開發的海洋中，每日與代碼為伍，與演算法共舞。那時的我，滿懷激情，對技術的追求近乎狂熱。然而，隨著歲月的流逝，生活的忙碌逐漸占據了我的大部分時間，讓我無暇顧及技術的沉澱與積累。 十年間，我經歷了職業生涯的起伏和變遷。從初出茅廬的菜鳥到逐漸嶄露頭角的開發者，我見證了 ...
  • C#.NET體系圖文概述—2024最全總結
    C# 是一種簡單、現代、面向對象和類型安全的編程語言。.NET 是由 Microsoft 創建的開發平臺，平臺包含了語言規範、工具、運行，支持開發各種應用，如Web、移動、桌面等。.NET框架有多個實現，如.NET Framework、.NET Core（及後續的.NET 5+版本），以及社區版本M... ...
  • 班級擂臺（光榮）榜 - 極簡教育小工具
    前言 本文介紹瞭如何使用三菱提供的MX Component插件實現對三菱PLC軟元件數據的讀寫，記錄了使用電腦模擬，模擬PLC，直至完成測試的詳細流程，並重點介紹了在這個過程中的易錯點，供參考。 用到的軟體： 1. PLC開發編程環境GX Works2，GX Works2下載鏈接 https:// ...
  • web server apache tomcat11-31-websocket
    前言 整理這個官方翻譯的系列，原因是網上大部分的 tomcat 版本比較舊，此版本為 v11 最新的版本。 開源項目 從零手寫實現 tomcat minicat 別稱【嗅虎】心有猛虎，輕嗅薔薇。 系列文章 web server apache tomcat11-01-官方文檔入門介紹 web serv ...
  • day31-jQuery
    1、jQuery介紹 jQuery是什麼 jQuery是一個快速、簡潔的JavaScript框架，是繼Prototype之後又一個優秀的JavaScript代碼庫（或JavaScript框架）。jQuery設計的宗旨是“write Less，Do More”，即倡導寫更少的代碼，做更多的事情。它封裝 ...
  • aardio爬蟲) 實戰篇：逆向有道翻譯web介面
    前言 之前的文章把js引擎(aardio封裝庫) 微軟開源的js引擎(ChakraCore))寫好了，這篇文章整點js代碼來測一下bug。測試網站：https://fanyi.youdao.com/index.html#/ 逆向思路 逆向思路可以看有道翻譯js逆向（MD5加密，AES加密）附完整源碼 ...
  • 面試官：這就是你理解的Java多線程基礎？
    引言 現代的操作系統（Windows，Linux，Mac OS）等都可以同時打開多個軟體（任務），這些軟體在我們的感知上是同時運行的，例如我們可以一邊瀏覽網頁，一邊聽音樂。而CPU執行代碼同一時間只能執行一條，但即使我們的電腦是單核CPU也可以同時運行多個任務，如下圖所示，這是因為我們的 CPU 的 ...
  • Python文本統計與分析從基礎到進階
    掌握使用Python進行文本英文統計的基本方法，並瞭解如何進一步優化和擴展這些方法，以應對更複雜的文本分析任務。 ...
  • Redis多數據源，看這篇就夠了
    背景 Redis多數據源常見的場景： 分區數據處理：當數據量增長時，單個Redis實例可能無法處理所有的數據。通過使用多個Redis數據源，可以將數據分區存儲在不同的實例中，使得數據處理更加高效。 多租戶應用程式：對於多租戶應用程式，每個租戶可以擁有自己的Redis數據源，以確保數據隔離和安全性。 ...
所有分類