我的LeetCode：https://leetcode-cn.com/u/ituring/

我的LeetCode刷題源碼[GitHub]：https://github.com/izhoujie/Algorithmcii

LeetCode 42. 接雨水

題目

給定 n 個非負整數表示每個寬度為 1 的柱子的高度圖，計算按此排列的柱子，下雨之後能接多少雨水。

上面是由數組 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度圖，在這種情況下，可以接 6 個單位的雨水（藍色部分表示雨水）。 感謝 Marcos 貢獻此圖。

示例:

輸入: [0,1,0,2,1,0,1,3,2,1,2,1]
輸出: 6

來源：力扣（LeetCode）
鏈接：https://leetcode-cn.com/problems/trapping-rain-water
著作權歸領扣網路所有。商業轉載請聯繫官方授權，非商業轉載請註明出處。

解題思路

只要記住水往低處流，所以我們只要關註較低的柱子就行；
想象數組左右兩側都有一個限高柱，然後左右指針分別依次往裡推進，每次左右中較低的柱子用來跟於它同側的限高柱比較，若低於限高柱表示可搜集，否則更新該側限高柱，同時該側指針內移，進入下個迴圈；
另一個思路是直接計算面積差，詳細看圖解；

思路1-滑動視窗思想

把數組整個看做一個滑動視窗，左右邊界有限高柱，左右指針交替內移；

1. 初始化左右邊界限高柱為左右邊界值；
2. 左右指針交替往內搜集雨水：每次較小的指針跟與其同側的限高柱對比，小於說明可搜集差值的雨水，否則更新該側的限高柱為當前指針值，然後指針內移；
3. 重覆2邏輯直至左右指針相遇；

總結：滑動視窗/動態規劃的核心是找到狀態量的轉移，或者說是轉移方程，本題若f(n)表示數組值，對於左側限高柱的邏輯則 f(n)=max(f(n),f(n+1))，同時可搜集的雨水為f(n)>f(n+1)?f(n)-f(n+1):0；

思路1-面積差數學直接求解

面積差計算步驟：

1. 從左往右掃描一遍，逐次求最大值累加；
2. 從右向左掃描一遍，逐次求最大值累加和；
3. 減去原來數組的面積和步驟1、2中最大值與數組長度構成的矩形的面積；
   直接看會懵的，看圖解配代碼就明白了:
   

核心代碼：
代碼很簡單，耐心先看明白代碼做了什麼，然後看圖解；

while (i < len) {
	// 從左向右不斷求最大值，向右平鋪面積值
	leftMax = Math.max(leftMax, height[i]);
	// 從右向左不斷求最大值，向左平鋪面積值
	rightMax = Math.max(rightMax, height[j - i]);
	// 順帶減去原數組的面積值
	rst += leftMax + rightMax - height[i++];
}
// 最後減去平鋪後最高點與數組長度組成的矩形面積就是雨水面積
return rst - len * leftMax;

代碼分解看：

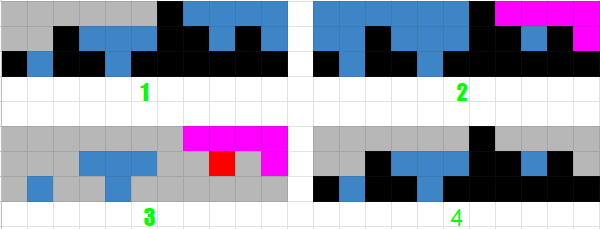
• 先看leftMax = Math.max(leftMax, height[i]);和rst+=leftMax 部分，這裡最後累加的就是圖1的面積（所有顏色）；
• 再看rightMax = Math.max(rightMax, height[j - i]);和rst+=rightMax 部分，這裡最後累加的就是圖2的面積（不包括粉色部分）；
• 然後看一下rst+=leftMax - height[i++]部分，這裡最後得到的是圖3表示的面積（所有顏色）；
• 重點是，我們得到的圖3中，如果取出粉色部分加到圖2上就會得到一個最大值與數組長度組成的完整矩形，並且圖3中紅色的部分在圖2中重覆計算了一次，
  所以實際上rst += leftMax + rightMax - height[i++];這裡我們最後拿到的雨水的面積加整個矩形的面積再加紅色部分的面積，那麼，如果我們減去矩形部分的面積（紅色部分只減去了一次）不就得到雨水的面積了麽？Bingo!!!
• 所以最後return rst - len * leftMax; 代碼這裡我們再減去矩形的面積就可以了，即最終圖4中淡藍色部分的雨水面積；

演算法源碼示例

package leetcode;

/**
 * @author ZhouJie
 * @date 2020年2月1日 下午10:44:25 
 * @Description: 42. 接雨水
 *
 */
public class LeetCode_0042 {

}

class Solution_0042 {
	/**
	 * @author ZhouJie
	 * @date 2020年2月1日 下午11:52:28 
	 * @Description: TODO(方法簡述) 
	 * @return int 
	 * @UpdateUser-UpdateDate:[ZhouJie]-[2020年2月1日 下午11:52:28]  
	 * @UpdateRemark:1- 
	 *
	 */
	public int trap_1(int[] height) {
		if (height == null) {
			return 0;
		}
		int rst = 0, leftMax = 0, rightMax = 0;
		int i = 0, j = height.length - 1;
		while (i < j) {
			// 若左側擋板低，則由左側向內搜集雨水，否則從右側向內搜集
			if (height[i] < height[j]) {
				if (height[i] < leftMax) {
					rst += leftMax - height[i];
				} else {
					leftMax = height[i];
				}
				i++;
			} else {
				if (height[j] < rightMax) {
					rst += rightMax - height[j];
				} else {
					rightMax = height[j];
				}
				j--;
			}
		}
		return rst;
	}

	/**
	 * @author: ZhouJie
	 * @date: 2020年4月4日 上午2:03:37 
	 * @param: @param height
	 * @param: @return
	 * @return: int
	 * @Description: 2-面積差法，數學方法；
	 *
	 */
	public int trap_2(int[] height) {
		if (height == null) {
			return 0;
		}
		int rst = 0, leftMax = 0, rightMax = 0, len = height.length;
		int i = 0, j = len - 1;
		while (i < len) {
			// 從左向右不斷求最大值，向右平鋪面積值
			leftMax = Math.max(leftMax, height[i]);
			// 從右向左不斷求最大值，向左平鋪面積值
			rightMax = Math.max(rightMax, height[j - i]);
			// 順帶減去原數組的面積值
			rst += leftMax + rightMax - height[i++];
		}
		// 最後減去平鋪後最高點與數組長度組成的矩形面積就是雨水面積
		return rst - len * leftMax;
	}
}