樹的基本概念和常用術語 節點的度:一個結點的兒子結點個數稱為該節點的度 樹的度:一棵樹的度是指該樹中結點的最大度數。如上圖的樹的度是3 葉節點或終端節點:度為零的節點。如上圖中E,I,J,C,G,H是葉節點 非終端節點或分支節點:度不為零的節點。除根節點外的分支節點都叫做內部節點。 路徑:若存在樹中 ...
樹的基本概念和常用術語
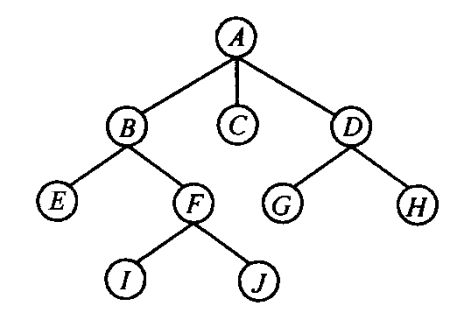
- 節點的度:一個結點的兒子結點個數稱為該節點的度
- 樹的度:一棵樹的度是指該樹中結點的最大度數。如上圖的樹的度是3
- 葉節點或終端節點:度為零的節點。如上圖中E,I,J,C,G,H是葉節點
- 非終端節點或分支節點:度不為零的節點。除根節點外的分支節點都叫做內部節點。
- 路徑:若存在樹中的一個節點序列k1,k2,…,kj,使得結點ki是ki+1的父結點(1<=i<j),則稱該結點序列是樹中從結點k1到結點kj的一條路徑。
-
路徑長度:路徑所經過的邊的數目。
-
節點高度:從該結點到各葉結點的最長路徑長度,例如上圖中B,C,D的高度分別是2,0,1
-
樹的高度:(這裡規定單根的高度為0)根結點的高度
-
結點的深度(或層數):從樹根到任一結點n有唯一的路徑,稱該路徑的長度為結點n的深度(或層數)。從根結點算起,根為第0層,它的孩子為第1層……
-
森林:m(m>=0)棵互不相交的樹的集合
樹的遍歷
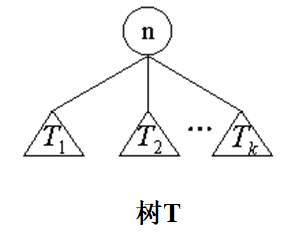
- 前序遍歷:先訪問樹根n,然後依次前序遍歷T1,T2,…,Tk。
- 中序遍歷:先中序遍歷T1,然後訪問樹根n,接著依次對T2,T3,…,Tk 進行中序遍歷。
- 後序遍歷:先依次對T1,T2,…,Tk進行後序遍歷,最後訪問樹根n。
樹的表示方法
- 父節點數組表示法

(1)樹中的結點數字化為它們的編號1,2,…,n。
(2)用一個一維數組存儲每個結點的父結點。即:father[k]中是存放結點k的父結點的編號。
(3)由於樹中每個結點的父結點是唯一的,所以父結點數組表示法可以唯一表示任何一棵樹。
- 兒子鏈表表示法
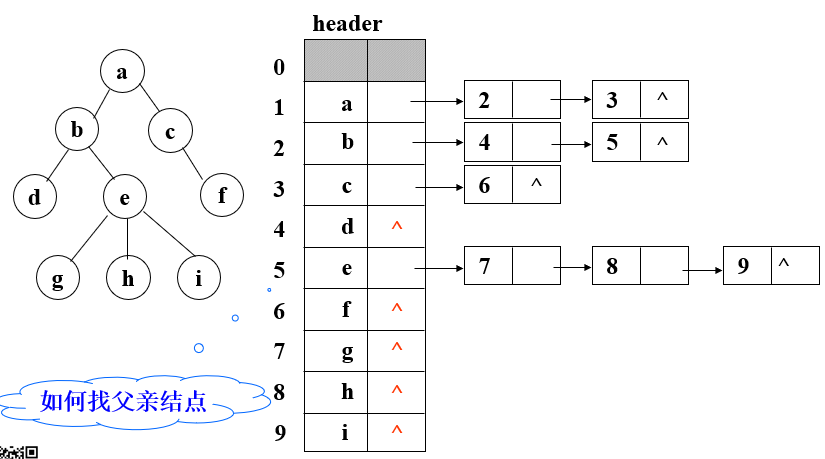
如果要查找父節點,可以再數組中添加一個parent域,用來存儲每個節點的父節點對應數組下標。
- 左兒子兄弟表示法
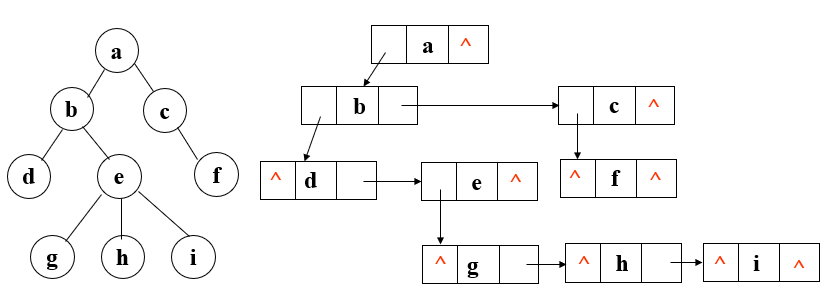
實現:用二叉鏈表作樹的存儲結構,鏈表中每個結點的兩個指針域分別指向其最左兒子和右鄰兄弟



