【解題報告】洛谷 P2571 [SCOI2010]傳送帶

【解題報告】洛谷 P2571 [SCOI2010]傳送帶
今天無聊，很久沒有做過題目了，但是又不想做什麼太難的題目，所以就用洛谷隨機跳題，跳到了一道題目，感覺好像不是太難。

[CSDN鏈接](https://blog.csdn.net/Liang_Si_FFF/article/details/84570359)
[題目鏈接](https://www.luogu.org/problemnew/show/P2571)

===================================================================================
題目描述

在一個2維平面上有兩條傳送帶，每一條傳送帶可以看成是一條線段。兩條傳送帶分別為線段AB和線段CD。lxhgww在AB上的移動速度為P，在CD上的移動速度為Q，在平面上的移動速度R。現在lxhgww想從A點走到D點，他想知道最少需要走多長時間

 輸入輸出格式

輸入格式：
輸入數據第一行是4個整數，表示A和B的坐標，分別為Ax，Ay，Bx，By

第二行是4個整數，表示C和D的坐標，分別為Cx，Cy，Dx，Dy

第三行是3個整數，分別是P，Q，R

輸出格式：
輸出數據為一行，表示lxhgww從A點走到D點的最短時間，保留到小數點後2位

 輸入輸出樣例

輸入樣例#1：
0 0 0 100
100 0 100 100
2 2 1
 輸出樣例#1：
136.60
說明

對於100%的數據，1<= Ax，Ay，Bx，By，Cx，Cy，Dx，Dy<=1000

1<=P，Q，R<=10

======================================================================================================

下麵是我的分析過程

分析過程

首先，如圖

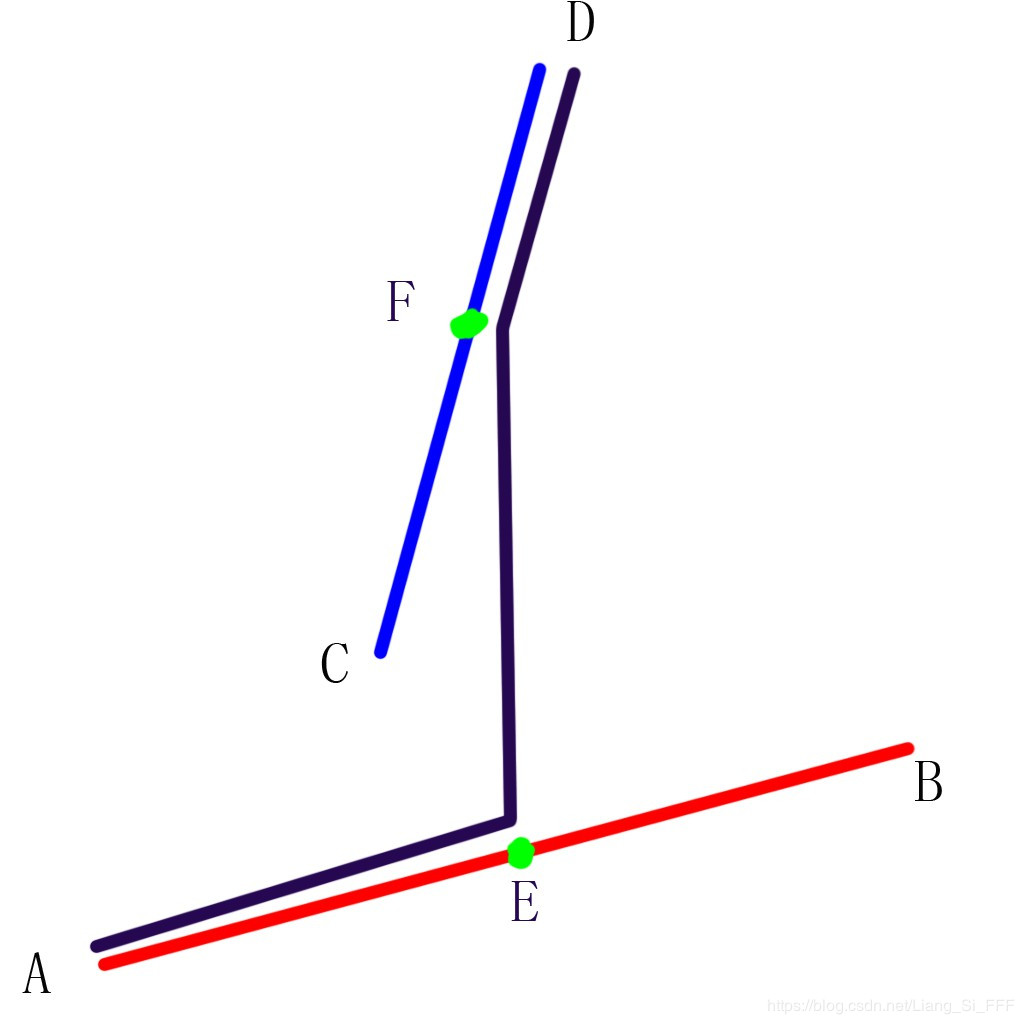
　　1. 通過觀察題目，我們可以發現，我們行走的路徑一定是先在AB邊上走，然後走下AB邊，走向CD邊，然後在CD邊上走。（當然，有可能直接在A點就走下了AB邊，也有可能直接從D點上了CD邊，這裡我們同樣看作是先走下AB邊，然後走上AB邊）所以如果我們在AB邊取一個點E,在CD邊取一個點F,那麼，不同的路徑就可以用不同的E點和F點唯一表示，即每一個數對(E,F)都唯一對應一條路徑（PS:E點可以和A或B重合，F點可以和C或者D重合）所以，我們可以想到一個朴素的演算法：枚舉E點和F點。但是這種演算法明顯是太暴力了，不可能通過的。
　　2. 我們通過仔細思考，可以這麼想：假如我現在的E點是已經確定好是哪個點的了，那麼我們的問題就可以轉換為：已知一條傳送帶，以及你在傳送帶上面的速度和地面上的速度，並且知道起點的準確位置，求到達終點的最短時間。
假如題目變成了這個樣子，那麼我們會發現，隨著F點從C點到D點移動，這個總的時間應該是先遞減後遞增的。由於是一個單峰函數，所以我們可以用三分來做。
　　3. 那麼，我們現在的問題就是，這個E點也是移動的。但是我們現在能夠做到對於AB邊上的每一個點E,都能算出E點固定時的最短時間。所以，相比剛剛開始的同時枚舉兩個點E和F，現在只需要枚舉一下E點就可以了。即：枚舉E點的位置，然後對於每一個E點，對F點進行三分，找出每一個E點對應的最小路徑的F點是哪一個。
　　4. 但是，這個演算法好像還是不太好，因為E點的枚舉還是很麻煩的，複雜度一樣很高。我們可以大膽猜想，或許E點的取值範圍也是可以用三分法來做的！但是我還沒有想到證明方法，也只是胡亂瞎猜。不過我猜對了。我還沒有找到證明，找到證明之後我會再貼鏈接或者幹啥的。
　　5. 所以，我們現在可以得出一個能夠在規定時間得出答案的演算法：先三分E點的位置，對於每一個E點的位置，再三分F點的位置。
（細節註意：由於答案要保留小數點後兩位，而地圖的最大大小為1000，經過測試，1000乘於2/3大概乘那麼30次就可以變得比0.01小，所以我們的三分大概只需要迴圈30次就可以了。不過我為了安全，迴圈了40次，反正沒差多少。因此，E點需要三分40次，對於每一個E點，需要三分F點40*2次，大概就320次的樣子。）
>事實上，這道題除了用三分的做法之外，好像還有什麼其他做法，比如模擬退火演算法， 但是我還沒有學過。
AC代碼如下

  1 #include<cstdio>
  2 #include<cmath>
  3 using namespace std;
  4 struct point
  5 {
  6 double x,y;
  7 point()
  8 {
  9 x=y=0;
 10 }
 11 };
 12 double m_abs(double a)
 13 {
 14 return a<0?-a:a;
 15 }
 16 int main()
 17 {
 18 point a,b,c,d;
 19 scanf("%lf%lf%lf%lf%lf%lf%lf%lf",&a.x,&a.y,&b.x,&b.y,&c.x,&c.y,&d.x,&d.y);
 20 double p,q,r;
 21 scanf("%lf%lf%lf",&p,&q,&r);
 22 double result=100000000.0;
 23 point S1=a,S2=b,E1=c,E2=d;
 24 for(int i=1;i<=40;i++)
 25 {
 26 point s1,s2;
 27 s1.x=S1.x+(S2.x-S1.x)/3.0;
 28 s1.y=S1.y+(S2.y-S1.y)/3.0;
 29 s2.x=S2.x-(S2.x-S1.x)/3.0;
 30 s2.y=S2.y-(S2.y-S1.y)/3.0;
 31 double T1,T2;
 32 double X,Y;
 33 X=m_abs(a.x-s1.x);
 34 Y=m_abs(a.y-s1.y);
 35 T1=sqrt(X*X+Y*Y)/p;
 36 X=m_abs(a.x-s2.x);
 37 Y=m_abs(a.y-s2.y);
 38 T2=sqrt(X*X+Y*Y)/p;
 39 E1=c;E2=d;
 40 double T3=10000000.0,T4=100000000.0;
 41 for(int j=1;j<=40;j++)
 42 {
 43 double t1,t2;
 44 point e1,e2;
 45 e1.x=E1.x+(E2.x-E1.x)/3.0;
 46 e1.y=E1.y+(E2.y-E1.y)/3.0;
 47 e2.x=E2.x-(E2.x-E1.x)/3.0;
 48 e2.y=E2.y-(E2.y-E1.y)/3.0;
 49 X=m_abs(s1.x-e1.x);
 50 Y=m_abs(s1.y-e1.y);
 51 t1=sqrt(X*X+Y*Y)/r;
 52 X=m_abs(s1.x-e2.x);
 53 Y=m_abs(s1.y-e2.y);
 54 t2=sqrt(X*X+Y*Y)/r;
 55 X=m_abs(d.x-e1.x);
 56 Y=m_abs(d.y-e1.y);
 57 t1+=sqrt(X*X+Y*Y)/q;
 58 X=m_abs(d.x-e2.x);
 59 Y=m_abs(d.y-e2.y);
 60 t2+=sqrt(X*X+Y*Y)/q;
 61 if(t1>=t2)
 62 {
 63 E1=e1;
 64 T3=t2<T3?t2:T3;
 65 }
 66 else
 67 {
 68 E2=e2;
 69 T3=t1<T3?t1:T3;
 70 }
 71 }
 72 E1=c;E2=d;
 73 for(int j=1;j<=40;j++)
 74 {
 75 double t1,t2;
 76 point e1,e2;
 77 e1.x=E1.x+(E2.x-E1.x)/3.0;
 78 e1.y=E1.y+(E2.y-E1.y)/3.0;
 79 e2.x=E2.x-(E2.x-E1.x)/3.0;
 80 e2.y=E2.y-(E2.y-E1.y)/3.0;
 81 X=m_abs(s2.x-e1.x);
 82 Y=m_abs(s2.y-e1.y);
 83 t1=sqrt(X*X+Y*Y)/r;
 84 X=m_abs(s2.x-e2.x);
 85 Y=m_abs(s2.y-e2.y);
 86 t2=sqrt(X*X+Y*Y)/r;
 87 X=m_abs(d.x-e1.x);
 88 Y=m_abs(d.y-e1.y);
 89 t1+=sqrt(X*X+Y*Y)/q;
 90 X=m_abs(d.x-e2.x);
 91 Y=m_abs(d.y-e2.y);
 92 t2+=sqrt(X*X+Y*Y)/q;
 93 if(t1>=t2)
 94 {
 95 E1=e1;
 96 T4=t2<T4?t2:T4;
 97 }
 98 else
 99 {
100 E2=e2;
101 T4=t1<T4?t1:T4;
102 }
103 }
104 T1+=T3;
105 T2+=T4;
106 if(T1>=T2)
107 {
108 S1=s1;
109 result=T2<result?T2:result;
110 }
111 else
112 {
113 S2=s2;
114 result=T1<result?T1:result;
115 }
116 }
117 printf("%.2f\n",result);
118 return 0;
119 }

話說這個還是我第一次使用三分呢，以前都沒有用過。