K：平衡二叉樹(AVL)

来源:https://www.cnblogs.com/MyStringIsNotNull/archive/2018/01/17/8306848.html
-Advertisement-
Play Games

相關介紹：  二叉查找樹的查找效率與二叉樹的形狀有關，對於按給定序列建立的二叉排序樹，若其左、右子樹均勻分佈，則查找過程類似於有序表的二分查找，時間複雜度變為O(log2n)。當若給定序列原來有序，則建立的二叉查找樹就蛻化為單鏈表，其查找效率同順序查找一樣，時間複雜度為O（n）。因此，在構 ...


相關介紹：

 二叉查找樹的查找效率與二叉樹的形狀有關，對於按給定序列建立的二叉排序樹，若其左、右子樹均勻分佈，則查找過程類似於有序表的二分查找，時間複雜度變為O(log2n)。當若給定序列原來有序，則建立的二叉查找樹就蛻化為單鏈表，其查找效率同順序查找一樣，時間複雜度為O（n）。因此，在構造二叉查找樹的過程中，當出現左右子樹分佈不均勻時，若能對其進行調整，使其依然保持均勻，則就能有效的保證二叉查找樹仍具有較高的查找效率。而平衡二叉樹，正是這樣的一棵樹。

 平衡二叉樹，又稱為AVL樹，它或是一棵空樹，或是一棵具有如下性質的二叉樹:它的左子樹和右子樹均為平衡二叉樹，且左子樹和右子樹深度之差的絕對值不超過1

 在平衡二叉樹上插入或刪除節點後，可能使二叉樹失去平衡。因此，需要對失去平衡的二叉樹進行調整，以保持平衡二叉樹的性質。以下，主要介紹如何動態地使一棵二叉查找樹保持平衡，即對失去平衡的二叉查找樹進行平衡化調整。這裡引入了平衡因數的概念。

 所謂的平衡因數，指的是二叉樹中某個節點的左子樹深度與右子樹深度之差，平衡因數也稱為平衡度。平衡二叉樹也就是樹中任意節點的平衡因數的絕對值小於等於1的二叉樹。在AVL樹中的節點的平衡因數有3種取值情況：1(左子樹深度大於右子樹深度)，0(左子樹深度等於右子樹深度)，-1(左子樹深度小於右子樹深度)

在以下給出的例子中，為了敘述方便，假設在AVL樹上因插入新節點而失去平衡的最小子樹的根節點為A，即A為距離插入節點最近的，平衡因數不是-1、0和1的節點。失去平衡後的操作可 依據失去平衡的原因(此處為便於記憶的訣竅的一個關鍵，如“LL型平衡旋轉”，指的是，在A的左孩子節點(L)的左孩子節點（L）中插入一個新的節點所導致的不平衡問題) 歸納為下列4種情況分別進行介紹：

  1. LL型平衡旋轉(單向右旋)：由於在A的左孩子的左子樹上插入新節點，使得A的平衡度由1增加至2，致使以A為根的子樹失去平衡。此時，應該進行一次向右的順時針旋轉操作，“提升”B（即為A的左孩子）為新子樹的根節點，A下降為B的右孩子，同時將B原來的右子樹B-R調整為A的左子樹。其過程如下圖所示：

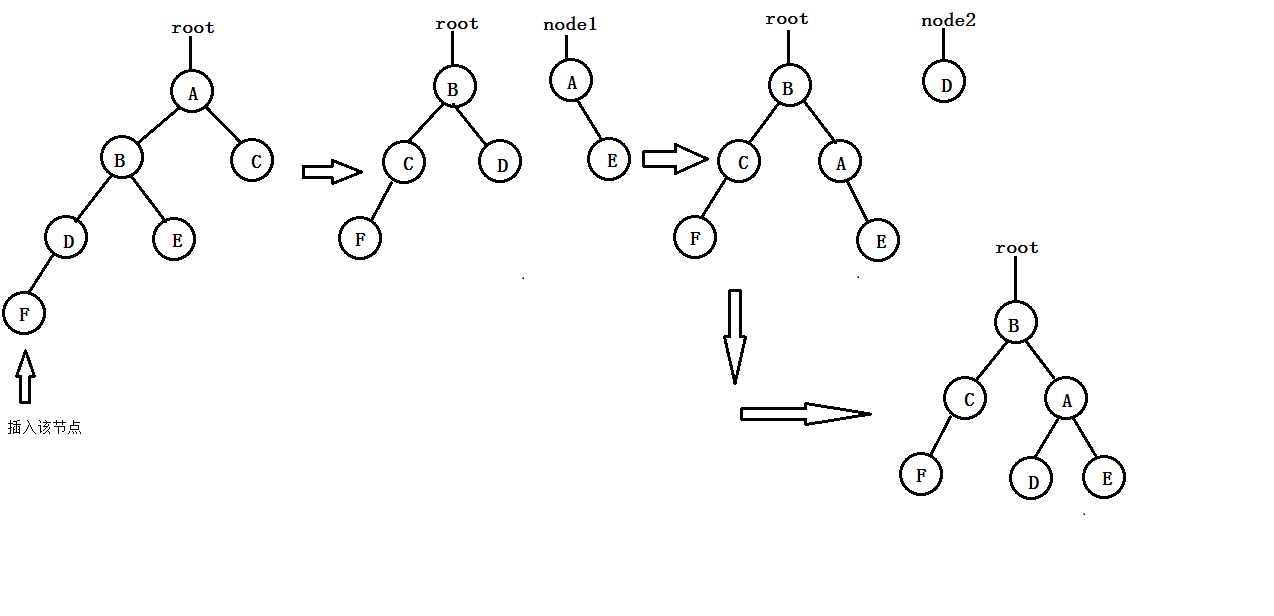
LL型平衡旋轉

  1. RR型平衡旋轉(單向左旋):由於在A的右孩子的右子樹上插入新節點，使得A的平衡度由-1轉變為-2，致使以A為根的子樹失去平衡。此時，應該進行一次的向左的逆時針旋轉操作，“提升”B(即A的右孩子)為新子樹的根節點，A下降為B的左子樹，同時將B原來的左子樹B-L調整為A的右子樹。其過程如下圖所示：

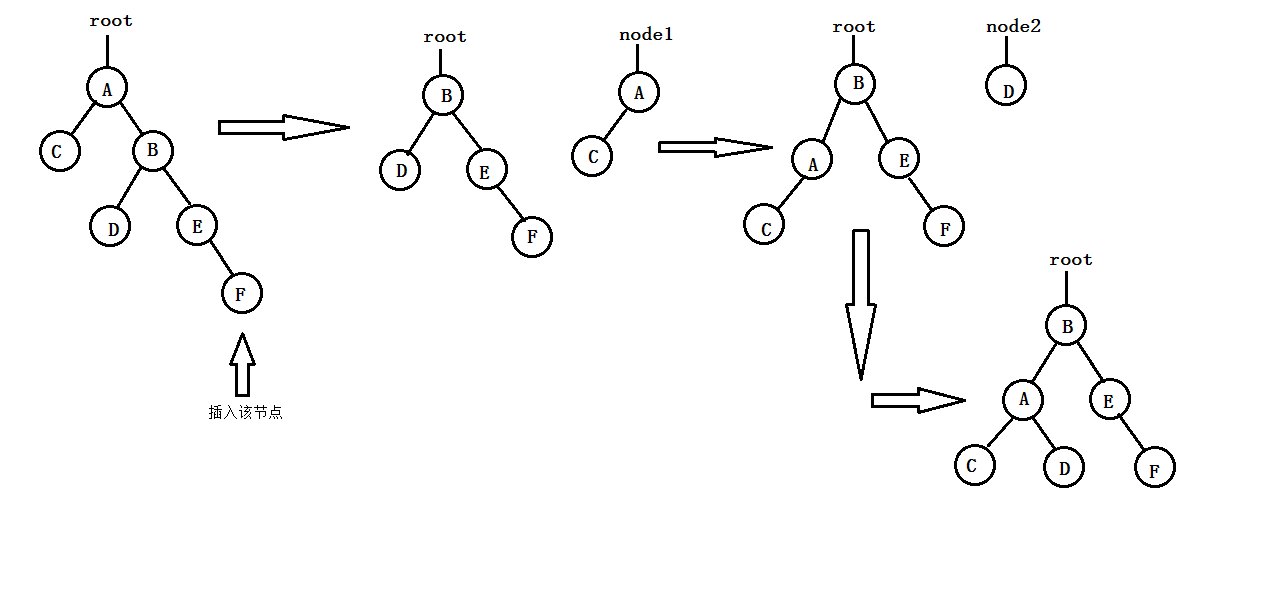
RR型平衡旋轉

  1. LR型平衡旋轉(先左旋後右旋)：由於在A的左孩子的右子樹上插入新節點，使得A的平衡度由1變為2，致使以A為根的子樹失去平衡。此時，應當進行兩次選裝操作（先逆時針，後順時針）“提升”C（即A的左孩子的右孩子）為新子樹的根節點；A下降為C的右孩子；B變為C的左孩子；C原來的左子樹C-L調整為B現在的右子樹；C原來的右子樹C-R調整為A的左子樹。其過程如下圖所示：

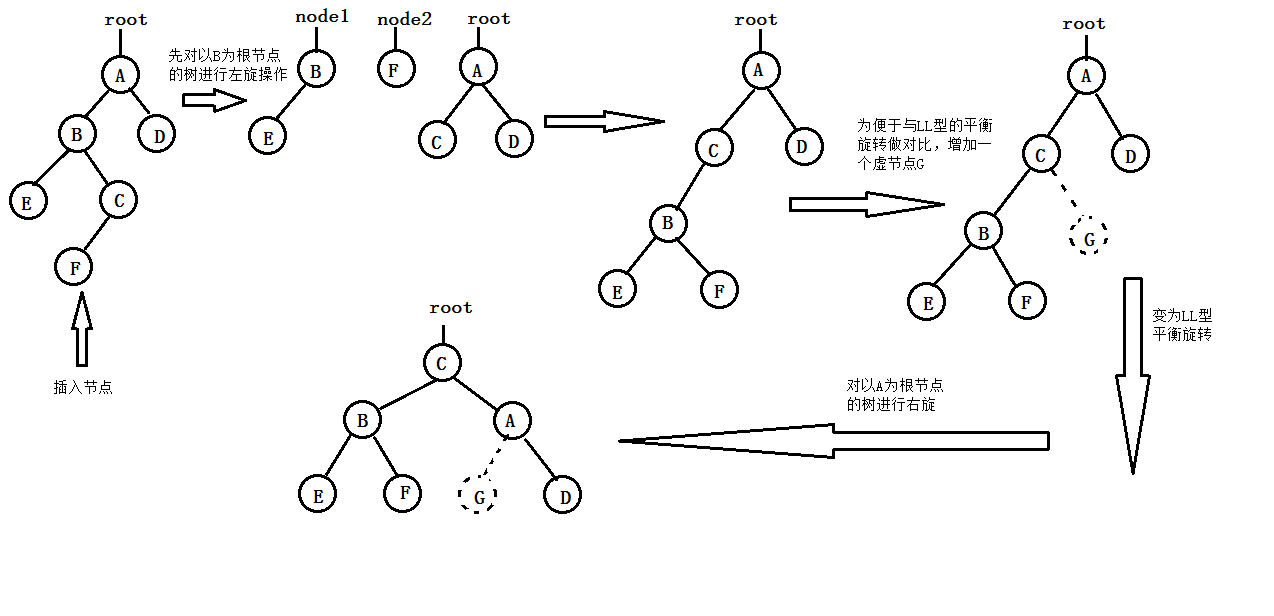
LR型平衡旋轉,變為B的右子樹

或

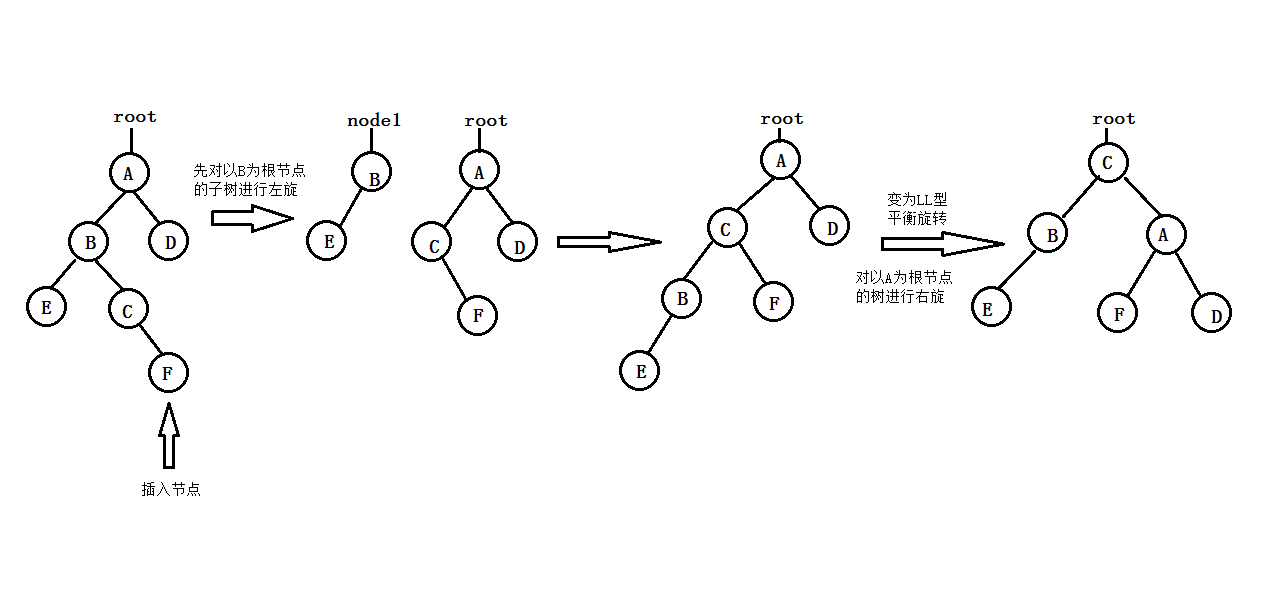
LR型平衡旋轉,變為A的左子樹

  1. RL型平衡旋轉（先右旋後左旋）：由於在A的右孩子的左子樹上插入新節點，使A的平衡度由-1變為-2，致使以A為根的子樹失去平衡，此時，應進行兩次旋轉操作（先順時針，後逆時針），“提升”C（即A的右孩子的左孩子）為新子樹的根節點；A下降為C的左孩子；B變為C的右孩子；C原來的左子樹C-L調整為A現在的右子樹；C原來的右子樹C-R調整為B的左子樹。其過程如下圖所示：

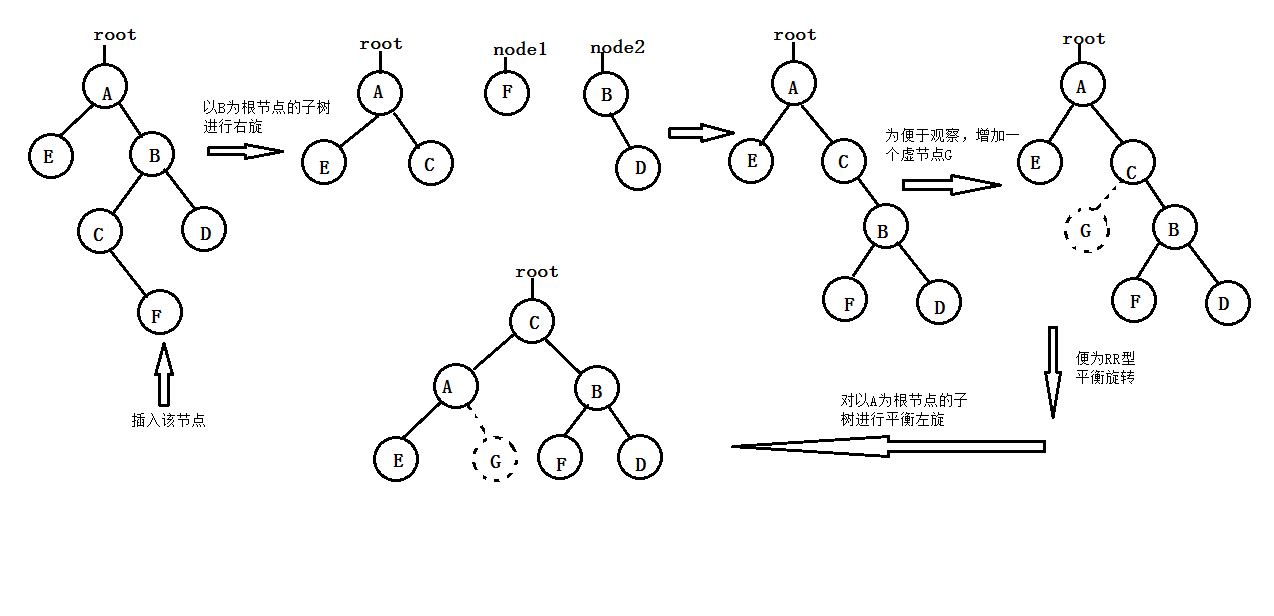
RL型平衡旋轉，變為B的左子樹

或

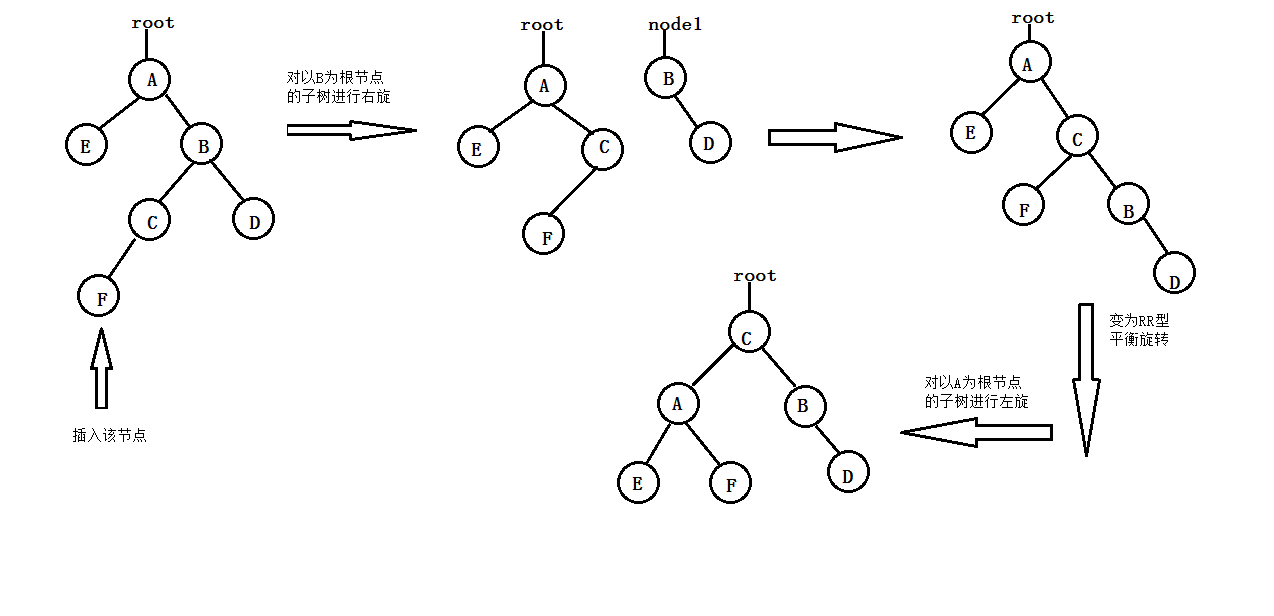
RL型平衡旋轉，變為A的右子樹

綜上所述：在平衡二叉查找樹T上插入一個新記錄x的演算法描述如下：

  1. 若AVL樹為空樹，則插入一個記錄為x的新節點作為T的根節點，樹的深度增加1。
  2. 若x的關鍵字值和AVL樹T的根節點的關鍵字值相等，則不進行插入操作。

  3. 若X的關鍵字值小於AVL樹的根節點的關鍵字值，則將x插入在該樹的左子樹上，並且當插入之後的左子樹深度增加1時，分別就下列不同情況進行處理：

    1. 若AVL樹的根節點的平衡因數為-1（右子樹的深度大於左子樹的深度），則將根節點的平衡因數調整為0，並且樹的深度不變

    2. 若AVL樹的根節點的平衡因數為0（左右子樹的深度相等）。則將根節點的平衡因數調整為1，樹的深度同時增加1

    3. 若AVL樹的根節點的平衡因數為1（左子樹的深度大於右子樹的深度），則當該樹的左子樹的根節點的平衡因數為1時需要進行LL型平衡旋轉；當該樹的左子樹的根節點的平衡因數為-1時需進行LR型平衡旋轉

  4. 若x的關鍵字值大於AVL樹的根節點的關鍵字值，則將x插入在該樹的右子樹上，並且當插入之後的右子樹深度增加1時，分別就下列不同情況進行處理：

    1. 若AVL樹的根節點的平衡因數為-1時（右子樹的深度大於左子樹的深度），則當該樹的右子樹的根節點的平衡因數為-1時需進行RR型平衡旋轉；當該樹的右子樹的根節點的平衡因數為1時需進行RL型平衡旋轉

    2.若AVL樹的根節點的平衡因數為0時（左右子樹的深度相等），則將根節點的平衡因數調整為-1，樹的深度同時增加1

    1. 若AVL樹的根節點的平衡因數為1時（左子樹的深度大於右子樹的深度），則將根節點的平衡因數調整為0，並且樹的深度保持不變

平衡二叉樹的優缺點分析：

優點：使二叉樹的結構更好(即不會出現“偏拐”嚴重的情況)，從而提高了查找操作的速度。

缺點：使插入和刪除操作複雜化，從而減低了插入和刪除操作的速度。

總結：平衡二叉樹適用於二叉查找樹一經建立就很少進行插入和刪除操作，而主要進行查找操作的應用場合上。由於其在查找過程中和給定值進行比較的關鍵字個數不超過樹的深度。因此，在平衡二叉樹上進行查找的時間複雜度為O（log2n）

相關操作示例代碼：

 對於平衡二叉樹，其常見的操作有插入、刪除、查找操作。其中，插入和刪除某個節點時，需要對失去平衡的平衡二叉查找樹進行相應的旋轉操作，以使平衡二叉樹保持結構上的穩定。

下麵代碼定義了平衡二叉查找樹的節點：

相關代碼：

/**
 * 該類用於定義平衡二叉樹的節點的相關數據
 * @author 學徒
 *
 */
class AVLTreeNode
{
    //節點的關鍵字
    Comparable key;
    //節點的數據
    Object data;
    //節點的左子樹指針
    AVLTreeNode left;
    //節點的右子樹指針
    AVLTreeNode right;
    
    public AVLTreeNode(Comparable key,Object data)
    {
        this(key,data,null,null);
    }
    public AVLTreeNode(Comparable key,Object data,AVLTreeNode left,AVLTreeNode right)
    {
        this.data=data;
        this.key=key;
        this.left=left;
        this.right=right;
    }
}

 對於查找操作，其先與根節點的關鍵字的值進行比較，根據比較所得的結果，選擇返回其相關的數據或者是遞歸的在該節點的左右子樹中進行查找

下麵代碼演示了查找的操作：

相關代碼：

/**
 * 用於平衡二叉樹中的查找操作，並返回相應節點的相關數據，當未查找到時，返回null
 * @param key 要進行查找的節點的關鍵字
 * @return 得到要進行查找節點的相關數據
 */
public Object search(Comparable key)
{
    if(key==null)
        return null;
    return getSearchResult(root,key);
}

/**
 * 用於輔助平衡二叉樹的查找操作，並返回相應的相關節點的數據，當未查找到時，返回null
 * @param root 要進行查找的二叉查找樹的根節點
 * @param key 要進行查找的節點的關鍵字
 * @return 得到要進行查找節點的相關數據
 */
private Object getSearchResult(AVLTreeNode root,Comparable key)
{
    if(root==null)
        return null;
    int compare=key.compareTo(root.key);
    if(compare==0)
        return root.data;
    else if(compare==1)
        return getSearchResult(root.right,key);
    else
        return getSearchResult(root.left,key);
}

 對於插入操作，先根據其關鍵字值的大小關係，在平衡二叉樹中插入相應的節點。之後，遍歷該新插入節點的路徑中各個根節點的平衡因數的情況，根據其平衡因數的值，選擇性的對其進行旋轉操作，需要註意的是在該路徑上最多只存在一次“失衡”的情況。為此，在對其路徑上的節點進行過旋轉操作之後，其平衡二叉樹整體便是處於“平衡”的狀態的

下麵代碼演示了插入操作：

相關代碼：

/**
 * 用於往二叉樹中插入新的節點
 * @param key 二叉樹中新節點的關鍵字
 * @param data 二叉樹中新節點的數據
 * @return 插入新節點的結果，如果成功插入一個新節點則返回true，否則返回false，當新增的節點存在於樹中時，返回false
 */
public boolean insert(Comparable key,Object data)
{
    if(key==null)
        return false;
    else if(root!=null)
    {
        return insertAVLTreeNode(root,null,key,data);
    }
    else
    {
        root=new AVLTreeNode(key,data);
        return true;
    }
}

/**
 * 輔助往二叉樹中插入新的節點
 * @param node 要進行比較的二叉樹的節點
 * @param parent 要進行比較的二叉樹的節點的父節點
  * @param key 新增節點的關鍵字值
 * @param data 新增節點的數據
 * @return 新增的結果
 */
private boolean insertAVLTreeNode(AVLTreeNode node,AVLTreeNode parent,Comparable key,Object data)
{
    //噹噹前比較的節點不為空的時候，進行比較操作
    if(node!=null)
    {
        int compare=key.compareTo(node.key);
        if(compare==0)
            return false;
        else if(compare>0)
            return insertAVLTreeNode(node.right,node,key,data);
        else
            return insertAVLTreeNode(node.left,node,key,data);
    }
    //當前的節點為空的時候，進行從其父節點處插入節點的操作。同時，進行旋轉判斷和相應的操作
    else
    {
        Comparable parentKey=parent.key;
        AVLTreeNode newNode=new AVLTreeNode(key,data);
        int comparable=parentKey.compareTo(key);
        //插入新增節點
        if(comparable>0)
            parent.left=newNode;
        else
            parent.right=newNode;
        //對插入完後的節點進行判斷，查看其是否需要進行旋轉操作，當需要時，對其進行進行旋轉調整平衡二叉樹相應的節點情況
        rotate(root,null,newNode);
        return true;
    }
}

 對於刪除操作，其只需要在二叉樹中找到要進行刪除的節點的父節點。之後移動相應的指針即可對其進行刪除操作，同時用其按照關鍵字有序的後繼節點對其進行補充即可，之後從對到其進行刪除節點的父節點的路徑上的所有節點進行遍歷，當存在因為刪除節點而導致其失去平衡的情況，則對其進行相應的平衡旋轉操作

下麵代碼演示了刪除操作：

相關代碼：

/**
 * 用於進行刪除操作
 * @param key 要進行刪除操作的節點的關鍵字值
 * @return 返回所刪除節點的數據值,當無相關的刪除節點的時候，返回null
 */
public Object delete(Comparable key)
{
    if(key==null)
        return null;
    else
        return remove(root,key,null);
}
/**
 * 用於輔助進行刪除操作的方法
 * @param node 當前比較節點
 * @param parent 當前比較節點的雙親節點
 * @param key 需要進行刪除的節點的關鍵字值
 * @return 返回所刪除節點的關鍵字
 */
public Object remove(AVLTreeNode node,Comparable key,AVLTreeNode parent)
{
    if (node != null)
    {
        int compare = key.compareTo(node.key);
        // 從左子樹中進行刪除
        if (compare < 0)
        {
            return remove(node.left, key, node);
        }
        // 從右子樹中進行刪除
        else if (compare > 0)
        {
            return remove(node.right, key, node);
        }
        // 當前節點即為要進行刪除的節點
        else
        {
            // 當前要進行刪除的節點的數據
            Object result = node.data;
            // 當前要進行刪除的節點的左右子樹均存在
            if (node.left != null && node.right != null)
            {
                // 尋找要進行刪除節點的替換節點
                AVLTreeNode innext = node.right;
                //要進行替換的節點的雙親節點
                AVLTreeNode innextParent=node;
                // 尋找右子樹下的最左孩子節點
                while (innext.left != null)
                {
                    innextParent=innext;
                    innext = innext.left;
                }
                // 改變刪除節點的相關數據
                node.data = innext.data;
                node.key = innext.key;
                //遞歸的刪除其進行替換的節點  
                remove(node.right,innext.key,node);
                //對從當前被刪除節點開始的到其相應的替換節點的父節點的路徑上判斷其是否“失衡”且進行相關的旋轉操作
                rotate(node,null,innextParent);
            }
            // 以下考慮的情況均當前刪除節點缺少左子樹或者右子樹的情況
            else
            {
                // 當前要進行刪除的節點不為根節點的時候
                if (parent != null)
                {
                    // 當左子樹不為空的時候
                    if (node.left != null && node.right == null)
                    {
                        // 當前節點為其左子樹節點的時候
                        if (node == parent.left)
                        {
                            parent.left = node.left;
                        }
                        // 當前節點為其右子樹節點的時候
                        else
                        {
                            parent.right = node.left;
                        }
                        if(node.left!=null)
                        {
                            //由於其刪除節點缺少左子樹或者右子樹。為此，其只需判斷當前刪除節點的父節點的失衡情況併進行相應的調整即可
                            rotate(parent,null,node.left);
                        }
                    }
                    // 當右子樹不為空的時候或為葉子節點的時候
                    else
                    {
                        // 當前節點為其左子樹節點的時候
                        if (node == parent.left)
                        {
                            parent.left = node.right;
                        }
                        // 當前節點為其右子樹節點的時候
                        else
                        {
                            parent.right = node.right;
                        }
                        if(node.right!=null)
                        {
                            //由於其刪除節點缺少左子樹或者右子樹。為此，其只需判斷當前刪除節點的父節點的失衡情況併進行相應的調整即可
                            rotate(parent,null,node.right);
                        }
                    }
                    
                }
                // 當前刪除的節點為根節點的時候
                else
                {
                    if (node.left != null)
                        root = node.left;
                    else
                        root = node.right;
                }
            }
            // 返回其進行刪除的節點的值
            return result;
        }
    }
    return null;
}

完整示例代碼如下：

相關代碼：

package all_in_tree;
/**
 * 該類用於演示平衡二叉樹的相關操作
 * @author 學徒
 *
 */
public class AVLTree
{
    //該平衡二叉樹的根節點
    private AVLTreeNode root;
    
    /**
     * 對該平衡二叉樹進行後續遍歷操作(後序遍歷的結果是按序排序的)，以便用於驗證其測試的結果
     */
    public static void inTravel(AVLTreeNode root)
    {
        if(root!=null)
        {
            inTravel(root.left);
            System.out.print(root.key+"-"+root.data+"\t");
            inTravel(root.right);
            
        }
    }
    
    /**
     * 用於獲取該平衡二叉樹
     * @return 該平衡二叉樹的根節點指針
     */
    public AVLTreeNode getTree()
    {
        return this.root;
    }
    
    /**
     * 用於得到一棵以root為根節點的樹的深度
     * @param root 需要獲取的樹的深度的根節點指針
     * @return 以root為根節點的樹的深度
     */
    private int getDepth(AVLTreeNode root)
    {
        if(root==null)
            return 0;
        return Math.max(getDepth(root.left),getDepth(root.right))+1;
    }
    
    /**
     * 用於判斷以root為根節點的二叉樹的平衡情況，true為平衡的，false表示並不平衡
     * @param root 要判斷其平衡因數的子樹的根節點指針
     * @return 以root為根節點的平衡二叉樹的平衡情況
     */
    private boolean isBalance(AVLTreeNode root)
    {
        return Math.abs(getDepth(root.left)-getDepth(root.right))<=1;
    }
    
    /**
     * 用於獲取以root為根節點的二叉樹的平衡因數
     * @param root為求取其平衡因數的子樹的根節點的指針
     * @return 平衡因數
     */
    private int getBalance(AVLTreeNode root)
    {
        return getDepth(root.left)-getDepth(root.right);
    }
    
    /**
     * 用於平衡二叉樹中的查找操作，並返回相應節點的相關數據，當未查找到時，返回null
     * @param key 要進行查找的節點的關鍵字
     * @return 得到要進行查找節點的相關數據
     */
    public Object search(Comparable key)
    {
        if(key==null)
            return null;
        return getSearchResult(root,key);
    }
    
    /**
     * 用於輔助平衡二叉樹的查找操作，並返回相應的相關節點的數據，當未查找到時，返回null
     * @param root 要進行查找的二叉查找樹的根節點
     * @param key 要進行查找的節點的關鍵字
     * @return 得到要進行查找節點的相關數據
     */
    private Object getSearchResult(AVLTreeNode root,Comparable key)
    {
        if(root==null)
            return null;
        int compare=key.compareTo(root.key);
        if(compare==0)
            return root.data;
        else if(compare==1)
            return getSearchResult(root.right,key);
        else
            return getSearchResult(root.left,key);
    }
    
    /**
     * 以所傳入的節點的指針為根節點的二叉樹，進行右旋的操作
     * @param node 要進行右旋的二叉樹的根節點
     * @return 旋轉後的二叉樹的根節點的指針
     */
    private AVLTreeNode rightRotate(AVLTreeNode node)
    {
        //用於記錄旋轉後的結果
        AVLTreeNode result=node.left;
        node.left=result.right;
        result.right=node;
        return result;
    }
    
    /**
     * 以所傳入的節點的指針為根節點的二叉樹，進行左旋的操作
     * @param node 要進行左旋的二叉樹的根節點
     * @return 旋轉後的二叉樹的根節點的指針
     */
    private AVLTreeNode leftRotate(AVLTreeNode node)
    {
        //用於記錄旋轉後的結果
        AVLTreeNode result=node.right;
        node.right=result.left;
        result.left=node;
        return result;
    }
    
    /**
     * 用於往二叉樹中插入新的節點
     * @param key 二叉樹中新節點的關鍵字
     * @param data 二叉樹中新節點的數據
     * @return 插入新節點的結果，如果成功插入一個新節點則返回true，否則返回false，當新增的節點存在於樹中時，返回false
     */
    public boolean insert(Comparable key,Object data)
    {
        if(key==null)
            return false;
        else if(root!=null)
        {
            return insertAVLTreeNode(root,null,key,data);
        }
        else
        {
            root=new AVLTreeNode(key,data);
            return true;
        }
    }
    
    /**
     * 輔助往二叉樹中插入新的節點
     * @param node 要進行比較的二叉樹的節點
     * @param parent 要進行比較的二叉樹的節點的父節點
     * @param key 新增節點的關鍵字值
     * @param data 新增節點的數據
     * @return 新增的結果
     */
    private boolean insertAVLTreeNode(AVLTreeNode node,AVLTreeNode parent,Comparable key,Object data)
    {
        //噹噹前比較的節點不為空的時候，進行比較操作
        if(node!=null)
        {
            int compare=key.compareTo(node.key);
            if(compare==0)
                return false;
            else if(compare>0)
                return insertAVLTreeNode(node.right,node,key,data);
            else
                return insertAVLTreeNode(node.left,node,key,data);
        }
        //當前的節點為空的時候，進行從其父節點處插入節點的操作。同時，進行旋轉判斷和相應的操作
        else
        {
            Comparable parentKey=parent.key;
            AVLTreeNode newNode=new AVLTreeNode(key,data);
            int comparable=parentKey.compareTo(key);
            //插入新增節點
            if(comparable>0)
                parent.left=newNode;
            else
                parent.right=newNode;
            //對插入完後的節點進行判斷，查看其是否需要進行旋轉操作，當需要時，對其進行進行旋轉調整平衡二叉樹相應的節點情況
            rotate(root,null,newNode);
            return true;
        }
    }
    
    /**
     * 用於輔助新插入節點是否旋轉的判斷，並作出相應的操作
     * @param root 當前查找的節點的情況
     * @param parent 當前查找節點的雙親節點
     * @param node 進行旋轉操作的路徑的終止節點
     */
    private void rotate(AVLTreeNode root,AVLTreeNode parent,AVLTreeNode node)
    {
        //由此得出當前查找節點的查找方向
        int compare=root.key.compareTo(node.key);
        //當找到該新增節點的時候，其路徑上的各個節點的平衡因數均不“失衡”則直接進行返回,不進行操作
        if(compare==0)
        {
            return;
        }
        //當平衡且當前節點的關鍵字值小於新增節點的關鍵字值的時候，往右邊進行查找
        else if(compare<0&&isBalance(root))
        {
            //當其路徑上的根節點平衡的時候，往右邊查找
            rotate(root.right,root,node);
        }
        //當平衡且當前節點的關鍵字值大於新增節點的關鍵字值的時候，往左邊進行查找
        else if(compare>0&&isBalance(root))
        {
            //當其路徑上的子樹的根節點平衡的時候，往左邊進行查找
            rotate(root.left,root,node);
        }
        //當失衡的時候，對其進行旋轉操作
        else 
        {
            //當其父節點為null的時候，不需要對其進行旋轉操作，因為此時表示樹中的節點數目不超過3個，所以一定不會有失衡的情況產生
            if(parent!=null)
            {
                //當其失衡的時候，對其進行旋轉操作
                //用於判斷是從其父節點的左邊失衡的還是右邊
                boolean isLeft=parent.left.key.compareTo(root.key)==0?true:false;
                //用於獲取該失衡節點的平衡因數
                int balance=getBalance(root);
                //大於0的時候，要麼進行LL型旋轉，要麼進行LR型旋轉
                if(balance>0)
                {
                    //用於獲取其孩子節點的平衡因數，根據其平衡因數的情況，進行相應的旋轉操作
                    int childBalance=getBalance(root.left);
                    //對其相應的孩子節點為根節點的子樹進行左旋
                    if(childBalance<0)
                    {
                        root.left=leftRotate(root.left);
                    }
                    //對以失衡的樹的根節點為子樹的樹進行右旋操作
                    AVLTreeNode rotateNode=rightRotate(root);
                    if(isLeft)
                        parent.left=rotateNode;
                    else
                        parent.right=rotateNode;
                }
                //小於0的時候，要麼進行RR型旋轉，要麼進行RL型旋轉
                else
                {
                    //用於獲取其孩子節點的平衡因數，根據其平衡因數的情況，進行相應的旋轉操作
                    int childBalance=getBalance(root.right);
                    //對其相應的孩子節點為根的子樹進行右旋
                    if(childBalance>0)
                    {
                        root.right=rightRotate(root.right);
                    }
                    //對以失衡的樹的根節點為子樹的樹進行左旋操作
                    AVLTreeNode rotateNode=leftRotate(root);
                    if(isLeft)
                        parent.left=rotateNode;
                    else
                        parent.right=rotateNode;
                }
            }
        }
    }
    
    /**
     * 用於進行刪除操作
     * @param key 要進行刪除操作的節點的關鍵字值
     * @return 返回所刪除節點的數據值,當無相關的刪除節點的時候，返回null
     */
    public Object delete(Comparable key)
    {
        if(key==null)
            return null;
        else
            return remove(root,key,null);
    }
    /**
     * 用於輔助進行刪除操作的方法
     * @param node 當前比較節點
     * @param parent 當前比較節點的雙親節點
     * @param key 需要進行刪除的節點的關鍵字值
     * @return 返回所刪除節點的關鍵字
     */
    public Object remove(AVLTreeNode node,Comparable key,AVLTreeNode parent)
    {
        if (node != null)
        {
            int compare = key.compareTo(node.key);
            // 從左子樹中進行刪除
            if (compare < 0)
            {
                return remove(node.left, key, node);
            }
            // 從右子樹中進行刪除
            else if (compare > 0)
            {
                return remove(node.right, key, node);
            }
            // 當前節點即為要進行刪除的節點
            else
            {
                // 當前要進行刪除的節點的數據
                Object result = node.data;
                // 當前要進行刪除的節點的左右子樹均存在
                if (node.left != null && node.right != null)
                {
                    // 尋找要進行刪除節點的替換節點
                    AVLTreeNode innext = node.right;
                    //要進行替換的節點的雙親節點
                    AVLTreeNode innextParent=node;
                    // 尋找右子樹下的最左孩子節點
                    while (innext.left != null)
                    {
                        innextParent=innext;
                        innext = innext.left;
                    }
                    // 改變刪除節點的相關數據
                    node.data = innext.data;
                    node.key = innext.key;
                    //遞歸的刪除其進行替換的節點  
                    remove(node.right,innext.key,node);
                    //對從當前被刪除節點開始的到其相應的替換節點的父節點的路徑上判斷其是否“失衡”且進行相關的旋轉操作
                    rotate(node,null,innextParent);
                }
                // 以下考慮的情況均當前刪除節點缺少左子樹或者右子樹的情況
                else
                {
                    // 當前要進行刪除的節點不為根節點的時候
                    if (parent != null)
                    {
                        // 當左子樹不為空的時候
                        if (node.left != null && node.right == null)
                        {
                            // 當前節點為其左子樹節點的時候
                            if (node == parent.left)
                            {
                                parent.left = node.left;
                            }
                            // 當前節點為其右子樹節點的時候
                            else
                            {
                                parent.right = node.left;
                            }
                            if(node.left!=null)
                            {
                                //由於其刪除節點缺少左子樹或者右子樹。為此，其只需判斷當前刪除節點的父節點的失衡情況併進行相應的調整即可
                                rotate(parent,null,node.left);
                            }
                        }
                        // 當右子樹不為空的時候或為葉子節點的時候
                        else
                        {
                            // 當前節點為其左子樹節點的時候
                            if (node == parent.left)
                            {
                                parent.left = node.right;
                            }
                            // 當前節點為其右子樹節點的時候
                            else
                            {
                                parent.right = node.right;
                            }
                            if(node.right!=null)
                            {
                                //由於其刪除節點缺少左子樹或者右子樹。為此，其只需判斷當前刪除節點的父節點的失衡情況併進行相應的調整即可
                                rotate(parent,null,node.right);
                            }
                        }
                        
                    }
                    // 當前刪除的節點為根節點的時候
                    else
                    {
                        if (node.left != null)
                            root = node.left;
                        else
                            root = node.right;
                    }
                }
                // 返回其進行刪除的節點的值
                return result;
            }
        }
        return null;
    }
    
    /**
     * 測試用例
     * @param args 初始化參數數組
     */
    public static void main(String[] args)
    {
        AVLTree tree=new AVLTree();
        tree.insert(5,"A");
        tree.insert(2,"B");
        tree.insert(6,"D");
        tree.insert(1,"E");
        tree.insert(3,"C");
        tree.insert(4,"F");
        AVLTree.inTravel(tree.getTree());
        System.out.println();
        System.out.println(tree.delete(1));
        AVLTree.inTravel(tree.getTree());
        System.out.println();
        System.out.println(tree.search(5));
    }
}


運行結果如下：

1-E 2-B 3-C 4-F 5-A 6-D 
E
2-B 3-C 4-F 5-A 6-D 
A

其測試用例所用圖如下：

完整代碼測試用例圖

回到目錄|·(工)·）


您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • 國際化資源管理模塊重構總結
    從17年末到18年初花了差不多三周的時間，將項目中最重要的模塊之一--國際化資源管理，進行了徹底的重構。在掉了無數頭髮加了好多個晚上的班之後，終於改變了先前一個service解決所有邏輯的臃腫情況，代碼的可讀性，擴展性，模塊功能的擴展性以及可用性等性能獲得了很大的提升。我在這次重構中有著許許多多的思 ...
  • 設計模式複習小結一(Strategy Pattern/Observer Pattern/Decorator Patter/Factory Pattern)
    目錄： 前言 1. Stratrgy Pattern 2. Observer Pattern 3. Decorator Pattern 4. Factory Pattern 4.1 FactoryPattern 4.2 AbstractFactoryPattern 總結 4.1 FactoryPat ...
  • 設計模式（六大原則之單一職責）
    概念：就一個類而言，應該僅有一個引起它變化的原因 描述的意思是每個類都只負責單一的功能，切不可太多，並且一個類應當儘量的把一個功能做到極致。如果一個類承擔的職責過多，就等於把這些職責耦合在一起，這種耦合會導致脆弱的設計，即當其中一個職責發生變化時將會影響這個類完成其它職責的功能。以下代碼就沒有遵守該 ...
  • Java集合系列[3]----HashMap源碼分析
    前面我們已經分析了ArrayList和LinkedList這兩個集合，我們知道ArrayList是基於數組實現的，LinkedList是基於鏈表實現的。它們各自有自己的優劣勢，例如ArrayList在定位查找元素時會優於LinkedList，而LinkedList在添加刪除元素時會優於ArrayLi ...
  • XML DTD語法瞭解
    dtd語法 元素： <!Element 元素名稱 數據類型|包含內容> 數據類型： #PCDATA：普通文本 使用的時候一般用()引起來 包含內容： 該元素下可以出現哪些元素， 用()引起來 符號： * 出現任意次 ？ 出現1次或者0次 + 出現至少1次 | 或者 () 分組 ， 順序 屬性： 格式 ...
  • R語言學習筆記（二十二）：字元串處理中的函數對比
    字元串處理中基本函數的使用 R自帶函數與stringr包函數對比 ...
  • 最笨的方法解賊簡單的題
    題目：輸入一個5x5矩陣，將其中最大的元素移到中心，4個角分別放4個最小的元素（順序從左到右，從上到下以此從小到大存放） 思路：最大值是最好找的，迴圈遍歷一次，找出最大值和其地址。然後就是找最小的那4個數字，我的思路是首先用一數組來存放二維數組的第一行，然後從第二行開始遍歷，從該數組b中最大的元素開 ...
  • python網路編程（進程與多線程）
    multiprocessing模塊 由於GIL的存在，python中的多線程其實並不是真正的多線程，如果想要充分地使用多核CPU的資源，在python中大部分情況需要使用多進程。 multiprocessing包是Python中的多進程管理包。與threading.Thread類似，它可以利用mul ...
一周排行
    -Advertisement-
    Play Games
  • 移動開發（一）：使用.NET MAUI開發第一個安卓APP
    移動開發（一）：使用.NET MAUI開發第一個安卓APP 對於工作多年的C#程式員來說，近來想嘗試開發一款安卓APP，考慮了很久最終選擇使用.NET MAUI這個微軟官方的框架來嘗試體驗開發安卓APP，畢竟是使用Visual Studio開發工具，使用起來也比較的順手，結合微軟官方的教程進行了安卓 ...
  • wpf ToggleButton選中效果和一個登錄界面
    前言 QuestPDF 是一個開源 .NET 庫，用於生成 PDF 文檔。使用了C# Fluent API方式可簡化開發、減少錯誤並提高工作效率。利用它可以輕鬆生成 PDF 報告、發票、導出文件等。 項目介紹 QuestPDF 是一個革命性的開源 .NET 庫，它徹底改變了我們生成 PDF 文檔的方 ...
  • 彈幕樹洞項目功能新增篇
    項目地址 項目後端地址： https://github.com/ZyPLJ/ZYTteeHole 項目前端頁面地址： ZyPLJ/TreeHoleVue (github.com) https://github.com/ZyPLJ/TreeHoleVue 目前項目測試訪問地址： http://tree ...
  • 第27篇 sqlserver2022詳細安裝步驟
    話不多說，直接開乾 一.下載 1.官方鏈接下載： https://www.microsoft.com/zh-cn/sql-server/sql-server-downloads 2.在下載目錄中找到下麵這個小的安裝包 SQL2022-SSEI-Dev.exe，運行開始下載SQL server； 二. ...
  • .NET 開源高性能 MQTT 類庫
    前言 隨著物聯網（IoT）技術的迅猛發展，MQTT（消息隊列遙測傳輸）協議憑藉其輕量級和高效性，已成為眾多物聯網應用的首選通信標準。 MQTTnet 作為一個高性能的 .NET 開源庫，為 .NET 平臺上的 MQTT 客戶端與伺服器開發提供了強大的支持。 本文將全面介紹 MQTTnet 的核心功能 ...
  • Serilog文檔翻譯系列（六） - 可用的接收器、增強器、格式化輸出
    Serilog支持多種接收器用於日誌存儲，增強器用於添加屬性，LogContext管理動態屬性，支持多種輸出格式包括純文本、JSON及ExpressionTemplate。還提供了自定義格式化選項，適用於不同需求。 ...
  • 警惕 Visual Studio 屬性求值副作用導致邏輯不符合預期
    目錄簡介獲取 HTML 文檔解析 HTML 文檔測試參考文章 簡介 動態內容網站使用 JavaScript 腳本動態檢索和渲染數據，爬取信息時需要模擬瀏覽器行為，否則獲取到的源碼基本是空的。 本文使用的爬取步驟如下： 使用 Selenium 獲取渲染後的 HTML 文檔 使用 HtmlAgility ...
  • [使用目前最新版]HybridCLR6.9.0+YooAsset2.2.4實現純C# Unity熱更新方案 (一)
    1.前言 什麼是熱更新 游戲或者軟體更新時，無需重新下載客戶端進行安裝，而是在應用程式啟動的情況下，在內部進行資源或者代碼更新 Unity目前常用熱更新解決方案 HybridCLR，Xlua，ILRuntime等 Unity目前常用資源管理解決方案 AssetBundles，Addressable， ...
  • 在 ASP.NET Core Web API 中使用操作篩選器統一處理通用操作
    本文章主要是在C# ASP.NET Core Web API框架實現向手機發送驗證碼簡訊功能。這裡我選擇是一個互億無線簡訊驗證碼平臺，其實像阿裡雲，騰訊雲上面也可以。 首先我們先去 互億無線 https://www.ihuyi.com/api/sms.html 去註冊一個賬號 註冊完成賬號後，它會送 ...
  • 第28篇 如何.net中實現高效可靠數據同步api
    通過以下方式可以高效，並保證數據同步的可靠性 1.API設計 使用RESTful設計，確保API端點明確，並使用適當的HTTP方法（如POST用於創建，PUT用於更新）。 設計清晰的請求和響應模型，以確保客戶端能夠理解預期格式。 2.數據驗證 在伺服器端進行嚴格的數據驗證，確保接收到的數據符合預期格 ...
所有分類