洛谷題目傳送門

題目

題目描述

曾經有一款流行的游戲，叫做 Infinity Loop，先來簡單的介紹一下這個游戲：
游戲在一個 n ∗ m 的網格狀棋盤上進行，其中有些小方格中會有水管，水管可能在格子某些方向的邊界的中點有介面，所有水管的粗細都相同，所以如果兩個相鄰方格的共邊界的中點都有接頭，那麼可以看作這兩個接頭互相連接。水管有以下 15 種形狀：

游戲開始時，棋盤中水管可能存在漏水的地方。
形式化地：如果存在某個接頭，沒有和其它接頭相連接，那麼它就是一個漏水的地方。
玩家可以進行一種操作：選定一個含有非直線型水管的方格，將其中的水管繞方格中心順時針或逆時針旋轉 90 度。
直線型水管是指左圖裡中間一行的兩種水管。
現給出一個初始局面，請問最少進行多少次操作可以使棋盤上不存在漏水的地方。

輸入輸出格式

輸入格式：

第一行兩個正整數 n， m，代表網格的大小。
接下來 n 行每行 m 個數，每個數是 [0,15] 中的一個，你可以將其看作一個 4 位的二進位數，從低到高每一位分別代表初始局面中這個格子上、右、下、左方向上是否有水管接頭。
特別地，如果這個數是 0 ，則意味著這個位置沒有水管。
比如 3(0011(2)) 代表上和右有接頭，也就是一個 L 型;
而 12(1100(2)) 代表下和左有接頭，也就是將 L 型旋轉 180 度。

輸出格式：

輸出共一行，表示最少操作次數。如果無法達成目標，輸出-1.

輸入輸出樣例

輸入樣例#1：

2 3
3 14 12
3 11 12

輸出樣例#1：

2

輸入樣例#2：

3 2
1 8
5 10
2 4

輸出樣例#2：

-1

輸入樣例#3：

3 3
9 11 3
13 15 7
12 14 6

輸出樣例#3：

16

說明

【樣例 1 解釋】

樣例 1 棋盤如下
旋轉方法很顯然，先將左上角虛線方格內的水管順時針轉 90 度

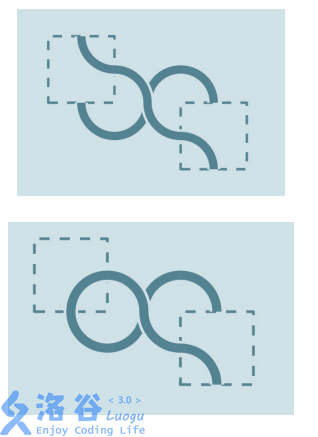
然後右下角虛線方格內的水管逆時針旋轉 90 度，這樣就使得水管封閉了

【樣例 2 解釋】

樣例 2 為題目描述中的第一張圖片，無法達成目標。

【樣例 3 解釋】

樣例 3 為題目描述中的第二張圖片，將除了中心方格以外的每個方格內的水管都轉 180 度即可。

思路分析

表示這是一道思維神題。。。。。。
有人第一眼看上去覺得這要跑費用流嗎？
然而只要會建圖，剩下的就是套模板的事了。

我們這樣來理解。對於每個方格上的水管的每一個支管，有且僅有一個其它方格上的支管與其相連，這樣就不會漏水了。用網路流知識表述，就是每個支管容量只能為1，且全都要滿流，於是跑最小費用可行流。

然而即使產生了最優情況，整個管網也不一定是一整個聯通塊，而可能被分成若幹塊。因此，怎樣強制使每兩個相鄰的方格上都產生流量呢？就要把源匯點連到每個格子上。而且，還要對每個格點染色，相鄰的兩個格點，一個連源點，一個連匯點。具體的實現，就要利用格點行列坐標和的奇偶性來判斷。

而產生的費用呢？當然是旋轉造成的啦！真正的思維就體現在這裡了。因為旋轉還會造成接觸點的變化，所以肯定是要拆點的，一個方格拆成五個點，上下左右中。。。。。。中間點連上源/匯點，並根據支管情況向四周連容量1，費用0的邊。四周視作接觸點，與對應相鄰的另一個接觸點連容量1，費用0的邊。討論相鄰兩個方格格因旋轉而產生的有費用的連邊，實在是太難了。。。。。。猛然發現，所有的情況，其實只需要在內部進行轉化就好了。

所有的方格，我們大致分成以下幾類進行討論。

第一種：射線型

這種好辦。射線指向上面，那麼就讓左、下、右接觸點直接連接上接觸點。左，右連上去，表示只要轉90度，所以費用為1。下麵連上去費用為2。

第二種：直角型

這種理解起來就有難度了。如果順時針轉90度，會變成這樣

相當於原來連上接觸點的支管連到了下麵，那麼上與下建一條容量為1，費用為1的邊。同樣的道理，逆時針轉90度，左與右建一條容量為1，費用為1的邊。再來討論轉180度，這時候，會通過已有的邊由左、下直接轉移到右、上，費用加起來正好是2，所以不用連更多邊了。

第三種：T字型

像前面一樣討論，也可以建邊。從下向左、右各建一條容量為1，費用為1的邊，向上建一條費用為2的邊。這裡就留給讀者自己思考啦。

以上三種情況，每一種都有4個形狀，但連邊方法都是一樣的。
還有直線型，十字型和空的，要麼不能轉，要麼轉了沒意義，就不用內部建邊了。

下麵貼代碼

#include<cstdio>
#include<cstdlib>
#include<cstring>
using namespace std;
#define R register int
#define UP(U) U+turn*sum
#define RI(U) U+((turn+1)&3)*sum
#define DO(U) U+((turn+2)&3)*sum
#define LE(U) U+((turn+3)&3)*sum
#define MD(U) U+(sum<<2)//上面幾個用來計算對應點的數組下標，上下左右中。。。
const int INF=2147483647,N=20009,M=200009;
int sum,P=1,S=0,T;//sum方格總數，P建圖迴圈變數，S、T為源匯點
int he[N],ne[M],to[M],f[M],c[M];//f流量，c費用
int q[N],d[N],pre[N];//q隊列，d距離，pre記錄最短路
bool inq[N];//標記是否在隊列中
inline void in(R&z)//快讀
{
    register char c=getchar();
    while(c<'-')c=getchar();
    z=c&15;c=getchar();
    while(c>'-')z*=10,z+=c&15,c=getchar();
}
inline void add(R u,R v,R flow,R cost,R tp)//建邊，tp表示染色屬性
{
    if(tp){tp=u;u=v;v=tp;}//如果是奇數點，所有的邊都要反向，要流出去
    to[++P]=v;ne[P]=he[u];he[u]=P;c[P]=cost;f[P]=flow;
    to[++P]=u;ne[P]=he[v];he[v]=P;c[P]=-cost;
}
#define PB(X) q[t]=X;if(++t==N)t=0
#define PF(X) if(--h<0)h=N-1;q[h]=v//手打了一下雙向迴圈隊列
inline bool spfa()//模板，加了兩種優化
{
    R h=0,t=1,i,u,v,dn,cnt=1,sum=0;
    for(i=S+1;i<=T;++i)d[i]=INF;
    q[0]=S;inq[0]=1;
    while(h!=t)
    {
        u=q[h];
        if(++h==N)h=0;
        if(d[u]*cnt>sum){PB(u);continue;}//LLL優化
        --cnt;sum-=d[u];
        for(i=he[u];i;i=ne[i])
            if(f[i]&&d[v=to[i]]>(dn=d[u]+c[i]))
            {
                if(inq[v])sum-=d[v];
                else
                {
                    inq[v]=1;++cnt;
                    if(d[v]<d[q[h]]){PB(v);}
                    else{PF(v);}//SLF優化
                }
                pre[v]=i;
                sum+=(d[v]=dn);
            }
        inq[u]=0;
    }
    return d[T]!=INF;
}
int main()
{
    R n,m,i,j,k=1,t,shape,turn,totf=0,mf=0,mc=0;//totf總流量，mf最大可行流，mc總費用
    in(n);in(m);
    sum=n*m;T=sum*5+1;
    for(i=0;i<n;++i)
        for(j=0;j<m;++j,++k)
        {
            turn=0;//turn下麵會用來翻轉，將同類型的水管歸類到一起
            t=(i+j)&1;//t是染色屬性，只要判斷奇偶
            if(t)add(S,MD(k),INF,0,0);
            else add(MD(k),T,INF,0,0);
            if(i)add(DO(k-m),UP(k),1,0,t);
            if(j)add(RI(k-1),LE(k),1,0,t);
            in(shape);
            if(shape&1)add(UP(k),MD(k),1,0,t),++totf;//統計總流量
            if(shape&2)add(RI(k),MD(k),1,0,t),++totf;//因為每個流拆成了兩段
            if(shape&4)add(DO(k),MD(k),1,0,t),++totf;//所以最終結果會是實際的兩倍
            if(shape&8)add(LE(k),MD(k),1,0,t),++totf;//中點與四周點連邊
            switch(shape)
            {
            case 8:++turn;//1000 ←
            case 4:++turn;//0100 ↓
            case 2:++turn;//0010 →
            case 1:       //0001 ↑
                add(RI(k),UP(k),1,1,t);
                add(DO(k),UP(k),1,2,t);
                add(LE(k),UP(k),1,1,t);
                break;//四種形狀內部連邊情況是一樣的，轉一下統一處理就方便些了，下麵同理
            case 9:++turn; //1001 ┘
            case 12:++turn;//1100 ┐
            case 6:++turn; //0110 ┌
            case 3:        //0011 └
                add(DO(k),UP(k),1,1,t);
                add(LE(k),RI(k),1,1,t);
                break;
            case 13:++turn;//1101 ┤
            case 14:++turn;//1110 ┬
            case 7:++turn; //0111 ├
            case 11:       //1011 ┴
                add(DO(k),LE(k),1,1,t);
                add(DO(k),UP(k),1,2,t);
                add(DO(k),RI(k),1,1,t);
                break;
            }
        }
    while(spfa())
    {
        m=INF;//這裡m記下流量
        for(i=T;i!=S;i=to[k^1])
        {
            k=pre[i];
            if(m>f[k])m=f[k];
        }
        mf+=m;
        for(i=T;i!=S;i=to[k^1])
        {
            k=pre[i];
            f[k]-=m;f[k^1]+=m;
            mc+=m*c[k];
        }
    }
    printf("%d",totf==mf<<1?mc:-1);//註意如果沒能流滿就輸-1
    return 0;
}