[1]數據結構 [2]二叉樹 [3]樹的遍歷 [4]樹的搜索 [5]自平衡樹 ...
前面的話
前面介紹過一種非順序數據結構是散列表,本文將詳細介紹另一種非順序數據結構——樹,它對於存儲需要快速查找的數據非常有用
數據結構
樹是一種分層數據的抽象模型。現實生活中最常見的樹的例子是家譜,或是公司的組織架構圖
一個樹結構包含一系列存在父子關係的節點。每個節點都有一個父節點(除了頂部的第一個 節點)以及零個或多個子節點
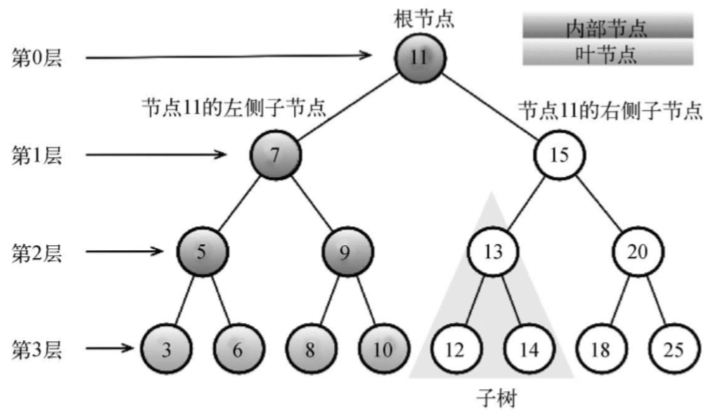
位於樹頂部的節點叫作根節點(11)。它沒有父節點。樹中的每個元素都叫作節點,節點分為內部節點和外部節點。至少有一個子節點的節點稱為內部節點(7、5、9、15、13和20是內部節點)。沒有子元素的節點稱為外部節點或葉節點(3、6、8、10、12、14、18和25是葉節點)。
一個節點可以有祖先和後代。一個節點(除了根節點)的祖先包括父節點、祖父節點、曾祖父節點等。一個節點的後代包括子節點、孫子節點、曾孫節點等。例如,節點5的祖先有節點7和節點11,後代有節點3和節點6。
有關樹的另一個術語是子樹。子樹由節點和它的後代構成。例如,節點13、12和14構成了上圖中樹的一棵子樹。
節點的一個屬性是深度,節點的深度取決於它的祖先節點的數量。比如,節點3有3個祖先節點(5、7和11),它的深度為3。
樹的高度取決於所有節點深度的最大值。一棵樹也可以被分解成層級。根節點在第0層,它的子節點在第1層,以此類推。上圖中的樹的高度為3(最大高度已在圖中表示——第3層)
二叉樹
二叉樹中的節點最多只能有兩個子節點:一個是左側子節點,另一個是右側子節點。這些定義有助於我們寫出更高效的向/從樹中插入、查找和刪除節點的演算法。二叉樹在電腦科學中的應用非常廣泛。
二叉搜索樹(BST)是二叉樹的一種,但是它只允許你在左側節點存儲(比父節點)小的值,在右側節點存儲(比父節點)大(或者等於)的值。上面的圖中就展現了一棵二叉搜索樹
【創建BinarySearchTree類】
現在開始創建自己的BinarySearchTree類。首先,聲明它的結構:
function BinarySearchTree() { var Node = function(key){ //{1} this.key = key; this.left = null; this.right = null; }; var root = null; //{2} }
下圖展現了二叉搜索樹數據結構的組織方式:
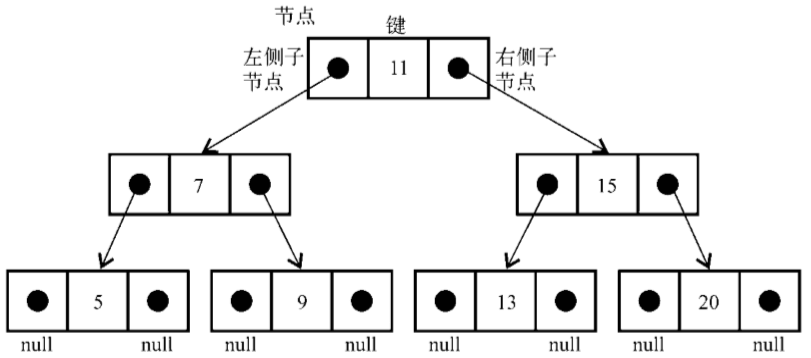
和鏈表一樣,將通過指針來表示節點之間的關係(術語稱其為邊)。在雙向鏈表中,每個節點包含兩個指針,一個指向下一個節點,另一個指向上一個節點。對於樹,使用同樣的方式(也使用兩個指針)。但是,一個指向左側子節點,另一個指向右側子節點。因此,將聲明一個Node類來表示樹中的每個節點(行{1})。值得註意的一個小細節是,不同於將節點本身稱作節點或項,我們將會稱其為鍵。鍵是樹相關的術語中對節點的稱呼。
我們將會遵循和LinkedList類中相同的模式,這表示也將聲明一個變數以控制此數據結構的第一個節點。在樹中,它不再是頭節點,而是根元素(行{2})。然後,我們需要實現一些方法。下麵是將要在樹類中實現的方法
insert(key):向樹中插入一個新的鍵。 search(key):在樹中查找一個鍵,如果節點存在,則返回true;如果不存在,則返回 false。 inOrderTraverse:通過中序遍歷方式遍歷所有節點。 preOrderTraverse:通過先序遍歷方式遍歷所有節點。 postOrderTraverse:通過後序遍歷方式遍歷所有節點。 min:返回樹中最小的值/鍵。 max:返回樹中最大的值/鍵。 remove(key):從樹中移除某個鍵。
【insert】
下麵的代碼是用來向樹插入一個新鍵的演算法的第一部分:
this.insert = function(key){ var newNode = new Node(key); //{1} if (root === null){ //{2} root = newNode; } else { insertNode(root,newNode); //{3} } };
要向樹中插入一個新的節點(或項),要經歷三個步驟
第一步是創建用來表示新節點的Node類實例(行{1})。只需要向構造函數傳遞我們想用來插入樹的節點值,它的左指針和右指針的值會由構造函數自動設置為null
第二步要驗證這個插入操作是否為一種特殊情況。這個特殊情況就是我們要插入的節點是樹的第一個節點(行{2})。如果是,就將根節點指向新節點
第三步是將節點加在非根節點的其他位置。這種情況下,需要一個私有的輔助函數(行{3}),函數定義如下:
var insertNode = function(node, newNode){ if (newNode.key < node.key){ //{4} if (node.left === null){ //{5} node.left = newNode; //{6} } else { insertNode(node.left, newNode); //{7} } } else { if (node.right === null){ //{8} node.right = newNode; //{9} } else { insertNode(node.right, newNode); //{10} } } };
insertNode函數會幫助我們找到新節點應該插入的正確位置。下麵是這個函數實現的步驟
1、如果樹非空,需要找到插入新節點的位置。因此,在調用insertNode方法時要通過參數傳入樹的根節點和要插入的節點
2、如果新節點的鍵小於當前節點的鍵(現在,當前節點就是根節點)(行{4}),那麼需要檢查當前節點的左側子節點。如果它沒有左側子節點(行{5}),就在那裡插入新的節點。如果有左側子節點,需要通過遞歸調用insertNode方法(行{7})繼續找到樹的下一層。在這裡,下次將要比較的節點將會是當前節點的左側子節點
3、如果節點的鍵比當前節點的鍵大,同時當前節點沒有右側子節點(行{8}),就在那裡插入新的節點(行{9})。如果有右側子節點,同樣需要遞歸調用insertNode方法,但是要用來和新節點比較的節點將會是右側子節點
考慮下麵的情景:我們有一個新的樹,並且想要向它插入第一個值
var tree = new BinarySearchTree(); tree.insert(11);
這種情況下,樹中有一個單獨的節點,根指針將會指向它。源代碼的行{2}將會執行。現在,來考慮下圖所示樹結構的情況:
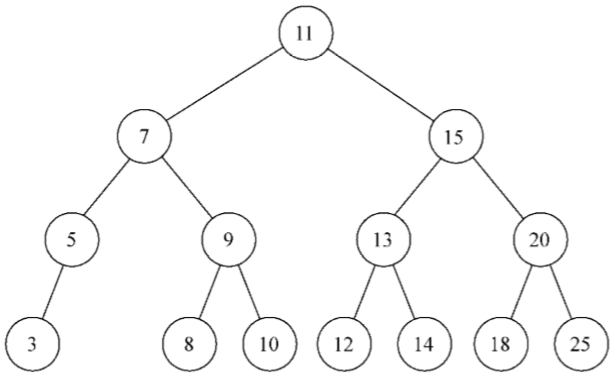
創建上圖所示的樹的代碼如下,它們接著上面一段代碼(插入了鍵為11的節點)之後輸入執行:
tree.insert(7); tree.insert(15); tree.insert(5); tree.insert(3); tree.insert(9); tree.insert(8); tree.insert(10); tree.insert(13); tree.insert(12); tree.insert(14); tree.insert(20); tree.insert(18); tree.insert(25);
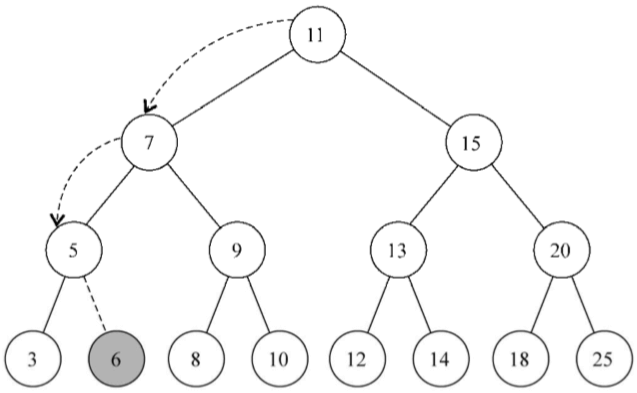
同時我們想要插入一個值為6的鍵,執行下麵的代碼:
tree.insert(6);
下麵的步驟將會被執行
1、樹不是空的,行{3}的代碼將會執行。insertNode方法將會被調用(root, key[6])
2、演算法將會檢測行{4}(key[6] < root[11]為真),並繼續檢測行{5}(node.left[7]不是null),然後將到達行{7}並調用insertNode(node.left[7], key[6])
3、將再次進入insertNode方法內部,但是使用了不同的參數。它會再次檢測行{4}(key[6] < node[7]為真),然後再檢測行{5}(node.left[5]不是null),接著到達行{7},調用insertNode(node.left[5], key[6])
4、將再一次進入insertNode方法內部。它會再次檢測行{4}(key[6] < node[5]為假), 然後到達行{8}(node.right是null——節點5沒有任何右側的子節點),然後將會執行行{9}, 在節點5的右側子節點位置插入鍵6
5、然後,方法調用會依次出棧,代碼執行過程結束
這是插入鍵6後的結果:
樹的遍歷
遍歷一棵樹是指訪問樹的每個節點並對它們進行某種操作的過程。但是我們應該怎麼去做呢?應該從樹的頂端還是底端開始呢?從左開始還是從右開始呢?訪問樹的所有節點有三種方式:中序、先序和後序。下麵將詳細介紹這三種遍歷方式的用法和實現
【中序遍歷】
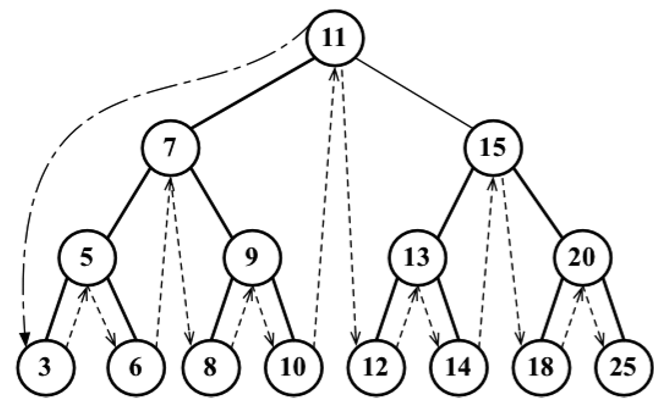
中序遍歷是一種以上行順序訪問BST所有節點的遍歷方式,也就是以從最小到最大的順序訪問所有節點。中序遍歷的一種應用就是對樹進行排序操作。我們來看它的實現:
this.inOrderTraverse = function(callback){ inOrderTraverseNode(root, callback); //{1} };
inOrderTraverse方法接收一個回調函數作為參數。回調函數用來定義我們對遍歷到的每個節點進行的操作(這也叫作訪問者模式)。由於我們在BST中最常實現的演算法是遞歸,這裡使用了一個私有的輔助函數,來接收一個節點和對應的回調函數作為參數(行{1})
var inOrderTraverseNode = function (node, callback) { if (node !== null) { //{2} inOrderTraverseNode(node.left, callback); //{3} callback(node.key); //{4} inOrderTraverseNode(node.right, callback); //{5} } };
要通過中序遍歷的方法遍歷一棵樹,首先要檢查以參數形式傳入的節點是否為null(這就是停止遞歸繼續執行的判斷條件——行{2}——遞歸演算法的基本條件)。然後,遞歸調用相同的函數來訪問左側子節點(行{3})。接著對這個節點進行一些操作(callback),然後再訪問右側子節點(行{5})
試著在之前展示的樹上執行下麵的方法:
function printNode(value){//{6}
console.log(value);
}
tree.inOrderTraverse(printNode);//{7}
但首先,需要創建一個回調函數(行{6})。要做的是在瀏覽器的控制臺上輸出節點的值。然後,調用inOrderTraverse方法並將回調函數作為參數傳入(行{7})。當執行上面的代碼後,下麵的結果將會在控制臺上輸出(每個數字將會輸出在不同的行):
3 5 6 7 8 9 10 11 12 13 14 15 18 20 25
下麵的圖描繪了inOrderTraverse方法的訪問路徑:
【先序遍歷】
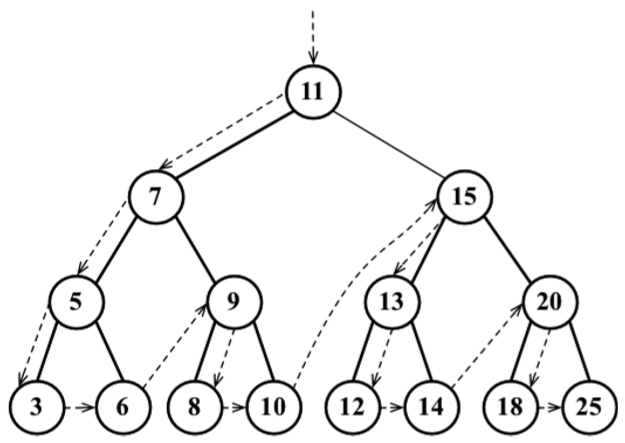
先序遍歷是以優先於後代節點的順序訪問每個節點的。先序遍歷的一種應用是列印一個結構化的文檔。下麵來看實現:
this.preOrderTraverse = function(callback){ preOrderTraverseNode(root, callback); };
preOrderTraverseNode方法的實現如下:
var preOrderTraverseNode = function (node, callback) { if (node !== null) { callback(node.key); //{1} preOrderTraverseNode(node.left, callback); //{2} preOrderTraverseNode(node.right, callback); //{3} } };
先序遍歷和中序遍歷的不同點是,先序遍歷會先訪問節點本身(行{1}),然後再訪問它的左側子節點(行{2}),最後是右側子節點(行{3}),而中序遍歷的執行順序是:{2}、{1}和{3}
下麵是控制臺上的輸出結果(每個數字將會輸出在不同的行):
11 7 5 3 6 9 8 10 15 13 12 14 20 18 25
下麵的圖描繪了preOrderTraverse方法的訪問路徑:
【後序遍歷】
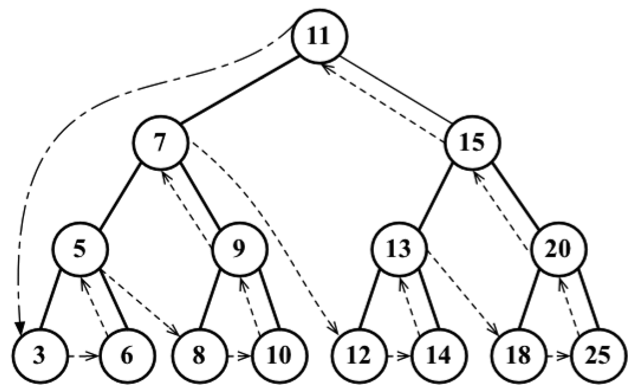
後序遍歷則是先訪問節點的後代節點,再訪問節點本身。後序遍歷的一種應用是計算一個目錄和它的子目錄中所有文件所占空間的大小。下麵來看它的實現:
this.postOrderTraverse = function(callback){ postOrderTraverseNode(root, callback); };
postOrderTraverseNode方法的實現如下:
var postOrderTraverseNode = function (node, callback) { if (node !== null) { postOrderTraverseNode(node.left, callback); //{1} postOrderTraverseNode(node.right, callback); //{2} callback(node.key); //{3} } };
這個例子中,後序遍歷會先訪問左側子節點(行{1}),然後是右側子節點(行{2}),最後是父節點本身(行{3})
中序、先序和後序遍歷的實現方式是很相似的,唯一不同的是行{1}、{2}和{3} 的執行順序。下麵是控制台的輸出結果(每個數字將會輸出在不同行):
3 6 5 8 10 9 7 12 14 13 18 25 20 15 11
樹的搜索
在樹中,有三種經常執行的搜索類型:1、最小值;2、最大值;3、搜索特定的值。下麵將詳細介紹這三種搜索類型
【最值】
使用下麵的樹作為示例:
如果看一眼樹最後一層最左側的節點,會發現它的值為3,這是這棵樹中最小的鍵。如果再看一眼樹最右端的節點(同樣是樹的最後一層),會發現它的值為25,這是這棵樹中最大的鍵。這條信息在我們實現搜索樹節點的最小值和最大值的方法時能給予我們很大的幫助
首先來看尋找樹的最小鍵的方法:
this.min = function() { return minNode(root); //{1} };
min方法將會暴露給用戶。這個方法調用了minNode方法(行{1}):
var minNode = function (node) { if (node){ while (node && node.left !== null) { //{2} node = node.left; //{3} } return node.key; } return null; //{4} };
minNode方法允許我們從樹中任意一個節點開始尋找最小的鍵。我們可以使用它來找到一棵樹或它的子樹中最小的鍵。因此,我們在調用minNode方法的時候傳入樹的根節點(行{1}),因為我們想要找到整棵樹的最小鍵。在minNode內部,我們會遍歷樹的左邊(行{2}和行{3})直到找到樹的最下層(最左端)
以相似的方式,可以實現max方法:
this.max = function() { return maxNode(root); }; var maxNode = function (node) { if (node){ while (node && node.right !== null) { //{5} node = node.right; } return node.key; } return null; };
要找到最大的鍵,我們要沿著樹的右邊進行遍歷(行{5})直到找到最右端的節點。 因此,對於尋找最小值,總是沿著樹的左邊;而對於尋找最大值,總是沿著樹的右邊
【特定值】
下麵來看搜索特定值的實現
this.search = function(key){ return searchNode(root, key); //{1} }; var searchNode = function(node, key){ if (node === null){ //{2} return false; } if (key < node.key){ //{3} return searchNode(node.left, key); //{4} } else if (key > node.key){ //{5} return searchNode(node.right, key); //{6} } else { return true; //{7} } };
我們要做的第一件事,是聲明search方法。和BST中聲明的其他方法的模式相同,我們將會使用一個輔助函數(行{1})。searchNode方法可以用來尋找一棵樹或它的任意子樹中的一個特定的值。這也是為什麼在行{1}中調用它的時候傳入樹的根節點作為參數。
在開始演算法之前,先要驗證作為參數傳入的node是否合法(不是null)。如果是null的話,說明要找的鍵沒有找到,返回false。如果傳入的節點不是null,需要繼續驗證。如果要找的鍵比當前的節點小(行{3}),那麼繼續在左側的子樹上搜索(行{4})。如果要找的鍵比當前的節點大,那麼就從右側子節點開始繼續搜索(行{6}),否則就說明要找的鍵和當前節點的鍵相等,就返回true來表示找到了這個鍵(行{7})。
可以通過下麵的代碼來測試這個方法:
console.log(tree.search(1) ? 'Key 1 found.' : 'Key 1 not found.');
console.log(tree.search(8) ? 'Key 8 found.' : 'Key 8 not found.');
輸出結果如下:
Value 1 not found. Value 8 found.
下麵來詳細介紹查找1這個鍵的時候方法是如何執行的
1、調用searchNode方法,傳入根節點作為參數(行{1})。(node[root[11]])不是null(行{2}),因此我們執行到行{3}
2、(key[1]<node[11])為ture(行{3}),因此來到行{4}並再次調用searchNode方法,傳入(node[7],key[1])作為參數
3、(node[7])不是null({2}),因此繼續執行行{3}
4、(key[1]<node[7])為ture(行{3}),因此來到行{4}並再次調用searchNode方法,傳入(node[5],key[1])作為參數
5、(node[5])不是null(行{2}),因此繼續執行行{3}
6、(key[1]<node[5])為ture(行{3}),因此來到行{4}並再次調用searchNode方法,傳入(node[3],key[1])作為參數
7、(node[3])不是null(行{2}),因此來到行{3}
8、(key[1]<node[3])為真(行{3}),因此來到行{4}並再次調用searchNode方法,傳入(null,key[1])作為參數。null被作為參數傳入是因為node[3]是一個葉節點(它沒有子節點,所以它的左側子節點的值為null)
9、節點(null)的值為null(行{2},這時要搜索的節點為null),因此返回false
10、然後,方法調用會依次出棧,代碼執行過程結束
下麵再來查找值為8的節點:
1、調用searchNode方法,傳入root作為參數(行{1})。(node[root[11]])不是null(行{2}),因此我們來到行{3}
2、(key[8]<node[11])為真(行{3}),因此執行到行{4}並再次調用searchNode方法,傳入(node[7],key[8])作為參數。(node[7])不是null,因此來到行{3}
3、(key[8]<node[7])為假(行{3}),因此來到行{5}
4、(key[8]>node[7])為真(行{5}),因此來到行{6}並再次調用searchNode方法,傳入(node[9],key[8])作為參數。(node[9])不是null(行{2}),因此來到行{3}
5、(key[8]<node[9])為真(行{3}),因此來到行{4}並再次調用searchNode方法,傳入(node[8],key[8])作為參數。(node[8])不是null(行{2}),因此來到行{3}
6、(key[8]<node[8])為假(行{3}),因此來到行{5}
7、(key[8]>node[8])為假(行{5}),因此來到行{7}並返回true,因為node[8]就是要找的鍵
8、然後,方法調用會依次出棧,代碼執行過程結束
【移除一個節點】
先創建這個remove方法,使它能夠在樹的實例上被調用
this.remove = function(key){ root = removeNode(root, key); //{1} };
這個方法接收要移除的鍵並且它調用了removeNode方法,傳入root和要移除的鍵作為參數(行{1})。要註意的是,root被賦值為removeNode方法的返回值
removeNode方法的複雜之處在於我們要處理不同的運行場景,當然也包括它同樣是通過遞歸來實現的。下麵來看removeNode方法的實現:
var removeNode = function(node, key){ if (node === null){ //{2} return null; } if (key < node.key){ //{3} node.left = removeNode(node.left, key); //{4} return node; //{5} } else if (key > node.key){ //{6} node.right = removeNode(node.right, key); //{7} return node; //{8} } else { //鍵等於node.key //第一種情況——一個葉節點 if (node.left === null && node.right === null){ //{9} node = null; //{10} return node; //{11} } //第二種情況——一個只有一個子節點的節點 if (node.left === null){ //{12} node = node.right; //{13} return node; //{14} } else if (node.right === null){ //{15} node = node.left; //{16} return node; //{17} } //第三種情況——一個有兩個子節點的節點 var aux = findMinNode(node.right); //{18} node.key = aux.key; //{19} node.right = removeNode(node.right, aux.key); //{20} return node; //{21} } };
下麵來看行{2},如果正在檢測的節點是null,那麼說明鍵不存在於樹中,所以返回null。然後要做的第一件事,就是在樹中找到要移除的節點。因此,如果要找的鍵比當前節點的值小(行{3}),就沿著樹的左邊找到下一個節點(行{4})。如果要找的鍵比當前節點的值大(行{6}),那麼就沿著樹的右邊找到下一個節點(行{7})。如果找到了要找的鍵(鍵和node.key相等),就需要處理三種不同的情況
findMinNode方法如下:
var findMinNode = function(node){ while (node && node.left !== null) { node = node.left; } return node; };
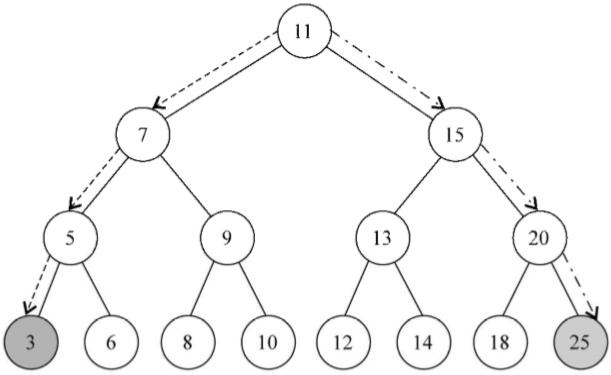
1、移除一個葉節點
第一種情況是該節點是一個沒有左側或右側子節點的葉節點——行{9}。在這種情況下,要做的就是給這個節點賦予null值來移除它(行{9})。但是僅僅賦一個null值是不夠的,還需要處理指針。在這裡,這個節點沒有任何子節點,但是它有一個父節點,需要通過返回null來將對應的父節點指針賦予null值(行{11})
現在節點的值已經是null了,父節點指向它的指針也會接收到這個值,這也是我們要在函數中返回節點的值的原因。父節點總是會接收到函數的返回值。另一種可行的辦法是將父節點和節點本身都作為參數傳入方法內部
如果回頭來看方法的第一行代碼,會發現我們在行{4}和行{7}更新了節點左右指針的值,同樣也在行{5}和行{8}返回了更新後的節點。下圖展現了移除一個葉節點的過程:
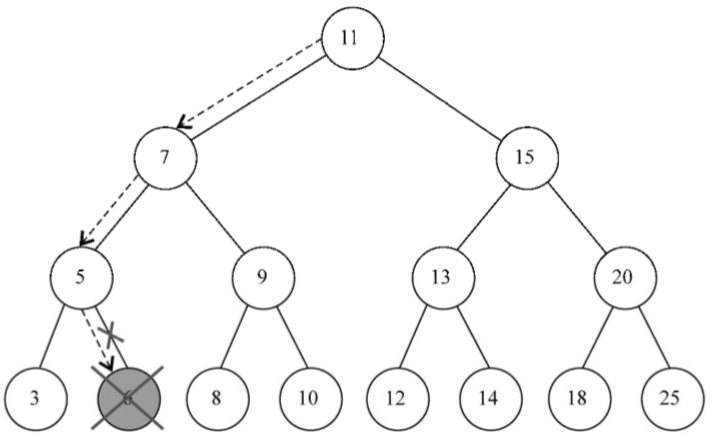
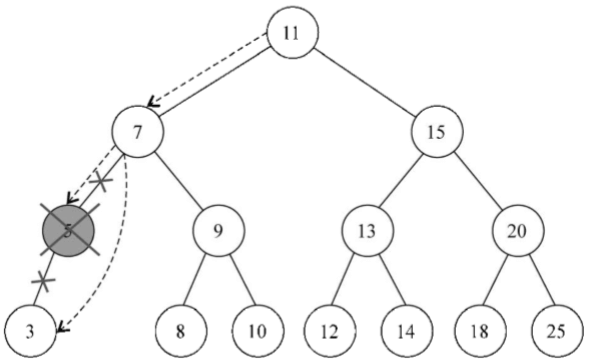
2、移除有一個左側或右側子節點的節點
現在來看第二種情況,移除有一個左側子節點或右側子節點的節點。這種情況下,需要跳過這個節點,直接將父節點指向它的指針指向子節點。如果這個節點沒有左側子節點(行{12}),也就是說它有一個右側子節點。因此我們把對它的引用改為對它右側子節點的引用(行{13})並返回更新後的節點(行{14})。如果這個節點沒有右側子節點,也是一樣——把對它的引用改為對它左側子節點的引用(行{16})並返回更新後的值(行{17})
下圖展現了移除只有一個左側子節點或右側子節點的節點的過程:
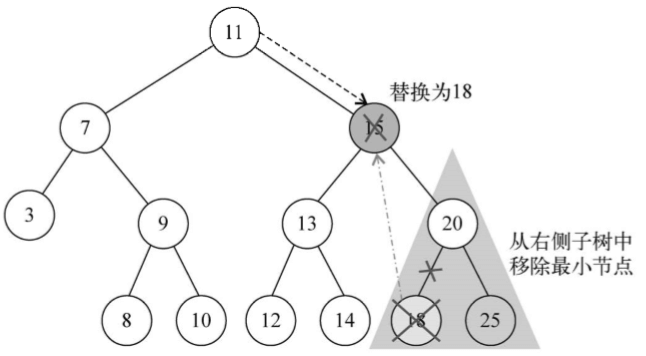
3、移除有兩個子節點的節點
現在是第三種情況,也是最複雜的情況,那就是要移除的節點有兩個子節點——左側子節點和右側子節點。要移除有兩個子節點的節點,需要執行四個步驟。(1)當找到了需要移除的節點後,需要找到它右邊子樹中最小的節點(它的繼承者——行{18});(2)然後,用它右側子樹中最小節點的鍵去更新這個節點的值(行{19})。通過這一步,改變了這個節點的鍵,也就是說它被移除了;(3)但是,這樣在樹中就有兩個擁有相同鍵的節點了,這是不行的。要繼續把右側子樹中的最小節點移除,畢竟它已經被移至要移除的節點的位置了(行{20});(4)最後,向它的父節點返回更新後節點的引用(行{21})
findMinNode方法的實現和min方法的實現方式是一樣的。唯一不同之處在於,在min方法中只返回鍵,而在findMinNode中返回了節點。下圖展現了移除有兩個子節點的節點的過程:
【完整代碼】
二叉搜索樹BST的完整代碼如下所示
function BinarySearchTree() { var Node = function(key){ this.key = key; this.left = null; this.right = null; }; var root = null; this.insert = function(key){ var newNode = new Node(key); //special case - first element if (root === null){ root = newNode; } else { insertNode(root,newNode); } }; var insertNode = function(node, newNode){ if (newNode.key < node.key){ if (node.left === null){ node.left = newNode; } else { insertNode(node.left, newNode); } } else { if (node.right === null){ node.right = newNode; } else { insertNode(node.right, newNode); } } }; this.getRoot = function(){ return root; }; this.search = function(key){ return searchNode(root, key); }; var searchNode = function(node, key){ if (node === null){ return false; } if (key < node.key){ return searchNode(node.left, key); } else if (key > node.key){ return searchNode(node.right, key); } else { //element is equal to node.item return true; } }; this.inOrderTraverse = function(callback){ inOrderTraverseNode(root, callback); }; var inOrderTraverseNode = function (node, callback) { if (node !== null) { inOrderTraverseNode(node.left, callback); callback(node.key); inOrderTraverseNode(node.right, callback); } }; this.preOrderTraverse = function(callback){ preOrderTraverseNode(root, callback); }; var preOrderTraverseNode = function (node, callback) { if (node !== null) { callback(node.key); preOrderTraverseNode(node.left, callback); preOrderTraverseNode(node.right, callback); } }; this.postOrderTraverse = function(callback){ postOrderTraverseNode(root, callback); }; var postOrderTraverseNode = function (node, callback) { if (node !== null) { postOrderTraverseNode(node.left, callback); postOrderTraverseNode(node.right, callback); callback(node.key); } }; this.min = function() { return minNode(root); }; var minNode = function (node) { if (node){ while (node && node.left !== null) { node = node.left; } return node.key; } return null; }; this.max = function() { return maxNode(root); }; var maxNode = function (node) { if (node){ while (node && node.right !== null) { node = node.right; } return node.key; } return null; }; this.remove = function(element){ root = removeNode(root, element); }; var findMinNode = function(node){ while (node && node.left !== null) { node = node.left; } return node; }; var removeNode = function(node, element){ if (node === null){ return null; } if (element < node.key){ node.left = removeNode(node.left, element); return node; } else if (element > node.key){ node.right = removeNode(node.right, element); return node; } else { //element is equal to node.item //handle 3 special conditions //1 - a leaf node //2 - a node with only 1 child //3 - a node with 2 children //case 1 if (node.left === null && node.right === null){ node = null; return node; } //case 2 if (node.left === null){ node = node.right; return node; } else if (node.right === null){ node = node.left; return node; } //case 3 var aux = findMinNode(node.right); node.key = aux.key; node.right = removeNode(node.right, aux.key); return node; } }; }
自平衡樹
二叉樹BST存在一個問題:取決於添加的節點數,樹的一條邊可能會非常深;也就是說,樹的一條分支會有很多層,而其他的分支卻只有幾層,如下圖所示:
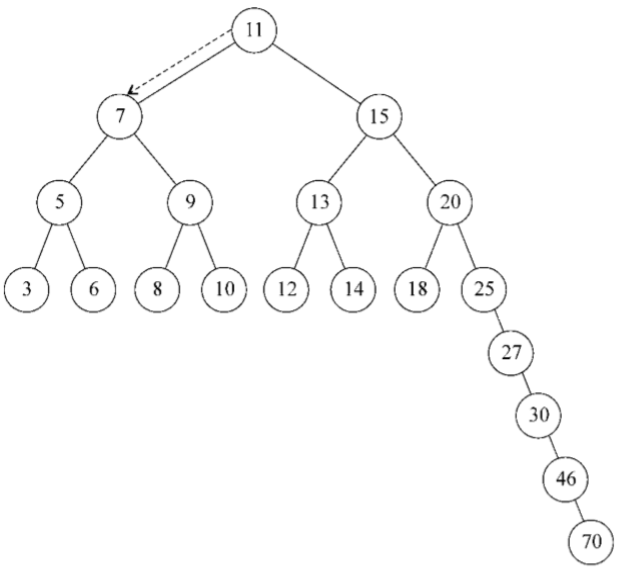
這會在需要在某條邊上添加、移除和搜索某個節點時引起一些性能問題。為瞭解決這個問題,有一種樹叫作阿德爾森-維爾斯和蘭迪斯樹(AVL樹)。AVL樹是一種自平衡二叉搜索樹,意思是任何一個節點左右兩側子樹的高度之差最多為1。也就是說這種樹會在添加或移除節點時儘量試著成為一棵完全樹
AVL樹是一種自平衡樹。添加或移除節點時,AVL樹會嘗試自平衡。任意一個節點(不論深度)的左子樹和右子樹高度最多相差1。添加或移除節點時,AVL樹會儘可能嘗試轉換為完全樹。
在AVL樹中插入或移除節點和BST完全相同。然而,AVL樹的不同之處在於我們需要檢驗它的平衡因數,如果有需要,則將其邏輯應用於樹的自平衡。
下麵的代碼是向AVL樹插入新節點的例子:
var insertNode = function(node, element) { if (node === null) { node = new Node(element); } else if (element < node.key) { node.left = insertNode(node.left, element); if (node.left !== null) { // 確認是否需要平衡 {1} } } else if (element > node.key) { node.right = insertNode(node.right, element); if (node.right !== null) { // 確認是否需要平衡 {2} } } return node; };
然而,插入新節點時,還要檢查是否需要平衡樹(行{1}和行{2})。
【計算平衡因數】
在AVL樹中,需要對每個節點計算右子樹高度(hr)和左子樹高度(hl)的差值,該值 (hr-hl)應為0、1或-1。如果結果不是這三個值之一,則需要平衡該AVL樹。這就是平衡因數的概念
下圖舉例說明瞭一些樹的平衡因數(所有的樹都是平衡的):
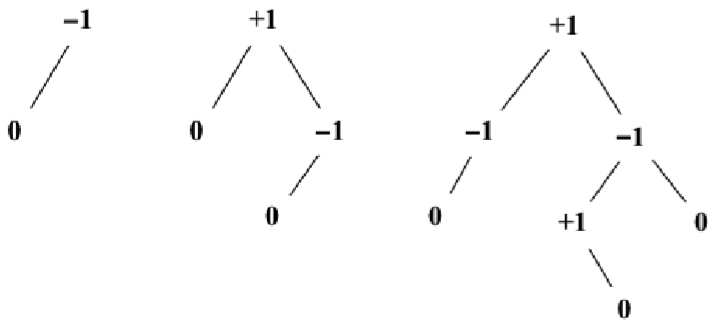
計算節點高度的代碼如下:
var heightNode = function(node) { if (node === null) { return -1; } else { return Math.max(heightNode(node.left), heightNode(node.right)) + 1; } };
因此,向左子樹插入新節點時,需要計算其高度;如果高度大於1(即不為-1、0和1之一), 就需要平衡左子樹。代碼如下:
// 替換insertNode方法的行{1} if ((heightNode(node.left) - heightNode(node.right)) > 1) { // 旋轉 {3} }
向右子樹插入新節點時,應用同樣的邏輯,代碼如下:
// 替換insertNode方法的行{2} if ((heightNode(node.right) - heightNode(node.left)) > 1) { // 旋轉 {4} }
【AVL旋轉】
向AVL樹插入節點時,可以執行單旋轉或雙旋轉兩種平衡操作,分別對應四種場景:
1、右-右(RR):向左的單旋轉 2、左-左(LL):向右的單旋轉 3、左-右(LR):向右的雙旋轉 4、右-左(RL):向左的雙旋轉
下麵來依次看看它們是如何工作的
右-右(RR):向左的單旋轉。如下圖所示:
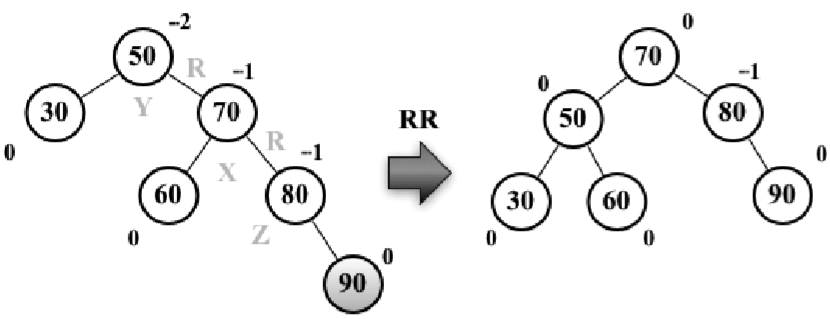
假設向AVL樹插入節點90,這會造成樹失衡(節點50 -Y高度為+2),因此需要恢復樹的平衡。下麵是執行的操作:
1、與平衡操作相關的節點有三個(X、Y、Z),將節點X置於節點Y(平衡因數為-2)所在的位置(行{1})
2、節點X的右子樹保持不變
3、將節點Y的右子節點置為節點X的左子節點Z(行{2})
4、將節點X的左子節點置為節點Y(行{3})
下麵的代碼舉例說明瞭整個過程:
var rotationRR = function(node) { var tmp = node.right; // {1} node.right = tmp.left; // {2} tmp.left = node; // {3} return tmp; };
左-左(LL):向右的單旋轉。如下圖所示:
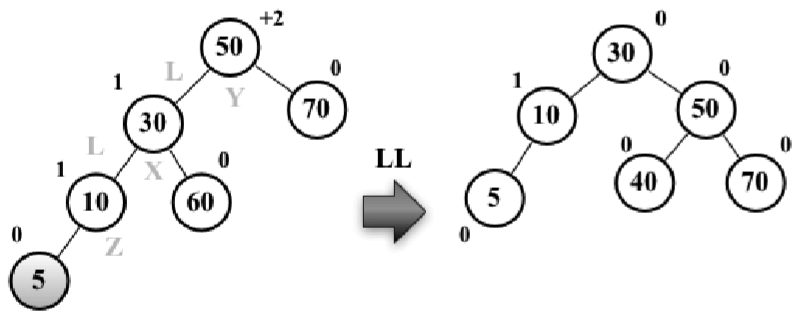
假設向AVL樹插入節點5,這會造成樹失衡(節點50 -Y高度為+2),需要恢復樹的平衡。下麵是我們執行的操作:
1、與平衡操作相關的節點有三個(X、Y、Z),將節點X置於節點Y(平衡因數為+2)所在的位置(行{1})
2、節點X的左子樹保持不變
3、將節點Y的左子節點置為節點X的右子節點Z(行{2})
4、將節點X的右子節點置為節點Y(行{3})
下麵的代碼舉例說明瞭整個過程:
var rotationLL = function(node) { var tmp = node.left; // {1} node.left = tmp.right; // {2} tmp.right = node; // {3} return tmp; };
左-右(LR):向右的雙旋轉。如下圖所示:
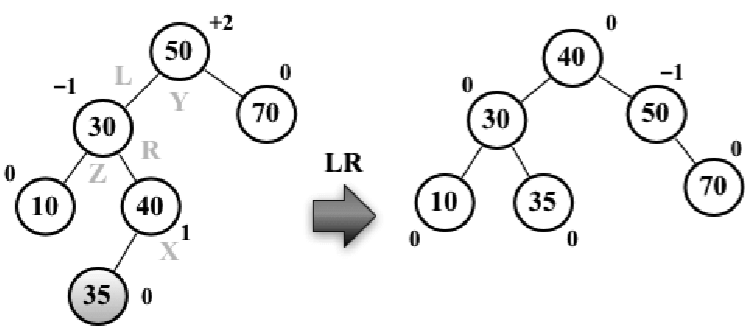
假設向AVL樹插入節點35,這會造成樹失衡(節點50 -Y高度為+2),需要恢復樹的平衡。下麵是執行的操作:
1、將節點X置於節點Y(平衡因數為+2)所在的位置
2、將節點Y的左子節點置為節點X的右子節點
3、將節點Z的右子節點置為節點X的左子節點
4、將節點X的右子節點置為節點Y
5、將節點X的左子節點置為節點Z
基本上,就是先做一次RR旋轉,再做一次LL旋轉。下麵的代碼舉例說明瞭整個過程:
var rotationLR = function(node) { node.left = rotationRR(node.left); return rotationLL(node); };
右-左(RL):向左的雙旋轉。如下圖所示:
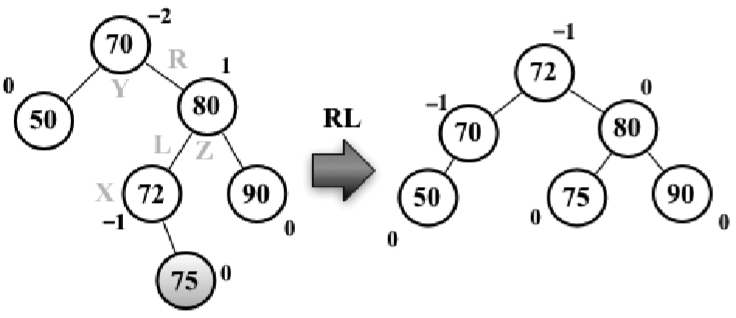
假設向AVL樹插入節點75,這會造成樹失衡(節點70 -Y高度為-2),需要恢復樹的平衡。下麵是我們執行的操作:
1、將節點X置於節點Y(平衡因數為-2)所在的位置
2、節點Z的左子節點置為節點X的右子節點
3、將節點Y的右子節點置為節點X的左子節點
4、將節點X的左子節點置為節點Y
5、將節點X的右子節點置為節點Z
基本上,就是先做一次LL旋轉,再做一次RR旋轉。下麵的代碼舉例說明瞭整個過程:
var rotationRL = function(node) { node.right = rotationLL(node.right); return rotationRR(node); };
確認樹需要平衡後,就需要對每種情況分別應用正確的旋轉
向左子樹插入新節點,且節點的值小於其左子節點時,應進行LL旋轉。否則,進行LR旋轉。該過程的代碼如下:
// 替換insertNode方法的行{1} if ((heightNode(node.left) - heightNode(node.right)) > 1){ // 旋轉 {3} if (element <


