前端學數據結構之圖

来源:https://www.cnblogs.com/xiaohuochai/archive/2018/01/04/8185671.html
-Advertisement-
Play Games

[1]數據結構 [2]圖的表示 [3]創建Graph類 [4]圖的遍歷 [5]最短路徑演算法 [6]最小生成樹 ...


前面的話

　　本文將詳細介紹圖這種數據結構，包含不少圖的巧妙運用

 

數據結構

　　圖是網路結構的抽象模型。圖是一組由邊連接的節點（或頂點）。圖是重要的，因為任何二元關係都可以用圖來表示

　　任何社交網路，例如Facebook、Twitter和Google plus，都可以用圖來表示。還可以使用圖來表示道路、航班以及通信狀態，如下圖所示：

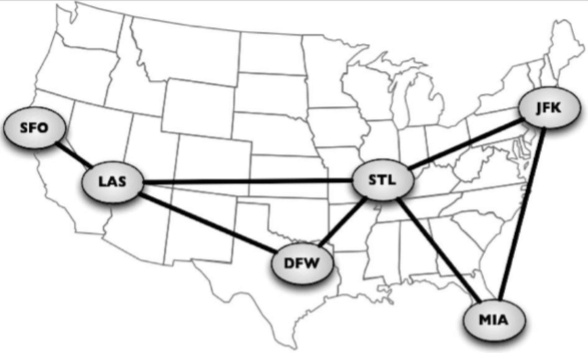
graph1

　　一個圖G = (V, E)由以下元素組成

V：一組頂點
E：一組邊，連接V中的頂點

　　下圖表示一個圖：

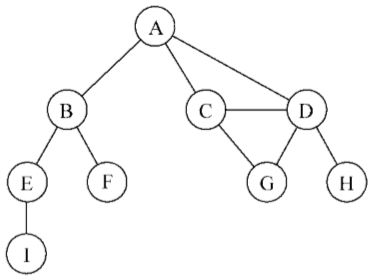
graph2

　　在著手實現演算法之前，先瞭解一下圖的一些術語

　　由一條邊連接在一起的頂點稱為相鄰頂點。比如，A和B是相鄰的，A和D是相鄰的，A和C是相鄰的，A和E不是相鄰的。

　　一個頂點的度是其相鄰頂點的數量。比如，A和其他三個頂點相連接，因此，A的度為3；E和其他兩個頂點相連，因此，E的度為2。

　　路徑是頂點v1,v2,…,vk的一個連續序列，其中vi和vi+1是相鄰的。以上一示意圖中的圖為例，其中包含路徑A B E I和A C D G。

　　簡單路徑要求不包含重覆的頂點。舉個例子，ADG是一條簡單路徑。除去最後一個頂點（因為它和第一個頂點是同一個頂點），環也是一個簡單路徑，比如ADCA（最後一個頂點重新回到A）

　　如果圖中不存在環，則稱該圖是無環的。如果圖中每兩個頂點間都存在路徑，則該圖是連通的

【有向圖和無向圖】

　　圖可以是無向的（邊沒有方向）或是有向的（有向圖）。如下圖所示，有向圖的邊有一個方向：

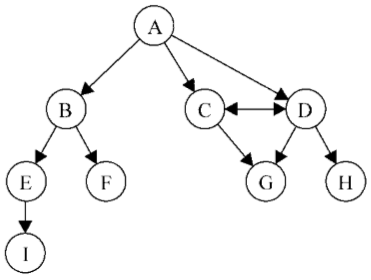
graph3

　　如果圖中每兩個頂點間在雙向上都存在路徑，則該圖是強連通的。例如，C和D是強連通的，而A和B不是強連通的。

　　圖還可以是未加權的（目前為止我們看到的圖都是未加權的）或是加權的。如下圖所示，加權圖的邊被賦予了權值：

graph4

　　可以使用圖來解決電腦科學世界中的很多問題，比如搜索圖中的一個特定頂點或搜索一條特定邊，尋找圖中的一條路徑（從一個頂點到另一個頂點），尋找兩個頂點之間的最短路徑，以及環檢測

 

圖的表示

　　從數據結構的角度來說，有多種方式來表示圖。在所有的表示法中，不存在絕對正確的方式。圖的正確表示法取決於待解決的問題和圖的類型

【鄰接矩陣】

　　圖最常見的實現是鄰接矩陣。每個節點都和一個整數相關聯，該整數將作為數組的索引。我 們用一個二維數組來表示頂點之間的連接。如果索引為i的節點和索引為j的節點相鄰，則array[i][j] === 1，否則array[i][j] === 0，如下圖所示：

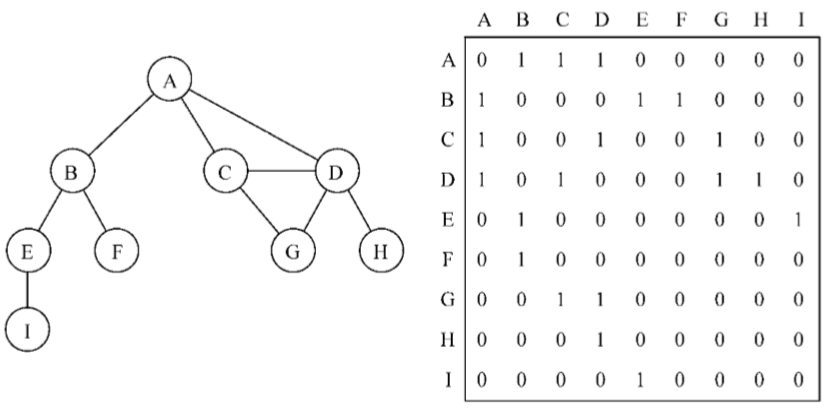
graph5

　　不是強連通的圖（稀疏圖）如果用鄰接矩陣來表示，則矩陣中將會有很多0，這意味著我們浪費了電腦存儲空間來表示根本不存在的邊。例如，找給定頂點的相鄰頂點，即使該頂點只有一個相鄰頂點，我們也不得不迭代一整行。鄰接矩陣表示法不夠好的另一個理由是，圖中頂點的數量可能會改變，而2維數組不太靈活

【鄰接表】

　　也可以使用一種叫作鄰接表的動態數據結構來表示圖。鄰接表由圖中每個頂點的相鄰頂點列表所組成。存在好幾種方式來表示這種數據結構。我們可以用列表（數組）、鏈表，甚至是散列表或是字典來表示相鄰頂點列表。下麵的示意圖展示了鄰接表數據結構

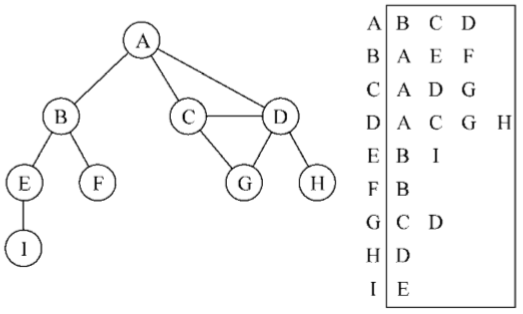
graph6

　　儘管鄰接表可能對大多數問題來說都是更好的選擇，但以上兩種表示法都很有用，且它們有著不同的性質（例如，要找出頂點v和w是否相鄰，使用鄰接矩陣會比較快）

【關聯矩陣】

　　還可以用關聯矩陣來表示圖。在關聯矩陣中，矩陣的行表示頂點，列表示邊。如下圖所示，使用二維數組來表示兩者之間的連通性，如果頂點v是邊e的入射點，則array[v][e] === 1； 否則，array[v][e] === 0

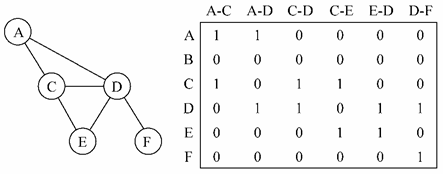
graph7

　　關聯矩陣通常用於邊的數量比頂點多的情況下，以節省空間和記憶體

 

創建Graph類

　　聲明類的骨架：

function Graph() {
  var vertices = []; //{1}
  var adjList = new Dictionary(); //{2}
}

　　使用一個數組來存儲圖中所有頂點的名字（行{1}），以及一個字典來存儲鄰接表（行{2}）。字典將會使用頂點的名字作為鍵，鄰接頂點列表作為值。vertices數組和adjList字典兩者都是我們Graph類的私有屬性

　　接著，將實現兩個方法：一個用來向圖中添加一個新的頂點（因為圖實例化後是空的），另外一個方法用來添加頂點之間的邊

　　先實現addVertex方法：

this.addVertex = function(v){ 
  vertices.push(v); //{3} 
  adjList.set(v, []); //{4}
};

　　這個方法接受頂點v作為參數。將該頂點添加到頂點列表中（行{3}），並且在鄰接表中，設置頂點v作為鍵對應的字典值為一個空數組（行{4}）

　　現在，來實現addEdge方法：

this.addEdge = function(v, w){ 
  adjList.get(v).push(w); //{5}
  adjList.get(w).push(v); //{6}
};

　　這個方法接受兩個頂點作為參數。首先，通過將w加入到v的鄰接表中，添加了一條自頂點v到頂點w的邊。如果想實現一個有向圖，則行{5}就足夠了。如果是基於無向圖的，需要添加一條自w向v的邊（行{6}）

　　下麵來測試這段代碼：

var graph = new Graph();
var myVertices = ['A','B','C','D','E','F','G','H','I']; //{7}
for (var i=0; i<myVertices.length; i++){ //{8} 
  graph.addVertex(myVertices[i]);
}
graph.addEdge('A', 'B'); //{9}
graph.addEdge('A', 'C');
graph.addEdge('A', 'D');
graph.addEdge('C', 'D');
graph.addEdge('C', 'G');
graph.addEdge('D', 'G');
graph.addEdge('D', 'H');
graph.addEdge('B', 'E');
graph.addEdge('B', 'F');
graph.addEdge('E', 'I');

　　為方便起見，創建了一個數組，包含所有想添加到圖中的頂點（行{7}）。接下來，只要遍歷vertices數組並將其中的值逐一添加到我們的圖中（行{8}）。最後，添加想要的邊（行{9}）。這段代碼將會創建一個圖，也就是到前面的示意圖所使用的

　　為了更方便一些，下麵來實現一下Graph類的toString方法，以便於在控制台輸出圖

this.toString = function(){ 
  var s = '';
  for (var i=0; i<vertices.length; i++){ //{10} 
    s += vertices[i] + ' -> ';
    var neighbors = adjList.get(vertices[i]); //{11} 
    for (var j=0; j<neighbors.length; j++){ //{12}
      s += neighbors[j] + ' ';
    }
    s += '\n'; //{13}
  }
  return s;
};

　　我們為鄰接表表示法構建了一個字元串。首先，迭代vertices數組列表（行{10}），將頂點的名字加入字元串中。接著，取得該頂點的鄰接表（行{11}），同樣也迭代該鄰接表（行{12}），將相鄰頂點加入我們的字元串。鄰接表迭代完成後，給我們的字元串添加一個換行符（行{13}），這樣就可以在控制台看到一個漂亮的輸出了。運行如下代碼：

console.log(graph.toString());

　　輸出如下：

A -> B C D 
B -> A E F 
C -> A D G
D -> A C G H 
E -> B I
F -> B
G -> C D 
H -> D
I -> E

　　從該輸出中，頂點A有這幾個相鄰頂點：B、C和D

 

圖的遍歷

　　和樹數據結構類似，可以訪問圖的所有節點。有兩種演算法可以對圖進行遍歷：廣度優先搜索（Breadth-First Search，BFS）和深度優先搜索（Depth-First Search，DFS）。圖遍歷可以用來尋找特定的頂點或尋找兩個頂點之間的路徑，檢查圖是否連通，檢查圖是否含有環等

　　在實現演算法之前，需要理解圖遍歷的思想方法。圖遍歷演算法的思想是必須追蹤每個第一次訪問的節點，並且追蹤有哪些節點還沒有被完全探索。對於兩種圖遍歷演算法，都需要明確指出第一個被訪問的頂點

　　完全探索一個頂點要求我們查看該頂點的每一條邊。對於每一條邊所連接的沒有被訪問過的頂點，將其標註為被髮現的，並將其加進待訪問頂點列表中

　　為了保證演算法的效率，務必訪問每個頂點至多兩次。連通圖中每條邊和頂點都會被訪問到

　　廣度優先搜索演算法和深度優先搜索演算法基本上是相同的，只有一點不同，那就是待訪問頂點列表的數據結構

演算法           數據結構    描    述
深度優先搜索    棧         通過將頂點存入棧中，頂點是沿著路徑被探索的，存在新的相鄰頂點就去訪問
廣度優先搜索    隊列      通過將頂點存入隊列中，最先入隊列的頂點先被探索

　　當要標註已經訪問過的頂點時，用三種顏色來反映它們的狀態

白色：表示該頂點還沒有被訪問。
灰色：表示該頂點被訪問過，但並未被探索過。
黑色：表示該頂點被訪問過且被完全探索過。

　　這就是之前提到的務必訪問每個頂點最多兩次的原因

【廣度優先搜索】

　　廣度優先搜索演算法會從指定的第一個頂點開始遍歷圖，先訪問其所有的相鄰點，就像一次訪問圖的一層。換句話說，就是先寬後深地訪問頂點，如下圖所示：

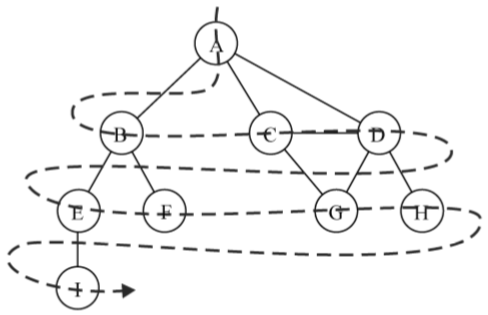
graph8

　　以下是從頂點v開始的廣度優先搜索演算法所遵循的步驟

　　(1) 創建一個隊列Q。
　　(2) 將v標註為被髮現的（灰色），並將v入隊列Q。
　　(3) 如果Q非空，則運行以下步驟：
　　　　(a) 將u從Q中出隊列；
　　　　(b) 將標註u為被髮現的（灰色）；
　　　　(c) 將u所有未被訪問過的鄰點（白色）入隊列；
　　　　(d) 將u標註為已被探索的（黑色）

　　下麵來實現廣度優先搜索演算法：

var initializeColor = function(){ 
  var color = [];
  for (var i=0; i<vertices.length; i++){
    color[vertices[i]] = 'white'; //{1}
  }
  return color;
};
this.bfs = function(v, callback){
  var color = initializeColor(), //{2} 
  queue = new Queue();    //{3} 
  queue.enqueue(v);        //{4}
  while (!queue.isEmpty()){    //{5} 
    var u = queue.dequeue(),    //{6}
    neighbors = adjList.get(u); //{7}
    color[u] = 'grey';    // {8} 
    for (var i=0; i<neighbors.length; i++){ // {9}
      var w = neighbors[i];    // {10}
      if (color[w] === 'white'){    // {11}
        color[w] = 'grey';    // {12}
        queue.enqueue(w);    // {13}
      }
    }
    color[u] = 'black'; // {14} 
    if (callback) {    // {15}
      callback(u);
    }
  }
};

　　廣度優先搜索和深度優先搜索都需要標註被訪問過的頂點。為此，將使用一個輔助數組color。由於當演算法開始執行時，所有的頂點顏色都是白色（行{1}），所以可以創建一個輔助函數initializeColor，為這兩個演算法執行此初始化操作

　　下麵來深入廣度優先搜索方法的實現。要做的第一件事情是用initializeColor函數來將color數組初始化為white（行{2}）。還需要聲明和創建一個Queue實例（行{3}），它將會存儲待訪問和待探索的頂點。bfs方法接受一個頂點作為演算法的起始點。起始頂點是必要的，將此頂點入隊列（行{4}）。如果隊列非空（行{5}），將通過出隊列（行{6}）操作從隊列中移除一個頂點，並取得一個包含其所有鄰點的鄰接表（行{7}）。該頂點將被標註為grey（行{8}），表示發現了它（但還未完成對其的探索）。

　　對於u（行{9}）的每個鄰點，取得其值（該頂點的名字——行{10}），如果它還未被訪問過（顏色為white——行{11}），則將其標註為已經發現了它（顏色設置為grey——行{12}），並將這個頂點加入隊列中（行{13}），這樣當其從隊列中出列的時候，可以完成對其的探索。當完成探索該頂點 和其相鄰頂點後，將該頂點標註為已探索過的（顏色設置為black——行{14}）

　　實現的這個bfs方法也接受一個回調。這個參數是可選的，如果傳遞了回調函數（行{15}），會用到它。執行下麵這段代碼來測試一下這個演算法：

function printNode(value){ //{16} 
  console.log('Visited vertex: ' + value); //{17}
}
graph.bfs(myVertices[0], printNode); //{18}

　　首先，聲明瞭一個回調函數（行{16}），它僅僅在瀏覽器控制臺上輸出已經被完全探索過的頂點的名字。接著，調用bfs方法，給它傳遞第一個頂點（A——myVertices數組）和回調函數。執行這段代碼時，該演算法會在瀏覽器控制台輸出下示的結果：

Visited vertex: A 
Visited vertex: B 
Visited vertex: C 
Visited vertex: D 
Visited vertex: E 
Visited vertex: F 
Visited vertex: G 
Visited vertex: H 
Visited vertex: I

　　頂點被訪問的順序和示意圖中所展示的一致

　　考慮如何來解決下麵這個問題。給定一個圖G和源頂點v，找出對每個頂點u，u和v之間最短路徑的距離（以邊的數量計）。 對於給定頂點v，廣度優先演算法會訪問所有與其距離為1的頂點，接著是距離為2的頂點，以此類推。所以，可以用廣度優先演算法來解這個問題。可以修改bfs方法以返回給我們一些信息：

從v到u的距離d[u]；
前溯點pred[u]，用來推導出從v到其他每個頂點u的最短路徑。

　　下麵是改進過的廣度優先方法的實現：

this.BFS = function(v){
  var color = initializeColor(), 
      queue = new Queue(),
      d = [],    //{1}
      pred = []; //{2}
      queue.enqueue(v);
  for (var i=0; i<vertices.length; i++){ //{3} 
    d[vertices[i]] = 0;    //{4}
    pred[vertices[i]] = null;    //{5}
  }
  while (!queue.isEmpty()){ 
    var u = queue.dequeue(),
    neighbors = adjList.get(u);
    color[u] = 'grey';
    for (i=0; i<neighbors.length; i++){ 
      var w = neighbors[i];
      if (color[w] === 'white'){
        color[w] = 'grey';
        d[w] = d[u] + 1;    //{6}
        pred[w] = u;    //{7}
        queue.enqueue(w);
      }
    }
  color[u] = 'black';
  }
  return { //{8} 
    distances: d, 
    predecessors: pred
  };
};

　　還需要聲明數組d（行{1}）來表示距離，以及pred數組來表示前溯點。下一步則是對圖中的每一個頂點，用0來初始化數組d（行{4}），用null來初始化數組pred。發現頂點u的鄰點w時，則設置w的前溯點值為u（行{7}）。還通過給d[u]加1來設置v和w之間的距離（u是w的前溯點，d[u]的值已經有了）。方法最後返回了一個包含d和pred的對象（行{8}）

　　現在，可以再次執行BFS方法，並將其返回值存在一個變數中：

var shortestPathA = graph.BFS(myVertices[0]); 
console.log(shortestPathA);

　　對頂點A執行BFS方法，以下將會是輸出：

distances: [A: 0, B: 1, C: 1, D: 1, E: 2, F: 2, G: 2, H: 2 , I: 3],
predecessors: [A: null, B: "A", C: "A", D: "A", E: "B", F: "B", G:"C", H: "D", I: "E"]

　　這意味著頂點A與頂點B、C和D的距離為1；與頂點E、F、G和H的距離為2；與頂點I的距離為3。通過前溯點數組，可以用下麵這段代碼來構建從頂點A到其他頂點的路徑：

var fromVertex = myVertices[0]; //{9}
for (var i=1; i<myVertices.length; i++){ //{10} 
  var toVertex = myVertices[i], //{11}
  path = new Stack();    //{12} 
  for (var v=toVertex; v!== fromVertex; v=shortestPathA.predecessors[v]) { //{13} 
    path.push(v);    //{14}
  }
  path.push(fromVertex);    //{15}
  var s = path.pop();    //{16} 
  while (!path.isEmpty()){    //{17}
    s += ' - ' + path.pop(); //{18}
  }
  console.log(s); //{19}
}

　　用頂點A作為源頂點（行{9}）。對於每個其他頂點（除了頂點A——行{10}），會計算頂點A到它的路徑。從頂點數組得到toVertex（行{11}），然後會創建一個棧來存儲路徑值（行{12}）。接著，追溯toVertex到fromVertex的路徑{行{13}}。變數v被賦值為其前溯點的值，這樣能夠反向追溯這條路徑。將變數v添加到棧中（行{14}）。最後，源頂點也會被添加到棧中，以得到完整路徑。

　　這之後，創建了一個s字元串，並將源頂點賦值給它（它是最後一個加入棧中的，所以它是第一個被彈出的項 ——行{16}）。當棧是非空的，就從棧中移出一個項並將其拼接到字元串s的後面（行{18}）。最後（行{19}）在控制臺上輸出路徑。執行該代碼段，會得到如下輸出：

A - B
A - C
A - D
A - B - E
A - B - F
A - C - G
A - D - H
A    - B - E - I

　　這裡，得到了從頂點A到圖中其他頂點的最短路徑（衡量標準是邊的數量）

　　如果要計算加權圖中的最短路徑（例如，城市A和城市B之間的最 短路徑——GPS和Google Maps中用到的演算法），廣度優先搜索未必合適。

　　舉些例子，Dijkstra’s演算法解決了單源最短路徑問題。Bellman–Ford演算法解決了邊權值為負的單源最短路徑問題。A*搜索演算法解決了求僅一對頂點間的最短路徑問題，它用經驗法則來加速搜索過程。Floyd–Warshall演算法解決了求所有頂點對間的最短路徑這一問題。

　　圖是一個廣泛的主題，對最短路徑問題及其變種問題，有很多的解決方案。但在開始學習這些其他解決方案前，需要掌握好圖的基本概念

【深度優先搜索】

 　　深度優先搜索演算法將會從第一個指定的頂點開始遍歷圖，沿著路徑直到這條路徑最後一個頂點被訪問了，接著原路回退並探索下一條路徑。換句話說，它是先深度後廣度地訪問頂點，如下圖所示：

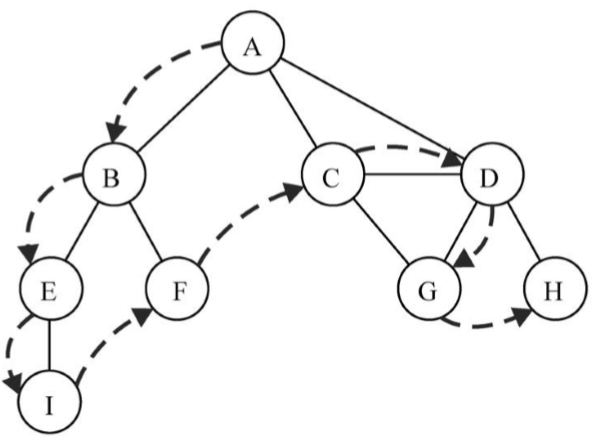
graph9

　　深度優先搜索演算法不需要一個源頂點。在深度優先搜索演算法中，若圖中頂點v未訪問，則訪問該頂點v。要訪問頂點v，照如下步驟做

　　1、標註v為被髮現的（灰色）。

　　2、對於v的所有未訪問的鄰點w，訪問頂點w，標註v為已被探索的（黑色）

　　深度優先搜索的步驟是遞歸的，這意味著深度優先搜索演算法使用棧來存儲函數調用（由遞歸調用所創建的棧）

　　下麵來實現一下深度優先演算法：

this.dfs = function(callback){
  var color = initializeColor(); //{1}
  for (var i=0; i<vertices.length; i++){ //{2} 
    if (color[vertices[i]] === 'white'){ //{3}
      dfsVisit(vertices[i], color, callback); //{4}
    }
  }
};
var dfsVisit = function(u, color, callback){ 
  color[u] = 'grey'; //{5}
  if (callback) {    //{6}
    callback(u);
  }
  var neighbors = adjList.get(u);        //{7} 
  for (var i=0; i<neighbors.length; i++){ //{8} 
    var w = neighbors[i];    //{9}
    if (color[w] === 'white'){    //{10}
      dfsVisit(w, color, callback);    //{11}
    }
  }
  color[u] = 'black'; //{12}
};

　　首先，創建顏色數組（行{1}），並用值white為圖中的每個頂點對其做初始化，廣度優先搜索也這麼做的。接著，對於圖實例中每一個未被訪問過的頂點（行{2}和{3}），調用私有的遞歸函數dfsVisit，傳遞的參數為頂點、顏色數組以及回調函數（行{4}）

　　當訪問u頂點時，標註其為被髮現的（grey——行{5}）。如果有callback函數的話（行{6}），則執行該函數輸出已訪問過的頂點。接下來一步是取得包含頂點u所有鄰點的列表（行{7}）。對於頂點u的每一個未被訪問過（顏色為white——行{10}和行{8}）的鄰點w（行{9}）， 將調用dfsVisit函數，傳遞w和其他參數（行{11}——添加頂點w入棧，這樣接下來就能訪問它）。最後，在該頂點和鄰點按深度訪問之後，我們回退，意思是該頂點已被完全探索，並將其標註為black（行{12}）

　　執行下麵的代碼段來測試一下dfs方法：

graph.dfs(printNode);

　　輸出如下：

Visited vertex: A 
Visited vertex: B 
Visited vertex: E 
Visited vertex: I 
Visited vertex: F 
Visited vertex: C
Visited vertex: D 
Visited vertex: G 
Visited vertex: H

　　這個順序和示意圖所展示的一致。下麵這個示意圖展示了該演算法每一步的執行過程：

graph10

　　行{4}只會被執行一次，因為所有其他的頂點都有路徑到第一個調用dfsVisit函數的頂點（頂點A）。如果頂點B第一個調用函數，則行{4}將會為其他頂點再執行一次（比如頂點A）

　　到目前為止，只是展示了深度優先搜索演算法的工作原理。可以用該演算法做更多的事情，而不只是輸出被訪問頂點的順序

　　對於給定的圖G，希望深度優先搜索演算法遍歷圖G的所有節點，構建“森林”（有根樹的一個集合）以及一組源頂點（根），並輸出兩個數組：發現時間和完成探索時間。可以修改dfs方法來返回一些信息：

頂點u的發現時間d[u]；
當頂點u被標註為黑色時，u的完成探索時間f[u]；
頂點u的前溯點p[u]。

　　來看看改進了的DFS方法的實現：

var time = 0; //{1} 
this.DFS = function(){
  var color = initializeColor(), //{2}
      d = [],
      f = [],
      p = [];
      time = 0;
  for (var i=0; i<vertices.length; i++){ //{3}
    f[vertices[i]] = 0;
    d[vertices[i]] = 0; 
    p[vertices[i]] = null;
  }
  for (i=0; i<vertices.length; i++){
    if (color[vertices[i]] === 'white'){ 
      DFSVisit(vertices[i], color, d, f, p);
    }
  }
  return {    //{4} 
    discovery: d, 
    finished: f, 
    predecessors: p
  };
};
var DFSVisit = function(u, color, d, f, p){ 
  console.log('discovered ' + u); 
  color[u] = 'grey';
  d[u] = ++time; //{5}
  var neighbors = adjList.get(u);
  for (var i=0; i<neighbors.length; i++){ 
    var w = neighbors[i];
    if (color[w] === 'white'){
      p[w] = u;    // {6}
      DFSVisit(w,color, d, f, p);
    }
  }
  color[u] = 'black';
  f[u] = ++time;    //{7}
  console.log('explored ' + u);
};

　　需要一個變數來要追蹤發現時間和完成探索時間（行{1}）。時間變數不能被作為參數傳遞，因為非對象的變數不能作為引用傳遞給其他JavaScript方法（將變數作為引用傳遞的意思是如果該變數在其他方法內部被修改，新值會在原始變數中反映出來）。接下來，聲明數組d、f和p（行{2}）。需要為圖的每一個頂點來初始化這些數組（行{3}）。在這個方法結尾處返回這些值（行{4}），之後要用到它們

　　當一個頂點第一次被髮現時，追蹤其發現時間（行{5}）。當它是由引自頂點u的邊而被髮現的，追蹤它的前溯點（行{6}）。最後，當這個頂點被完全探索後，追蹤其完成時間（行{7}）

　　深度優先演算法背後的思想是什麼？邊是從最近發現的頂點u處被向外探索的。只有連接到未發現的頂點的邊被探索了。當u所有的邊都被探索了，該演算法回退到u被髮現的地方去探索其他的邊。這個過程持續到發現了所有從原始頂點能夠觸及的頂點。如果還留有任何其他未被髮現的頂點，對新源頂點重覆這個過程。重覆該演算法，直到圖中所有的頂點都被探索了

　　對於改進過的深度優先搜索，有兩點需要註意

　　1、時間（time）變數值的範圍只可能在圖頂點數量的一倍到兩倍之間

　　2、對於所有的頂點u，d[u]<f[u]（意味著，發現時間的值比完成時間的值小，完成時間意思是所有頂點都已經被探索過了）

　　在這兩個假設下，有如下的規則：

1≤d[u]<f[u]≤2|V|

　　如果對同一個圖再跑一遍新的深度優先搜索方法，對圖中每個頂點，會得到如下的發現

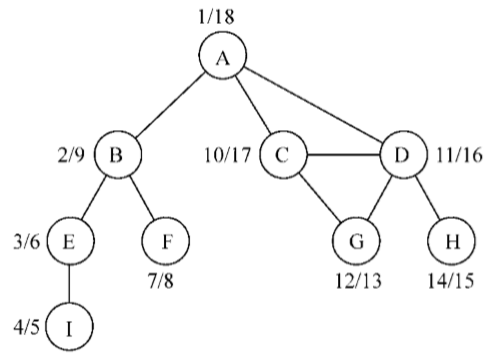
graph11

　　給定下圖，假定每個頂點都是一個需要去執行的任務：

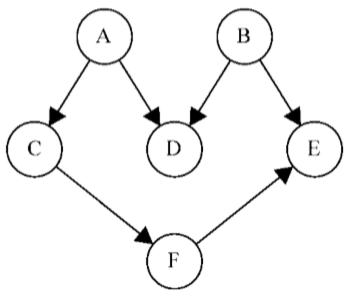
graph12

　　這是一個有向圖，意味著任務的執行是有順序的。例如，任務F不能在任務A之前執行。這個圖沒有環，意味著這是一個無環圖。所以，可以說該圖是一個有向無環圖（DAG）

　　當需要編排一些任務或步驟的執行順序時，這稱為拓撲排序（topologicalsorting，英文亦寫作topsort或是toposort）。在日常生活中，這個問題在不同情形下都會出現。例如，開始學習一門電腦科學課程，在學習某些知識之前得按順序完成一些知識儲備（不可以在上演算法I前先上演算法II）。在開發一個項目時，需要按順序執行一些步驟，例如，首先得從客戶那裡得到需求，接著開發客戶要求的東西，最後交付項目。不能先交付項目再去收集需求

　　拓撲排序只能應用於DAG。那麼，如何使用深度優先搜索來實現拓撲排序呢？在前面的示意圖上執行一下深度優先搜索

graph = new Graph();
myVertices = ['A','B','C','D','E','F'];
for(i=0;i<myVertices.length;i++){
  graph.addVertex(myVertices[i]);
}
graph.addEdge('A','C');
graph.addEdge('A','D');
graph.addEdge('B','D');
graph.addEdge('B','E');
graph.addEdge('C','F');
graph.addEdge('F','E');
var result = graph.DFS();

　　這段代碼將創建圖，添加邊，執行改進版本的深度優先搜索演算法，並將結果保存到result變數。下圖展示了深度優先搜索演算法執行後，該圖的發現和完成時間

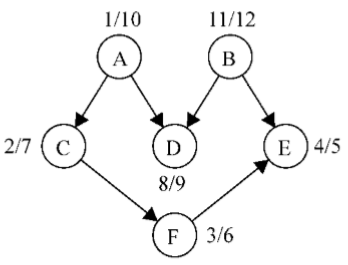
graph13

　　現在要做的僅僅是以倒序來排序完成時間數組，這便得出了該圖的拓撲排序：

B - A - D - C - F - E

　　註意之前的拓撲排序結果僅是多種可能性之一。如果稍微修改一下演算法，就會有不同的結果，比如下麵這個結果也是眾多其他可能性中的一個：

A - B - C - D - F - E

　　這也是一個可以接受的結果

【完整代碼】

　　Graph類的完整代碼如下所示

function Graph() {

    var vertices = []; //list

    var adjList = new Dictionary();

    this.addVertex = function(v){
        vertices.push(v);
        adjList.set(v, []); //initialize adjacency list with array as well;
    };

    this.addEdge = function(v, w){
        adjList.get(v).push(w);
        //adjList.get(w).push(v); //commented to run the improved DFS with topological sorting
    };

    this.toString = function(){
        var s = '';
        for (var i=0; i<vertices.length; i++){
            s += vertices[i] + ' -> ';
            var neighbors = adjList.get(vertices[i]);
            for (var j=0; j<neighbors.length; j++){
                s += neighbors[j] + ' ';
            }
            s += '\n';
        }
        return s;
    };

    var initializeColor = function(){
        var color = {};
        for (var i=0; i<vertices.length; i++){
            color[vertices[i]] = 'white';
        }
        return color;
    };

    this.bfs = function(v, callback){

        var color = initializeColor(),
            queue = new Queue();
        queue.enqueue(v);

        while (!queue.isEmpty()){
            var u = queue.dequeue(),
                neighbors = adjList.get(u);
            color[u] = 'grey';
            for (var i=0; i<neighbors.length; i++){
                var w = neighbors[i];
                if (color[w] === 'white'){
                    color[w] = 'grey';
                    queue.enqueue(w);
                }
            }
            color[u] = 'black';
            if (callback) {
                callback(u);
            }
        }
    };

    this.dfs = function(callback){

        var color = initializeColor();

        for (var i=0; i<vertices.length; i++){
            if (color[vertices[i]] === 'white'){
                dfsVisit(vertices[i], color, callback);
            }
        }
    };

    var dfsVisit = function(u, color, callback){

        color[u] = 'grey';
        if (callback) {
            callback(u);
        }
        console.log('Discovered ' + u);
        var neighbors = adjList.get(u);
        for (var i=0; i<neighbors.length; i++){
            var w = neighbors[i];
            if (color[w] === 'white'){
                dfsVisit(w, color, callback);
            }
        }
        color[u] = 'black';
        console.log('explored ' + u);
    };


    this.BFS = function(v){

        var color = initializeColor(),
            queue = new Queue(),
            d = {},
            pred = {};
        queue.enqueue(v);

        for (var i=0; i<vertices.length; i++){
            d[vertices[i]] = 0;
            pred[vertices[i]] = null;
        }

        while (!queue.isEmpty()){
            var u = queue.dequeue(),
                neighbors = adjList.get(u);
            color[u] = 'grey';
            for (i=0; i<neighbors.length; i++){
                var w = neighbors[i];
                if (color[w] === 'white'){
                    color[w] = 'grey';
                    d[w] = d[u] + 1;
                    pred[w] = u;
                    queue.enqueue(w);
                }
            }
            color[u] = 'black';
        }

        return {
            distances: d,
            predecessors: pred
        };
    };

    var time = 0;
    this.DFS = function(){

        var color = initializeColor(),
            d = {},
            f = {},
            p = {};
        time = 0;

        for (var i=0; i<vertices.length; i++){
            f[vertices[i]] = 0;
            d[vertices[i]] = 0;
            p[vertices[i]] = null;
        }

        for (i=0; i<vertices.length; i++){
            if (color[vertices[i]] === 'white'){
                DFSVisit(vertices[i], color, d, f, p);
            }
        }

        return {
            discovery: d,
            finished: f,
            predecessors: p
        };
    };

    var DFSVisit = function(u, color, d, f, p){

        console.log('discovered ' + u);
        color[u] = 'grey'
您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • !!!重要剖析死鎖原理
    原鏈接 作者:大漠孤煙直 背景及現象 線上生產環境在某些時候經常性的出現資料庫操作死鎖，導致業務人員無法進行操作。經過DBA的分析，是某一張表的insert操作和delete操作發生了死鎖。簡單介紹下資料庫的情況（因為涉及到真實數據，這裡做了模擬，不影響具體的分析和分析的結果。）假設存在如下2張表： ...
  • Neo4j學習筆記(1)——使用Java API實現簡單的增刪改查
    項目的創建及配置 因為Neo4j依賴的jar包比較多，所以推薦使用Maven來管理。 首先創建一個Maven Project，添加依賴： 使用的是3.2.6版本，對應版本的Neo4j安裝地址摸我。 使用嵌入式資料庫 配置好之後，就可以開始了，第一步是學習開啟和關閉資料庫。 無論是創建一個新的資料庫， ...
  • 與apk簽名有關的那些概念與命令
    一、概念篇 1、消息摘要-Message Digest 消息摘要：在消息數據上，執行一個單向的hash函數，生成一個固定長度的hash值，這個Hash值就是消息摘要，也成為數字指紋。 消息摘要特點： （1）無論輸入消息多長，計算出來的消息摘要長度總是固定的； （2）不可逆性，通過摘要無法推算出消息本 ...
  • iOS----------UITextField實現過濾選中狀態拼音
    2018年上班的第二天，就這樣背了一個大鍋。我們項目中有一個搜索功能，在這一期的版本中，為了增強優化，去除了過濾空格的請求，這樣或許能增加很好的用戶體驗，恰恰相反，偷雞不成蝕把米。沒想到蘋果系統的輸入法竟然能自動聯想，在沒有選擇漢字的時候，竟然能聯想出來一大堆智能拼音，what？？？還有這種操作？？ ...
  • Java編程規範
    從一開始接觸編程就多次聽到編程得養成好的編碼習慣。的確，不讓好的編碼成為習慣，也就只能在隨意的代碼風格裡放縱了（網上瀏覽到的代碼是有這樣的吧）。 在網上也看了很多人的總結，學到很多。將其中的部分進行彙總，這次的隨筆大部分只是文字的搬運工，如有誤還請指正。 一.標識符命名(儘量以最少的字元表達完整的含 ...
  • 【quickhybrid】iOS端的項目實現
    前言 18年元旦三天內和朋友突擊了下，勉強是將雛形做出來了，後續的API慢慢完善。（當然了，主力還是那個朋友，本人只是初涉iOS，勉強能看懂，修修改改而已） 大致內容如下： JSBridge核心交互部分 、`page`等部分常用API的實現（其它慢慢完善） 組件（自定義）API拓展的實現 API的權 ...
  • Android熱修複之 - 阿裡開源的熱補丁
    1.1 基本介紹 我們先去github上面瞭解它https://github.com/alibaba/AndFix 請原諒我的盜圖行為，英文解釋我就不貼了我自己也看不懂，大致的意思的就是要想盡一切辦法給導致我們崩潰的那個類的某個方法去動手術把它弄好，而這裡就有一個概念那就AndFix.apatch補 ...
  • AJAX請求真的不安全麽？談談Web安全與AJAX的關係。
    開篇三問 1. AJAX請求真的不安全麽？ 2. AJAX請求哪裡不安全？ 3. 怎麼樣讓AJAX請求更安全？ 前言 本文包含的內容較多，包括AJAX，CORS，XSS，CSRF等內容，要完整的看完並理解需要付出一定的時間。 另外，見解有限，如有描述不當之處，請幫忙及時指出。 __正文開始...__ ...
一周排行
    -Advertisement-
    Play Games
  • 移動開發（一）：使用.NET MAUI開發第一個安卓APP
    移動開發（一）：使用.NET MAUI開發第一個安卓APP 對於工作多年的C#程式員來說，近來想嘗試開發一款安卓APP，考慮了很久最終選擇使用.NET MAUI這個微軟官方的框架來嘗試體驗開發安卓APP，畢竟是使用Visual Studio開發工具，使用起來也比較的順手，結合微軟官方的教程進行了安卓 ...
  • wpf ToggleButton選中效果和一個登錄界面
    前言 QuestPDF 是一個開源 .NET 庫，用於生成 PDF 文檔。使用了C# Fluent API方式可簡化開發、減少錯誤並提高工作效率。利用它可以輕鬆生成 PDF 報告、發票、導出文件等。 項目介紹 QuestPDF 是一個革命性的開源 .NET 庫，它徹底改變了我們生成 PDF 文檔的方 ...
  • 彈幕樹洞項目功能新增篇
    項目地址 項目後端地址： https://github.com/ZyPLJ/ZYTteeHole 項目前端頁面地址： ZyPLJ/TreeHoleVue (github.com) https://github.com/ZyPLJ/TreeHoleVue 目前項目測試訪問地址： http://tree ...
  • 第27篇 sqlserver2022詳細安裝步驟
    話不多說，直接開乾 一.下載 1.官方鏈接下載： https://www.microsoft.com/zh-cn/sql-server/sql-server-downloads 2.在下載目錄中找到下麵這個小的安裝包 SQL2022-SSEI-Dev.exe，運行開始下載SQL server； 二. ...
  • .NET 開源高性能 MQTT 類庫
    前言 隨著物聯網（IoT）技術的迅猛發展，MQTT（消息隊列遙測傳輸）協議憑藉其輕量級和高效性，已成為眾多物聯網應用的首選通信標準。 MQTTnet 作為一個高性能的 .NET 開源庫，為 .NET 平臺上的 MQTT 客戶端與伺服器開發提供了強大的支持。 本文將全面介紹 MQTTnet 的核心功能 ...
  • Serilog文檔翻譯系列（六） - 可用的接收器、增強器、格式化輸出
    Serilog支持多種接收器用於日誌存儲，增強器用於添加屬性，LogContext管理動態屬性，支持多種輸出格式包括純文本、JSON及ExpressionTemplate。還提供了自定義格式化選項，適用於不同需求。 ...
  • 警惕 Visual Studio 屬性求值副作用導致邏輯不符合預期
    目錄簡介獲取 HTML 文檔解析 HTML 文檔測試參考文章 簡介 動態內容網站使用 JavaScript 腳本動態檢索和渲染數據，爬取信息時需要模擬瀏覽器行為，否則獲取到的源碼基本是空的。 本文使用的爬取步驟如下： 使用 Selenium 獲取渲染後的 HTML 文檔 使用 HtmlAgility ...
  • [使用目前最新版]HybridCLR6.9.0+YooAsset2.2.4實現純C# Unity熱更新方案 (一)
    1.前言 什麼是熱更新 游戲或者軟體更新時，無需重新下載客戶端進行安裝，而是在應用程式啟動的情況下，在內部進行資源或者代碼更新 Unity目前常用熱更新解決方案 HybridCLR，Xlua，ILRuntime等 Unity目前常用資源管理解決方案 AssetBundles，Addressable， ...
  • 在 ASP.NET Core Web API 中使用操作篩選器統一處理通用操作
    本文章主要是在C# ASP.NET Core Web API框架實現向手機發送驗證碼簡訊功能。這裡我選擇是一個互億無線簡訊驗證碼平臺，其實像阿裡雲，騰訊雲上面也可以。 首先我們先去 互億無線 https://www.ihuyi.com/api/sms.html 去註冊一個賬號 註冊完成賬號後，它會送 ...
  • 第28篇 如何.net中實現高效可靠數據同步api
    通過以下方式可以高效，並保證數據同步的可靠性 1.API設計 使用RESTful設計，確保API端點明確，並使用適當的HTTP方法（如POST用於創建，PUT用於更新）。 設計清晰的請求和響應模型，以確保客戶端能夠理解預期格式。 2.數據驗證 在伺服器端進行嚴格的數據驗證，確保接收到的數據符合預期格 ...
所有分類