歡迎探討，如有錯誤敬請指正

如需轉載，請註明出處http://www.cnblogs.com/nullzx/

1. 歸併排序演算法的使用情景

歸併排序演算法和快速排序演算法是java.util.Arrays中使用的排序算。對於一般的基本數據類型，Arrays.sort函數使用雙軸快速排序演算法，而對於對象類型使用歸併排序（準確的說使用的是TimSort排序演算法，它是歸併排序的優化版本）。這樣做的原因有兩點，第一個原因，歸併排序是穩定的，而快速排序不是穩定的。第二個原因，對於基本數據類型，排序的穩定性意義不大，但對於複合數據類型（比如對象）排序的穩定性就能幫助我們保持排序結果的某些性質。

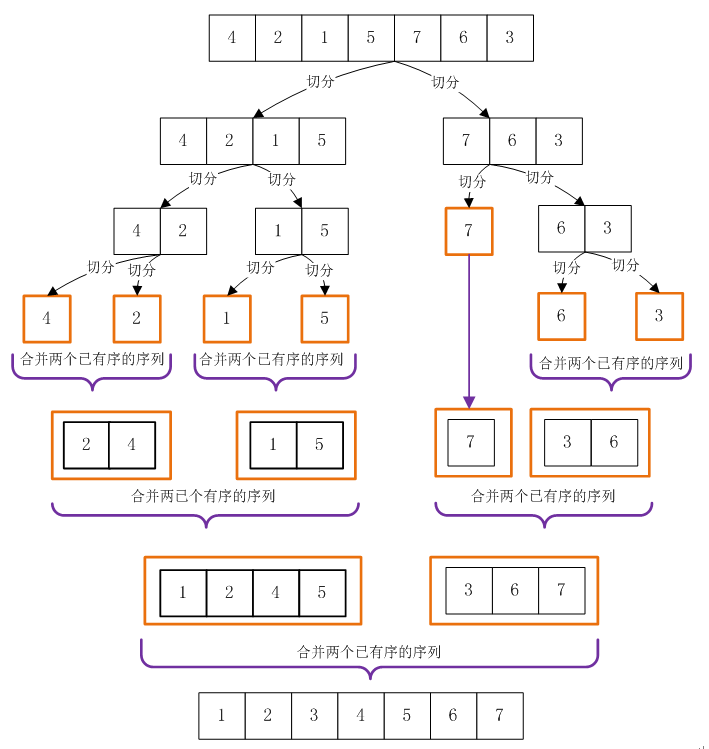
2. 自頂向下的歸併排序

自頂向下的排序演算法就是把數組元素不斷的二分，直到子數組的元素個數為一個，因為這個時候子數組必定是已有序的，然後將兩個有序的序列合併成一個新的有序的序列，兩個新的有序序列又可以合併成另一個新的有序序列，以此類推，直到合併成一個有序的數組。

為了體現歸併的排序的穩定性，我們的代碼使用java的泛型來實現對任意對象的排序。

	public static <T extends Comparable<? super T>> 
	void MergeSortUpToDown(T[] A){
		@SuppressWarnings("unchecked")
		//創建合併兩個有序序列的輔助數組
		T[] aux = (T[])Array.newInstance(A.getClass().getComponentType(), A.length);
		mergeSortUpToDown0(A, aux, 0, A.length-1);
	}
	
	public static <T extends Comparable<? super T>> 
	void mergeSortUpToDown0(T[] A, T[] aux, int start, int end){
		if(start == end)
			return;
		int mid = (start+end)/2;
		mergeSortUpToDown0(A, aux, start, mid);
		mergeSortUpToDown0(A, aux, mid+1, end);
		//複製到輔助數組中,此時[start,mid] [mid+1, end]兩個子數組已經有序
		System.arraycopy(A, start, aux, start, end - start + 1);
		//然後歸併回來
		int i = start, j = mid+1, k;
		for(k = start; k <= end; k++){
			if(i > mid){
				A[k] = aux[j++];
			}else
			if(j > end){
				A[k] = aux[i++];
			}else
			if(aux[i].compareTo(aux[j]) <= 0){
				A[k] = aux[i++];
			}else{
				A[k] = aux[j++];
			}
		}
	}

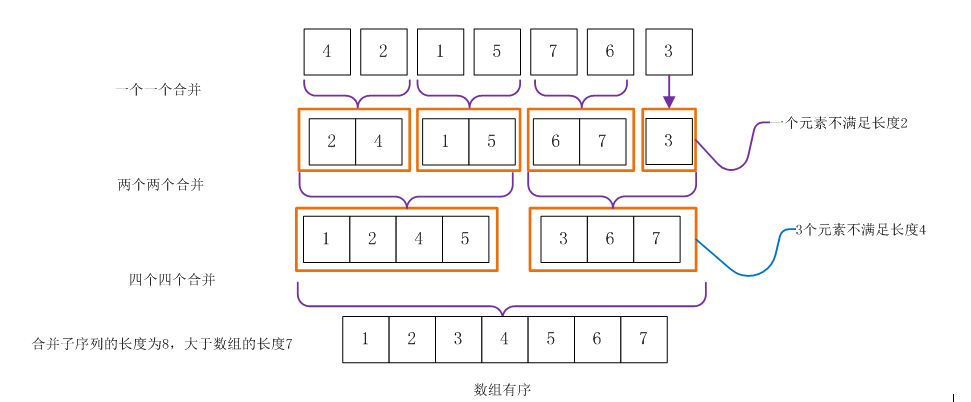
3. 自底向上的歸併排序

自底向上的歸併排序演算法的思想就是數組中先一個一個歸併成兩兩有序的序列，兩兩有序的序列歸併成四個四個有序的序列，然後四個四個有序的序列歸併八個八個有序的序列，以此類推，直到，歸併的長度大於整個數組的長度，此時整個數組有序。需要註意的是數組按照歸併長度劃分，最後一個子數組可能不滿足長度要求，這個情況需要特殊處理。自頂下下的歸併排序演算法一般用遞歸來實現，而自底向上可以用迴圈來實現。

	//自底向上歸併排序
	public static <T extends Comparable<? super T>> void MergeSortDownToUp(T[] A){
		@SuppressWarnings("unchecked")
		T[] aux = (T[])Array.newInstance(A.getClass().getComponentType(), A.length);
		int len,i,j,k,start,mid,end;
		//len表示歸併子數組的長度，1表示，一個一個的歸併，歸併後的長度為2,2表示兩個兩個的歸併，歸併後的長度為4,以此類推
		for(len = 1; len < A.length; len = 2*len){
			//複製到輔助數組中
			System.arraycopy(A, 0, aux, 0, A.length);
			//按照len的長度歸併回A數組，歸併後長度翻倍
			for(start = 0; start < A.length; start = start+2*len){
				mid = start + len - 1;
				//對於數組長度不滿足2的x次冪的數組，mid可能會大於end
				end = Math.min(start + 2*len - 1, A.length-1);
				i = start; 
				//mid大於end時,j必然大於end,所以不會引起越界訪問
				j = mid+1;
				//[start,mid] [mid+1, end]
				for(k = start; k <= end; k++){
					if(i > mid){
						A[k] = aux[j++];
					}else
					if(j > end){
						A[k] = aux[i++];
					}else
					if(aux[i].compareTo(aux[j]) < 0){
						A[k] = aux[i++];
					}else{
						A[k] = aux[j++];
					}
				}
			}
		}
	}

4. 參考文章

[1] 演算法（第四版）RobertSedgewick