這個遞歸不太難相信大家都知道什麼是遞歸，但在實際開發的時候用過多少次遞歸呢？程式的世界有句話叫“人用迴圈，神用遞歸”，很多情況下我們都會優先使用迴圈而不是遞歸。我和幾個朋友聊過，他們的看法是：“相比迴圈而言，遞歸性能更差，而且更不可控，容易出問題。” 捕獲關鍵詞“問題”，啟動“解決”模式... ...

這個遞歸不太難

相信大家都知道什麼是遞歸，但在實際開發的時候用過多少次遞歸呢？

程式的世界有句話叫“人用迴圈，神用遞歸”，很多情況下我們都會優先使用迴圈而不是遞歸。我和幾個朋友聊過，他們的看法是：“相比迴圈而言，遞歸性能更差，而且更不可控，容易出問題。”

捕獲關鍵詞“問題”，啟動“解決”模式...

一、先熱個身

數學家高斯的在念小學的時候，他的數學老師出了一道題：對自然數1到100求和。高斯用首尾相加的辦法很快的算出了答案，不過我們這次要扮演高斯的同學，老老實實的從1加到100。

首先試一下迴圈的思路：

function sum(n) {
    let count = 0;
    for (let i = 1; i <= n; i++) {
    	count += i;
    }
    return count;
}
sum(100); // 5050

可以看到迴圈體只有一行代碼

count += i;

如果把 count 當成是一個函數的返回值，一個基本的遞歸邏輯就成型了：

function sum(n) {
    return n + sum(n-1);
}
// 這裡的 sum(n-1) 不能寫成 sum(n--)

但僅僅這樣是不夠的，還差一個關鍵代碼塊——開關

遞歸本身是一個無限迴圈，需要添加控制條件，讓程式在合適的時候退出迴圈

function sum(n) {
		if (n === 1) {
			return n;
		}
    return n + sum(n-1);
}
sum(100); // 5050

試試 sum(20000) 的結果是多少？

二、三大要素

上面的例子已經完成了一個簡單的遞歸，回頭總結一下，我們主要做了兩件事：

遞歸的拆解 —— 提取重覆的邏輯，縮小問題規模
遞歸的出口 —— 明確遞歸的結束條件

其實在這之前，我們還做了一件事，這件事很重要，但常常會被我們忽略掉：

遞歸的定義 —— 明確函數的功能

這三大要素是寫遞歸的必要條件，而其中的第三點，是寫好一個遞歸的必要條件。

以經典的樹組件作為案例，來印證一下這三要素。

樹組件的主要功能，就是將一個規範的具有層級的數組，渲染成樹列表

由此我們能明確這個函數的主要功能：接收一個數組入參，返回一個完整的樹組件

好像大概可能應該也許有點問題？

還是先來觀察數組吧。每個元素的 title 和 key 是固定的，只是非葉子節點有 children。而 children 內部的結構也是 title 和 key，加一個可能有的 children。

這樣一來就能很容易的提取出重覆的邏輯：渲染樹節點，以 children 作為遞歸結束的判斷條件。

為了更好的 UI 展示，還需要記錄樹節點的層級來計算當前節點的縮進。

我們只是在渲染樹節點，而不是渲染整個樹！

之所以能渲染出整個樹，是因為在函數執行的過程中，產生了很多的樹節點，這些樹節點組成了一個樹。

所以我們這個函數功能應該是：接收一個數組作為必要參數，和一個數值作為可選參數，並返回一個樹節點。

重新捋一下思路，這個渲染樹組件的函數就清晰多了：

renderTree = (list, level = 1) => {
  return list.map(x => {
    const { children, id } = x || {};
    if (children) { // 遞歸的結束條件
      return (
        <TreeNode key={`${id}`} level={level}>
          {/* 調用自身，形成遞歸 */}
          {renderTreeNodes(children, level + 1)}
        </TreeNode>
      );
    }
    // 遞歸的出口
    return <TreeNode key={`${id}`} level={level}></TreeNode>
  })
}

三、遞歸優化 - 手動緩存

當我們去分析一個迴圈的時候，能清晰的看出這個函數的內部邏輯和執行次數。

而遞歸則不然，它的結構更加簡潔，但也增加了理解成本。比如下麵這個遞歸，你能一眼看出它的執行次數麽？

function Fibonacci (n) {
  return n <= 2 ? 1 : Fibonacci(n - 1) + Fibonacci(n - 2);
}

這就是著名的 Fibonacci 數列，我儘力避免拿它舉例，後來發現這個例子最為簡單直觀。

Fibonacci 數列：1, 1, 2, 3, 5, 8, 13, 21...

f(n) = f(n-1) + f(n-2)

我們試著執行一下 Fibonacci(10)，並記錄該函數的調用次數

居然執行了 109 次？

其實回頭分析一下 Fibonacci 這個函數就能發現，執行的時候存在很多的重覆計算，比如計算 Fibonacci(5)：

-- f(5)
| -- f(4)
| | -- f(3)
| | | -- f(2)
| | | -- f(1)
| | -- f(2)
| -- f(3)
| | -- f(2)
| | -- f(1)

葉子節點會被重覆計算，層次越深，計算的次數就越多

這裡有兩個優化思路，第一種是從當前的邏輯上，添加一層緩存，如果當前入參已經計算過，就直接返回結果。

// 緩存函數
function memozi(fn){
	const obj = {};
  return function(n){
    obj[n] = obj[n] || fn(n);
    return obj[n];
  }
}

const Fibonacci = memozi(function(n) {
  return n <= 2 ? 1 : Fibonacci(n - 1) + Fibonacci(n - 2);
})

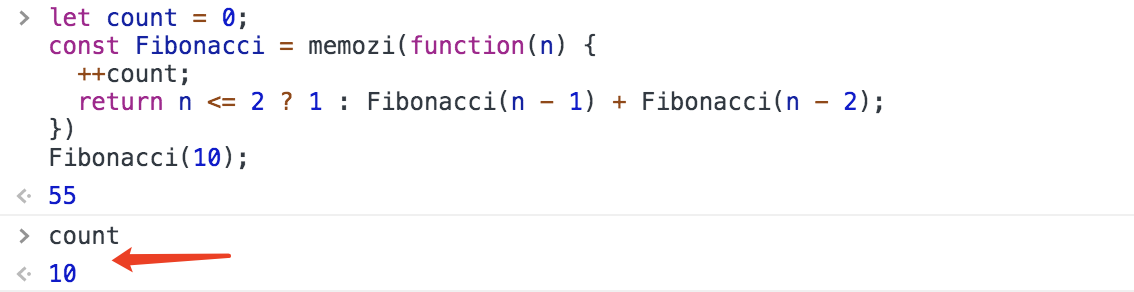
只執行了10次！這已經達到了迴圈的執行次數。

這是一種空間換時間的思想，增加了額外的變數來記錄狀態，不過函數的實際調用次數並沒有減少，只是在 memozi 函數中做了判斷。

怎麼才能真正實現 O(n) 的時間複雜度呢？

四、遞歸優化 - 自下而上

上面所有的遞歸都是自上而下的遞歸，從 n 開始，一直計算到最小值。但在 Fibonacci 的例子中，如果需要計算 f(n)，就需要先計算 f(n-1)，所以一定會存在重覆計算的情況。

能不能從最小值開始計算呢？

在明確了 f(n) = f(n-1) + f(n-2) 規則的前提下，同時又知道 f(1) = 1, f(2) = 1，那就能推斷出 f(3) = 2，乃至 f(4), f(5)...

從而得到一個基本邏輯：

function foo(x = 1, y = 1) {
  return foo(y, x + y);
}

這裡的 x 和 y 就是對應 n=1 和 n=2 的時候的值，然後逐步計算出 n=3, n=4... 的值。

然後加入 n <= 2 的邊界，得到最終的遞歸函數：

function Fibonacci(n, x = 1, y = 1) {
  return n <= 2 ? y : Fibonacci(n - 1, y, x + y);
}

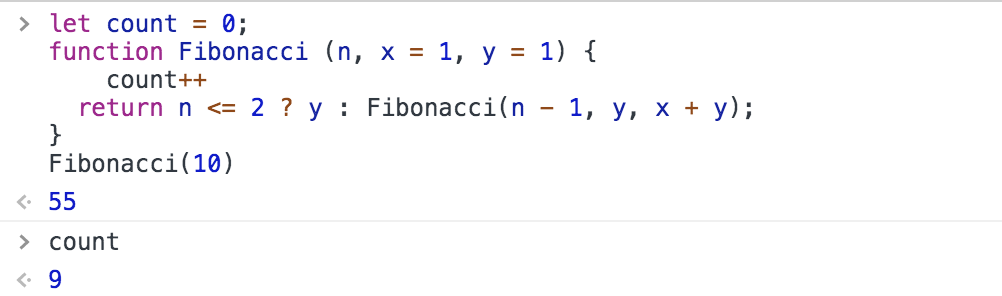
我們僅僅是稍微調整了函數的邏輯，就達到了 O(n) 的時間複雜度。這種自下而上的思想，其實是動態規劃的體現。

動態規劃是一種尋求最優解的數學方法，它經常會被當做一種演算法，但它其實並不像“二分查找”、“冒泡排序”一樣有著固定的範式。實際上動態規劃是一種方法論，它提供的是一種解決問題的思路。

簡單來說，動態規劃將一個複雜的問題分解成若幹個子問題，通過綜合子問題的最優解來得到原問題的最優解。而且動態規劃是自下而上求解，先計運算元問題，再由這些子問題計算父問題，直至求解出原問題的解，將時間複雜度優化為 O(n)。

動態規劃有三個重要概念：

最優子結構
邊界

光看名詞就覺得有點似曾相識。沒錯，這就是前文提到的遞歸三要素中的“縮小問題規模”和“結束條件”。

而動態規劃的第三個概念，才是其核心所在：

狀態轉移方程

所謂狀態轉移方程，就是子問題與父問題之間的關係，或者說：如何用子問題推導出父問題。

通常我們用遞歸都是自上而下，是先遇到了父問題，再去解決子問題。而動態規劃是先解決子問題，再通過狀態轉移方程求解出父問題，也就是自下而上。這種自下而上的遞歸也被稱為“遞推”。

動態規劃的適用範圍，也是自下而上的適用範圍：

存在最優子結構

作為整個過程的最優策略，應當具有這樣的特質：無論過去的狀態和決策如何，相對於前面的決策所形成的狀態而言，餘下的決策序列必然構成最優子策略。

也就是說，一個最優策略的子策略也是最優的。
無後效性

如果某階段狀態給定後，則在這個階段以後過程的發展不受這個階段以前各段狀態的影響。

也就是說，計算f(i)，不需要f(i+1)...f(n)的值，也不會修改f(1)...f(i-1)的值（1 < i < n）。

只要滿足這兩點，就可以用自下而上的思路來優化。

不過上面自下而上求解 Fibonacci 數列的函數，除了動態規劃之外，還使用了尾調用。

五、遞歸優化 - 尾調用

函數在調用的時候，會在調用棧 (call stack) 中存有記錄，每一條記錄叫做一個調用幀 (call frame)。每調用一個函數，就向棧中 push 一條記錄，函數執行結束後依次向外彈出，直到清空調用棧。

function foo () { console.log('wise'); }
function bar () { foo(); }
function baz () { bar(); }

baz();

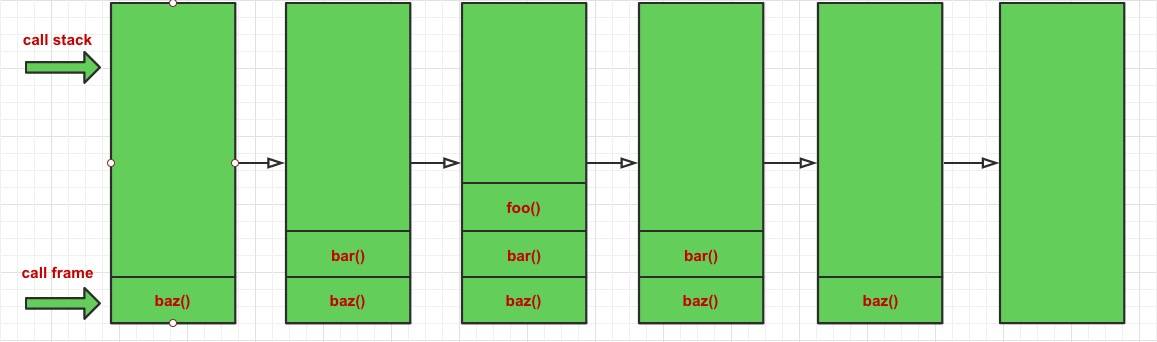
造成這種結果是因為每個函數在調用另一個函數的時候，並沒有 return 該調用，所以 JS 引擎會認為你還沒有執行完，會保留你的調用幀。

如果對上面的例子做如下修改：

function foo () { console.log('wise'); }
function bar () { return foo(); }
function baz () { return bar(); }

baz();

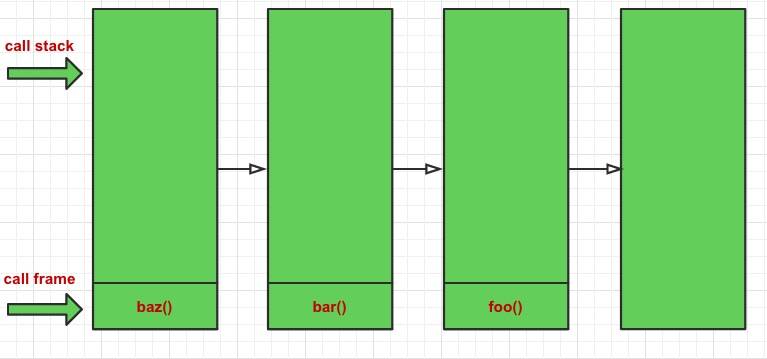
上面的改動其實是函數式編程中的一個重要概念，當一個函數執行時的最後一個步驟是返回另一個函數的調用，這就叫做尾調用(PTC)。如果是在遞歸裡面使用，即在函數的末尾調用自身，就是尾遞歸。

回頭來看最開始的求 1~n 之和的例子：

function sum(n) {
		if (n === 1) {
			return n;
		}
    return n + sum(n-1);
}
sum(100); // 5050

如果執行 sum(20000) 會棧溢出（爆棧）:

Uncaught RangeError: Maximum call stack size exceeded

將這個遞歸升級為尾遞歸：

function sum(n, count = 0) {
		if (n === 1) {
			return count + n;
		}
    return sum(n-1, count+n);
}

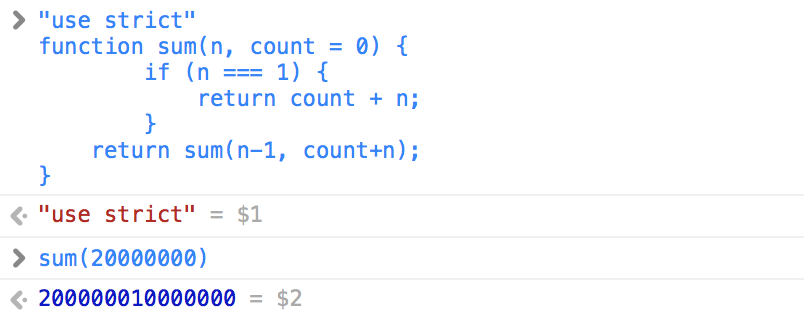
現在調用棧中的調用幀始終只有一條，相對節省記憶體，這樣的遞歸就靠譜了許多

尾調用對遞歸的意義重大，但在實際運用的時候卻備受阻礙。

首先需要使用嚴格模式"use strict"，其次主流瀏覽器只有 Safari 支持尾調用（上面的截圖就是在 Safari 截的），Chrome 和 Firefox 甚至 node 都不支持尾調用優化。

Chrome V8 團隊給出的解釋是：

由於尾調用消除調用幀是隱式的，這意味著開發者可能很難發現一些無限迴圈的遞歸，如果它們恰好出現在末尾，因為這些遞歸的堆棧將不再溢出。
尾調用會丟失堆棧信息，這將導致執行流中的堆棧信息丟失，這將影響程式調試和錯誤收集。

不過即使如此，Chrome 和 Mozilla 依然認可尾調用優化所帶來的的性能提升，只是在引擎層面還沒有找到一個很安全可靠的方案來支持尾調用優化。微軟曾經提議從語法上來指定尾調用（類似於 return continue 這樣的特殊語句），不過最終方案仍在討論中。

雖然大部分的瀏覽器還不支持尾遞歸，但我們在開發的時候依然可以優先使用尾調用，畢竟運行的效果是一樣的，而一旦程式在支持尾遞歸的環境下運行，就會有更快的運行速度。更重要的是，當我們嘗試使用尾遞歸的時候，通常會自然而然的用到自下而上的思想。

六、小結

我們一般認為遞歸會比迴圈的性能要差，是因為函數調用本身是有開銷的。

但如果能實現尾遞歸，那麼遞歸的效率應該至少和迴圈一樣好。

對於不能使用尾調用的遞歸，即使寫成了迴圈的形式，也只是拿一個棧來模擬遞歸的過程。會帶來一定的效率提升，但也會造成代碼的冗餘。

關於迴圈和（優化之後的）遞歸之間的取捨，我覺得可以從以下幾個方面判斷：

遞歸的優點是代碼簡潔，邏輯清晰。缺點是調用幀導致的執行效率過低，而且不如迴圈容易理解；
遞歸和迴圈完全可以互換，但遞歸可以處理的問題，如果通過迴圈去解決，通常需要額外的低效處理；
如果邏輯相對簡單，使用迴圈也很簡潔，可以優先考慮迴圈；
在無法使用尾遞歸的環境，迴圈永遠是優先考慮的解決方案，但如果能接受遞歸的性能開銷，建議使用遞歸。

我認為遞歸其實是一種思維方式。所謂的“遞歸比迴圈慢”，指的是遞歸的各種實現。

掌握遞歸的意義不在於編碼本身，而在於知道如何編碼。

Premature optimization is the root of all evil.

過早優化是萬惡之源。

—— 《電腦編程藝術》Donald Knuth

參考資料：

《遞歸優化：尾調用和Memoization》—— LumiereXyloto

《尾調用優化》—— 阮一峰

《【譯】V8 團隊眼中的 ES6、ES7及未來》—— 奇舞團

《什麼是動態規劃（Dynamic Programming）？動態規劃的意義是什麼？》—— 苗華棟