[導讀]:前面一篇文章關於IIR/移動平均濾波器設計的文章。本文來聊一聊陷波濾波器,該濾波器在混入諧波干擾時非常有用,演算法簡單,實現代價低。本文來一探其在機理、應用場景。 註:儘量在每篇文章寫寫摘要,方便閱讀。信息時代,大家時間都很寶貴,如此亦可節約粉絲們的寶貴時間。 前文所說學習的倡導2W1H原則 ...
[導讀]:前面一篇文章關於IIR/移動平均濾波器設計的文章。本文來聊一聊陷波濾波器,該濾波器在混入諧波干擾時非常有用,演算法簡單,實現代價低。本文來一探其在機理、應用場景。
註:儘量在每篇文章寫寫摘要,方便閱讀。信息時代,大家時間都很寶貴,如此亦可節約粉絲們的寶貴時間。
前文所說學習的倡導2W1H原則,思來想來並不全面,本文決定從What Why Where When How幾個維度展開。我稱之為4W1H學習法,借鑒管理學領域中的5W1H,起源於1932年,美國政治學家拉斯維爾提出“5W分析法”,後延伸出5W1H法。有興趣的可以找來閱讀,題外話技術人員讀一些方法論管理學方面的書籍於做人做事個人認為是非常有益的。
梳狀濾波器之What?
在信號處理中,梳狀濾波器是通過向其自身添加信號的延遲而實現的,從而造成增強或削弱干擾的濾波器。 梳狀濾波器的頻率響應由一系列規則間隔的凹口組成,從而呈現出梳狀外觀。其大體拓撲形式如下:

梳狀濾波器有著大量不同形式的傳遞函數,其作用是對周期性信號增強或削弱周期性信號,本文主要介紹其中一種形式的Z傳遞函數\(H(Z)=b\frac{1-Z^{-N}}{1-{\rho}N^{-N}}\)
其中:\(b=\frac{1+\rho}{2}\)
其信號流圖如下:
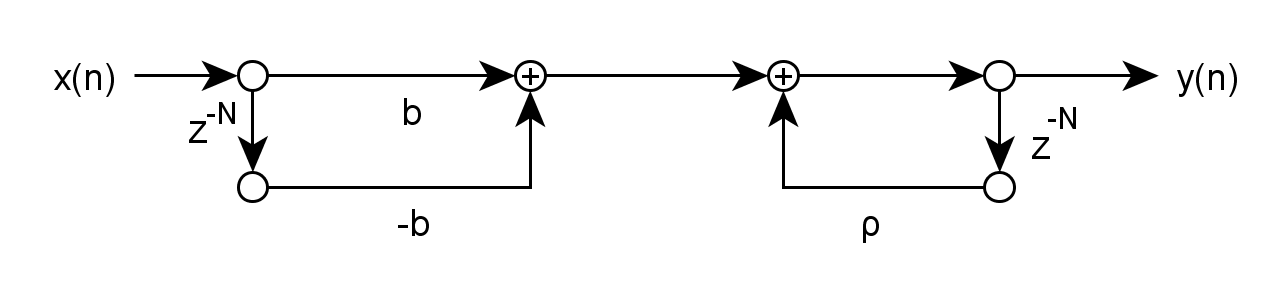
梳狀濾波器英文稱為comb(梳子) filter,這個名字真是無與倫比的絕!為何?談到濾波器一定會重點關註其對幅頻響應曲線,梳狀濾波器,正是描述其幅頻響應的。而幅頻響應從本質上講是描述系統各頻率能量的放大或者衰減。本文中談到的濾波器就是一個系統,對其輸入能量按頻率不同進行放大或者衰減,從而起到過濾作用。
梳狀濾波器之Why?
前面說到梳狀濾波器其幅頻響應樣子和梳子長的很像,為啥長的像,來一探究竟:
其頻率響應為:
\[H(e^{j\omega})=b\frac{1-e^{j\omega{N}}}{1-\rho{e^{j\omega{N}}}} \]
現以採樣率20000Hz,10階,阻帶帶寬50Hz為例。其幅頻響應曲線如下:
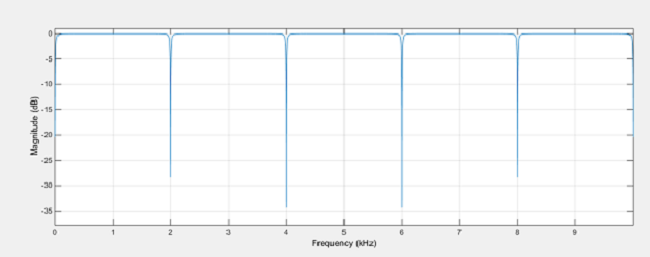
相頻響應曲線為:

從幅頻響應曲線可看出,其形狀真是如梳子形狀,當階數越大,其齒數越多。這種形式的梳狀濾波器對於2KHz,4KHz,6KHz,8KHz,10KHz信號是衰減作用,也即阻止該頻率通過,阻帶寬度為50Hz。前面談到了我們可以對某些頻率信號加強,而其他的信號衰減吸收。這裡引申出其互補濾波器,其Z傳遞函數剛好有一點形式上的對稱性:
\[H(Z)=b\frac{1+Z^{-N}}{1-{\rho}N^{-N}} \]
其中b為:
\[b=\frac{1-\rho}{2} \]
此互補濾波器其幅頻響應曲線為:
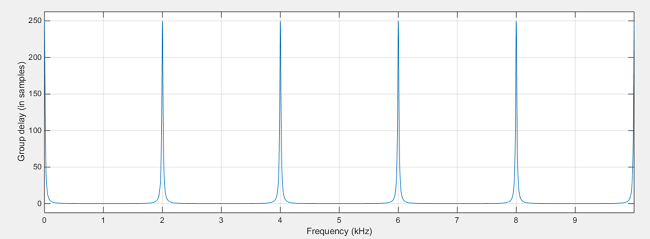
這兩個濾波器從其幅頻響應曲線剛好是互補對稱的。至此,從原理上已基本明瞭為什麼稱其為梳狀濾波器。
梳狀濾波器就其本質也是一種IIR濾波器,因為濾波器的輸出反饋參與了濾波運算。
梳狀濾波器之Where?
費這麼大勁研究梳狀濾波器,須的知道在什麼地方可以去使用它,事實上梳狀濾波器有著大量的應用場合:
- 級聯積分梳狀(CIC)濾波器,通常用於插值和抽取操作期間的抗混疊,這些操作會更改離散時間系統的採樣率。
- PAL和NTSC電視解碼器的晶元(也可能是軟體濾波)實現的2D和3D梳狀濾波器用以降低網點偽影干擾。
- 音頻信號處理,包括延遲,鑲邊和數字波導合成中大量應用。 例如,如果將延遲設置為幾毫秒,則可以使用梳狀濾波器對圓柱空腔或振動弦中的聲駐波的影響進行建模。
- 在天文學中,天體梳濾波器有望將現有光譜儀的精度提高近一百倍。
- 在聲學方面,梳齒濾波會以某些不需要的方式出現。 例如,當兩個揚聲器在距收聽者不同距離處播放同一信號時,會對信號產生梳狀濾波效果。 在任何封閉的空間中,聽眾會聽到直接聲音和反射聲音的混合聲音。 由於反射的聲音路徑較長,因此構成了直接聲音的延遲版本,並創建了一個梳狀濾波器,使兩者在聽眾處合併。
- 儀器儀錶也常用梳狀濾波器消除諧波干擾,或者選頻放大。
- ......
梳狀濾波器之How?
本文依然藉助於matlab的fdatool進行設計示例:
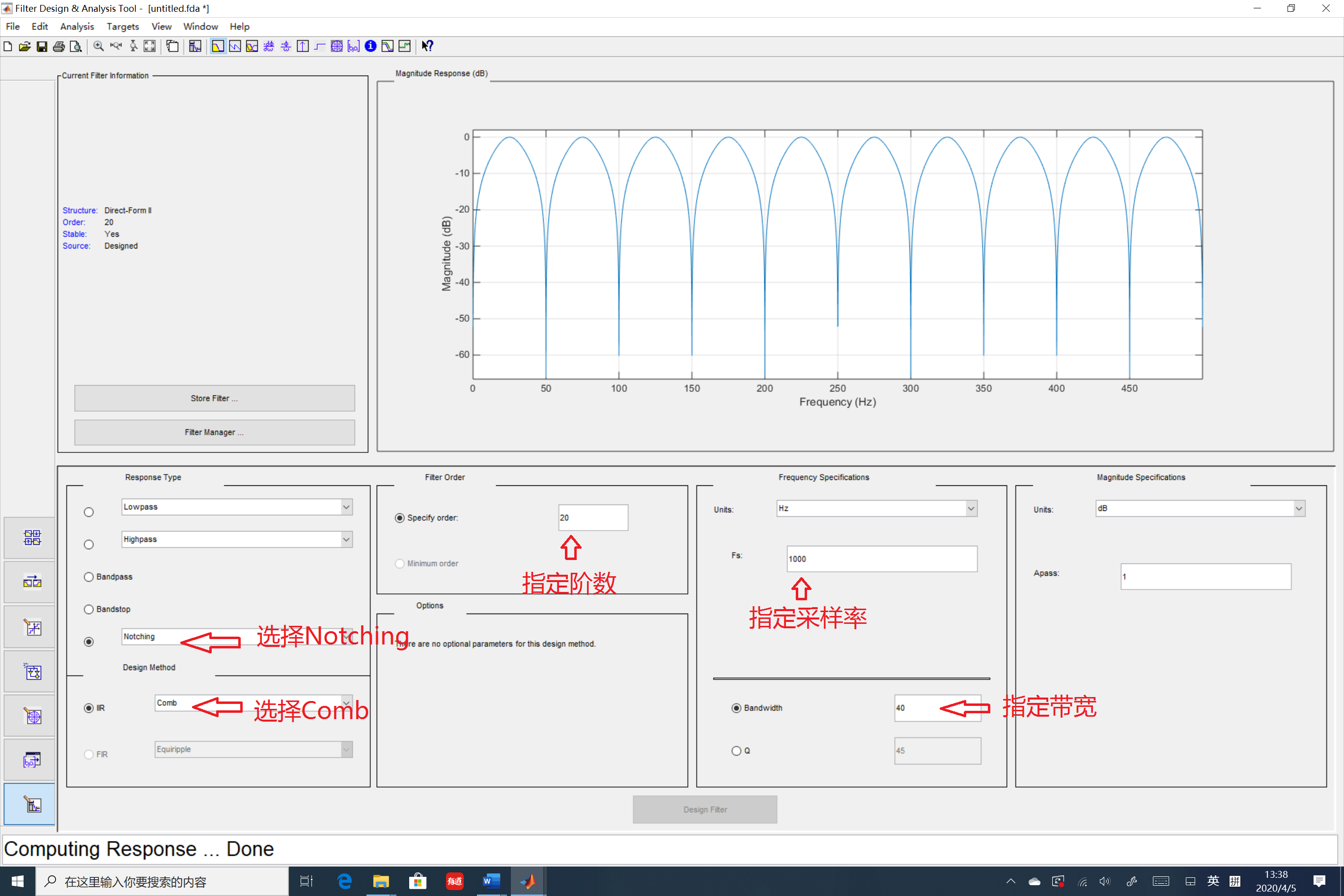
將其重要設置標註如上,其他的與IIR一文類似,就不羅嗦舉例了。將重要參數輸入,點擊設計就輕鬆設計出相應的濾波器參數了。這裡以1000Hz採樣率,40Hz帶寬,20階為例,設計出濾波器參數如下:
% Generated by MATLAB(R) 8.4 and the Signal Processing Toolbox 6.22.
% Generated on: 05-Apr-2020 13:40:29
% Coefficient Format: Decimal
% Discrete-Time IIR Filter (real)
% -------------------------------
% Filter Structure : Direct-Form II
% Numerator Length : 21
% Denominator Length : 21
% Stable : Yes
% Linear Phase : No
Numerator:
0.38970091175151578
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
-0.38970091175151578
Denominator:
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0.22059817649696845
C語言實現非常簡單,由於梳狀濾波器本質上是IIR濾波器,所以也可以直接利用前文ARM的庫函數實現部署。由前面Z傳遞函數,很容易推導出其差分方程如下:
\[\begin{align*} y(n)&=bx(n)-bx(n-N)+\rho{y(n-N)}\\&=\frac{1+\rho}{2}[x(n)-x(n-N)]+\rho{y(n-N)} \end{align*} \]
其互補濾波器差分方程為:
\[\begin{align*} y(n)&=bx(n)-bx(n-N)+\rho{y(n-N)}\\&=\frac{1-\rho}{2}[x(n)+x(n-N)]+\rho{y(n-N)} \end{align*} \]
依據上面公式非常容易設計出C代碼,這裡將浮點數實現共用,如需定點實現也非常容易,代碼如下:
#include <stdio.h>
#include <math.h>
#include <string.h>
/*長度應為階數+1*/
#define CMF_RANK 20
typedef double E_SAMPLE;
typedef enum _E_CMF_TYPE{
CMF_TYPE_STOP_BANDS,
CMF_TYPE_PASS_BANDS
}E_CMF_TYPE;
/*定義移動平均寄存器歷史狀態*/
typedef struct _t_CMF
{
E_SAMPLE x[CMF_RANK];
E_SAMPLE y[CMF_RANK];
double b;
double r;
E_CMF_TYPE type;
int index;
}t_CMF;
void comb_filter_init(t_CMF * pCmf,double rho,E_CMF_TYPE type)
{
memset(pCmf,0,sizeof(t_CMF));
pCmf->index = CMF_RANK-1;
pCmf->r = rho;
pCmf->type = type;
if(type==CMF_TYPE_STOP_BANDS)
pCmf->b = (1+rho)/2;
else
pCmf->b = (1-rho)/2;
}
E_SAMPLE comb_filter(t_CMF * pCmf,E_SAMPLE xn)
{
E_SAMPLE yn=0;
int n_N;
int i=0;
n_N = pCmf->index;
if(pCmf->type == CMF_TYPE_STOP_BANDS)
{
/*y[n] = bx[n]-bx[n-N]+ry[n-N]*/
yn = pCmf->b*(xn-pCmf->x[n_N])+pCmf->r*pCmf->y[n_N];
}
else
{
/*y[n] = bx[n]+bx[n-N]+ry[n-N]*/
yn = pCmf->b*(xn+pCmf->x[n_N])+pCmf->r*pCmf->y[n_N];
}
/*存儲yn為下次迭代準備*/
pCmf->y[n_N] = yn;
pCmf->x[n_N] = xn;
if(pCmf->index==0)
pCmf->index = CMF_RANK-1;
else
pCmf->index--;
return yn;
}
#define SAMPLE_RATE 1000.0f
#define SAMPLE_SIZE 512
#define PI 3.415926f
int main()
{
E_SAMPLE rawSin[SAMPLE_SIZE];
E_SAMPLE outSin[SAMPLE_SIZE];
t_CMF cmf;
FILE *pFile=fopen("./simulationSin.csv","wt+");
if(pFile==NULL)
{
printf("simulationSin.csv opened failed");
return -1;
}
for(int i=0;i<SAMPLE_SIZE;i++)
{
rawSin[i] = 10*sin(2*PI*25*i/SAMPLE_RATE);//+rand()%10;
rawSin[i] += 10*sin(2*PI*50*i/SAMPLE_RATE);
}
/*初始化*/
comb_filter_init(&cmf,-0.22059817649696845,CMF_TYPE_STOP_BANDS);
/*濾波*/
for(int i=0;i<SAMPLE_SIZE;i++)
{
outSin[i]=comb_filter(&cmf,rawSin[i]);
}
for(int i=0;i<SAMPLE_SIZE;i++)
{
fprintf(pFile,"%f,",rawSin[i]);
}
fprintf(pFile,"\n");
for(int i=0;i<SAMPLE_SIZE;i++)
{
fprintf(pFile,"%f,",outSin[i]);
}
/*初始化*/
comb_filter_init(&cmf,-0.22059817649696845,CMF_TYPE_PASS_BANDS);
/*濾波*/
for(int i=0;i<SAMPLE_SIZE;i++)
{
outSin[i]=comb_filter(&cmf,rawSin[i]);
}
/*存儲數據*/
fprintf(pFile,"\n");
for(int i=0;i<SAMPLE_SIZE;i++)
{
fprintf(pFile,"%f,",outSin[i]);
}
fclose(pFile);
return 0;
}
同樣利用excel,生成波形如下:
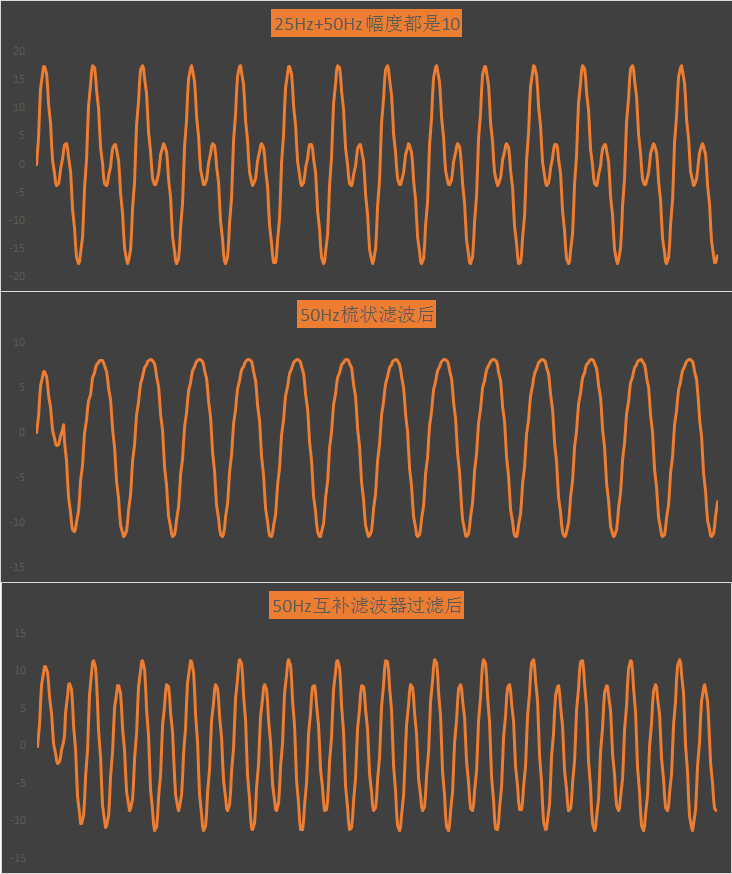
可見,經過梳狀濾波器過濾後,50Hz諧波已經被過濾掉,25Hz 保留下來,而經過其互補濾波器後,25Hz被過濾,其50Hz被保留。如看時域波形不直觀,可利用Python代碼進行FFT展開分析:
梳妝濾波後FFT譜線圖:
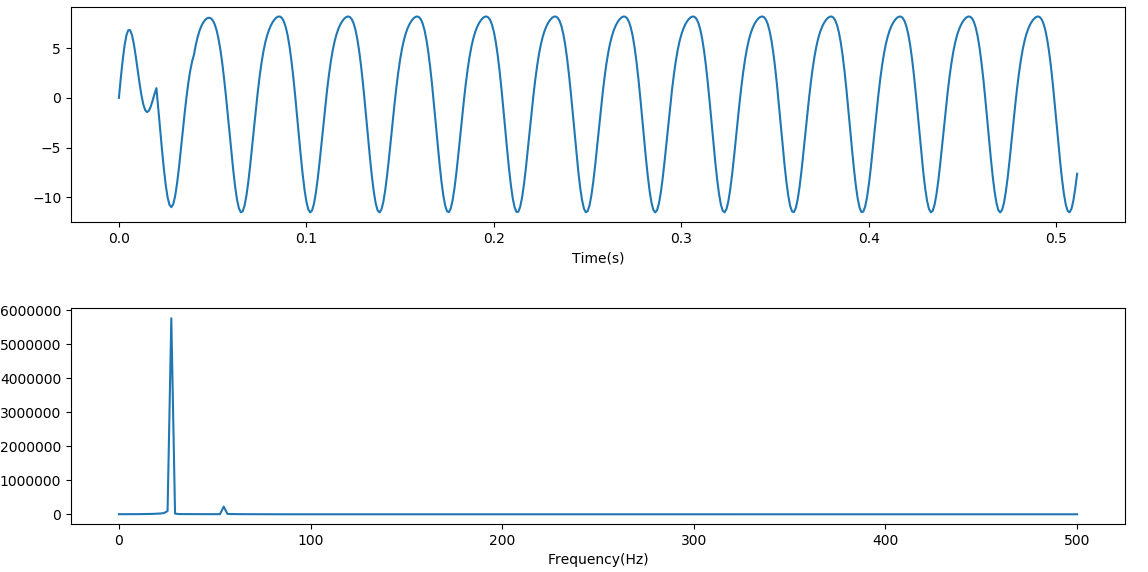
互補梳狀濾波器過濾後FFT譜線圖:
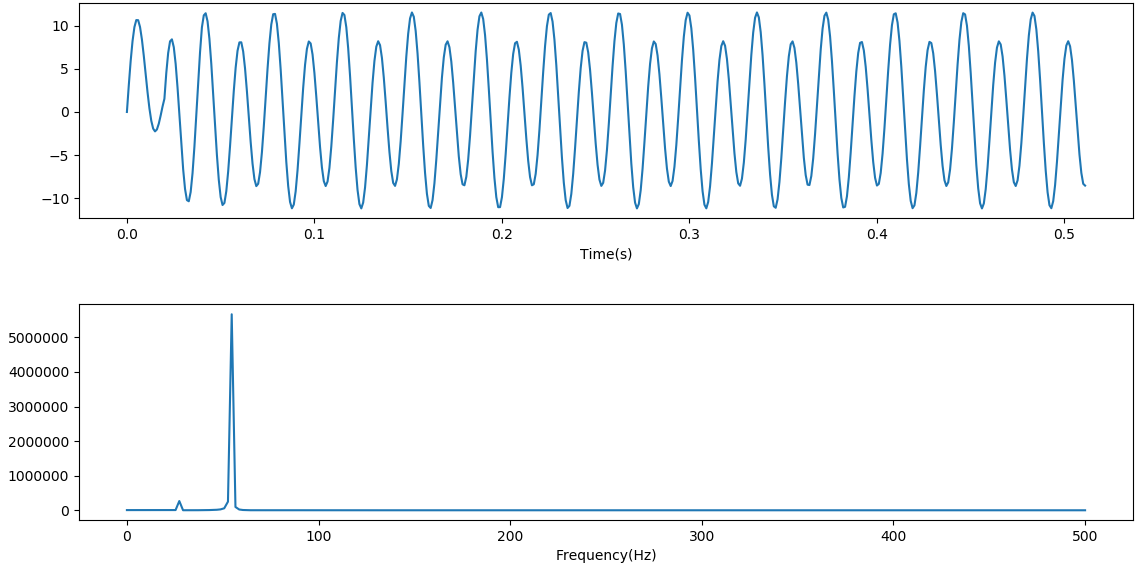
總結:
- 梳妝濾波器本質上是一種IIR濾波器
- 梳妝濾波器在濾除諧波上,利用極小代價就可以比較好的濾除諧波干擾
- 其互補濾波器在時域時會失真,使用時需要考慮
- 如需要考慮計算效率,可以考慮定點優化,但精度會下降。
- 梳妝濾波器在2D/3D圖像處理廣為應用,如有興趣可深入研究
文章出自微信公眾號:嵌入式客棧,更多內容,請關註本人公眾號,嚴禁商業使用,違法必究




