【導讀】：前面的文章介紹了移動平均濾波器、IIR濾波器、梳狀濾波器，今天來談談FIR濾波器的設計實現。

本篇文章依然採用4W1H進行描述，從What Why Where When How幾個維度展開。為了便於理解4W1H，依然把5W1H的圖附上。

FIR濾波器之What？

LTI線性時不變系統衝激響應按照其是有限長還是無限長可分為FIR(Finite Impulse Response)有限長衝激響應系統以及無限長衝激響應IIR(Infinite Impulse Response)系統。FIR是全零點系統，也即Z傳遞函數在Z復平面極點全在Z=0處。至於這些概念是如何得來的，不是本文重點，如果有興趣深究，可以查閱數字信號處理方面的書籍。

\[H(Z)=\sum_{i=0}^{N-1}h(n)Z^{-n} \]

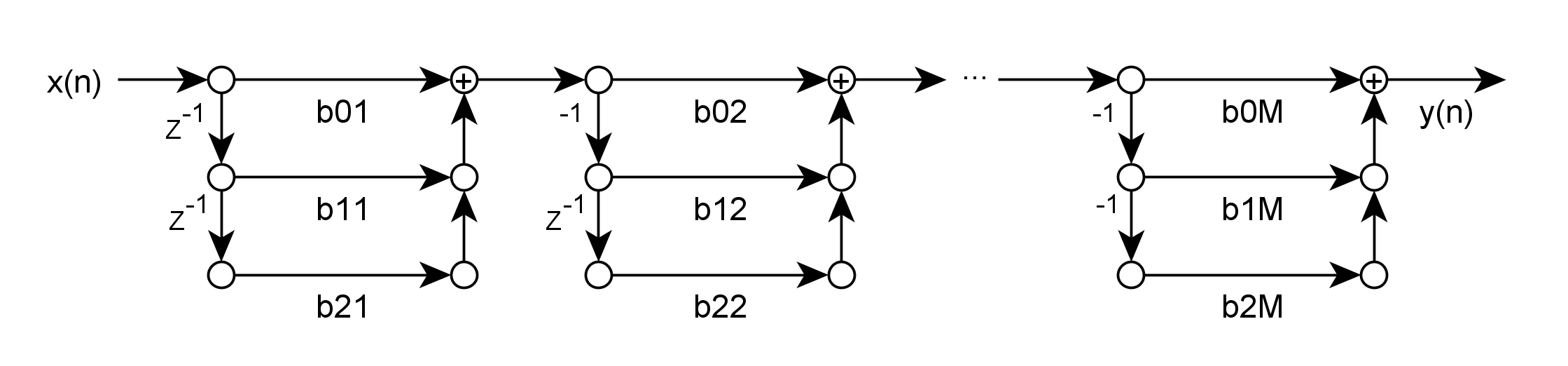
FIR濾波器具有多種實現形式，比如直接型、二階級聯型、Lattice結構，都只是上述基本傳遞函數的不同數學表達形式，沒有本質區別，只是在具體演算法實現上各具特點。這裡將二階級聯形式描述如下。

二階級聯的意思是將上述傳遞函數分解為二階多項式塊連乘的形式，其數學表達如下：

\[H(Z)=\prod_{k=0}^M(b_{0k}+b_{1k}Z^{-1}+b_{2k}Z^{-2}) \]

FIR濾波器之Why？

為啥稱前面的傳遞函數形式的系統為有限長衝激響應呢？要從概念上理解，首先須從衝激響應說起，什麼是系統的衝激響應？系統在單位衝激函數激勵下引起的零狀態響應被稱之為該系統的“衝激響應”。

那麼什麼又是是衝激函數呢？

單位衝激函數（Unit-Impulse Function）是信號與系統學科中的一個重要概念。它是一個面積等於1的理想化了的窄脈衝。也就是說，這個脈衝的幅度等於它的寬度的倒數。當這個脈衝的寬度愈來愈小時，它的幅度就愈來愈大。當它的寬度按照數學上極限法則趨近於零時，那麼它的幅度就趨近於無限大，這樣的一個脈衝就是“單位衝激函數”。在實際工程中，像“單位衝激函數”這樣的信號是不存在的，至多也就是近似而已。在理論上定義這樣一個函數，完全是為了分析研究方便的需要。<百度百科>

單位衝激函數又稱為狄拉克函數，定義為：

• 當\(t\neq{0}\)時, \(\delta(t)=0\)
• \(\int_{{-}\infty}^{\infty}\delta(t)dt=1\)

這玩意純數學表達僅為從嚴謹角度出發，卻不易懂，在數字信號處理領域或者稱為離散系統領域，定義單位衝激（也有的稱為單位採樣/單位函數/單位脈衝，管它張三、李四）這裡只需要明白其物理含義即可：

\[\delta(n)=\begin{cases} 1, (n=0) \\ 0, (n\neq0) \end{cases} \]

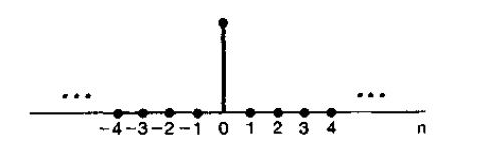
那麼所謂單位衝激函數響應，就是一個系統輸入這樣一個能量激勵，在輸出端所觀測到的響應信號，那麼對於FIR系統而言，其響應在經過有限長的序列後，最後將穩定在0，這就是有限長衝激響應的內涵，而無限長則是有這樣一個衝激激勵後，其響應經過無限長序列後仍不會穩定到0。再進一步思考，為什麼呢？因為FIR系統輸出不會反饋回輸入端，則保證其輸出響應是有限長序列， 因此，“有限衝激響應”幾乎與“無反饋”等價。但是，如果採用反饋，但脈衝響應是有限的，則濾波器仍然是FIR。 一個示例是移動平均濾波器，其中每次有新採樣進入時都會減去（反饋）第N個先前的採樣。即使使用反饋，該濾波器也具有有限的脈衝響應：在N個採樣樣本之後，輸出 將始終為零。IIR濾波器使用反饋，因此，當輸入脈衝時，理論上輸出會無限地振蕩。所以對於這兩個概念的區分從字面去理解即可。

在實踐中，即使是IIR系統，其脈衝響應也通常接近零，並且可以忽略不計。但是，引起IIR或FIR響應的物理系統是不同的，這就是區別的重要性。例如，由電阻器，電容器和/或電感器（也許還有線性放大器）組成的模擬電子濾波器通常是IIR濾波器。另一方面，基於不使用反饋的抽頭延遲線的離散時間濾波器（通常是數字濾波器）必然是FIR濾波器。模擬濾波器中的電容器（或電感器）具有“記憶特性也即儲能特性”，並且其內部狀態不會因脈衝而完全放鬆。但是在後一種情況下，在脈衝到達抽頭延遲線的末端之後，系統不再對該脈衝進行存儲，並返回到其初始狀態。超出該點的脈衝響應恰好為零。多說一句，在使用IIR時，是否穩定包括在模擬電路設計時，需要考慮的一個重要指標就是其系統的相位裕度的概念。有興趣的可以去研究一下。

FIR濾波器之Where？

FIR濾波器的應用領域非常的廣泛：

• 音頻信號處理領域，會在信號處理層大量運用FIR濾波器進行信號濾波
• Sigma-Delta ADC晶元內部就利用數字邏輯電路實現了FIR濾波器
• 涉及到採集信號的儀器儀錶領域廣為應用
• 系統辨識領域，對於系統建模也常常採用濾波器濾除採集信號，以消除雜訊提高建模的準確性
• 圖像處理領域也廣為應用
• ......

說了這麼多，就是想說這個東東非常有用，個人認為這是電子類開發工程師進階神器，值得深入研究，反覆探究，這也是為什麼花這麼多精力寫這個系列的初心，希望自己的一些經驗你能幫助到其他的人。所以如果你沒有這方面的經驗，剛好看到這系列的文章，還請幫忙轉發分享以幫助到更多的人，哈哈哈。當然如果您是這方面的行家裡手如果發現文中有錯誤或者需要改進的地方，也真誠的期待能告訴與我，幫助我糾正錯誤。所以導讀中所說懇請指正，絕非套話。

FIR濾波器之When？

當實現感測器時，個人建議首先理清楚信號鏈模型，信號的頻域帶寬，是否有潛在混入雜訊的可能。是故個人認為：

• 如果在硬體電路處理後任然有雜訊，此時就可以考慮採用濾波器，如果所用晶元算力不錯，就可以考慮採用FIR濾波器
• 如果在硬體也能實現有源濾波器能解決產品中的雜訊干擾，但是發現硬體的方法需要成本比較高，或者PCB面積受限時，也推薦考慮採用數字濾波器實現。因為往往有源濾波器要實現一個比較好的通頻帶高Q值時，其階數往往很高，而且可能需要一些特殊規格的電阻電容實現所需的頻帶，此時數字濾波器僅需要一段代碼搞定，而且效果往往比硬體濾波器更好也更靈活。
• 如果在系統中發現採用IIR拓撲類型濾波器無法滿足線性相位需求，或者發現使用IIR濾波器，濾波器輸出出現嚴重失真或者不穩定現象時，推薦考慮採用FIR濾波器。
• 再比如你是用FPGA設計一個系統，也需要實現模擬信號採集，此時也可以考慮直接用數字電路直接實現FIR濾波器，因為FPGA的硬並行特性為實現高階FIR濾波器提供了非常好硬體基礎。
• ......

FIR濾波器之How？

設計FIR濾波器從書本知識，可以發現有窗函數法、切比雪夫逼近法、最小均方差等方法，這些方法從數學理論上給出了設計原理，但作為工程師而言，個人認為只需要理解其概念內涵即可。學以致用才是目的，所以強大的MATLAB 工具fdatool以及實現了這些基本的設計方法。當然如果對於MATLAB函數很熟悉，直接來段MATLAB程式效果也是一樣的。這裡仍然利用fdatool來示例如何設計實現FIR濾波器。

本文以實現採樣頻率48kHz，帶寬為100Hz～10KHz帶通濾波器，假定是一個麥克風語音採集系統，人的發聲頻率在100Hz(男低音)到10000Hz(女高音)範圍內。

假設設計一個512階的FIR帶通濾波器，其指標為：

• Fstop1為60Hz, Fpass1為100Hz
• Fpass2為10000Hz, Fstop2為10200Hz
• Wstop1 為40dB,Wstop2 為40dB,

其幅頻響應為：

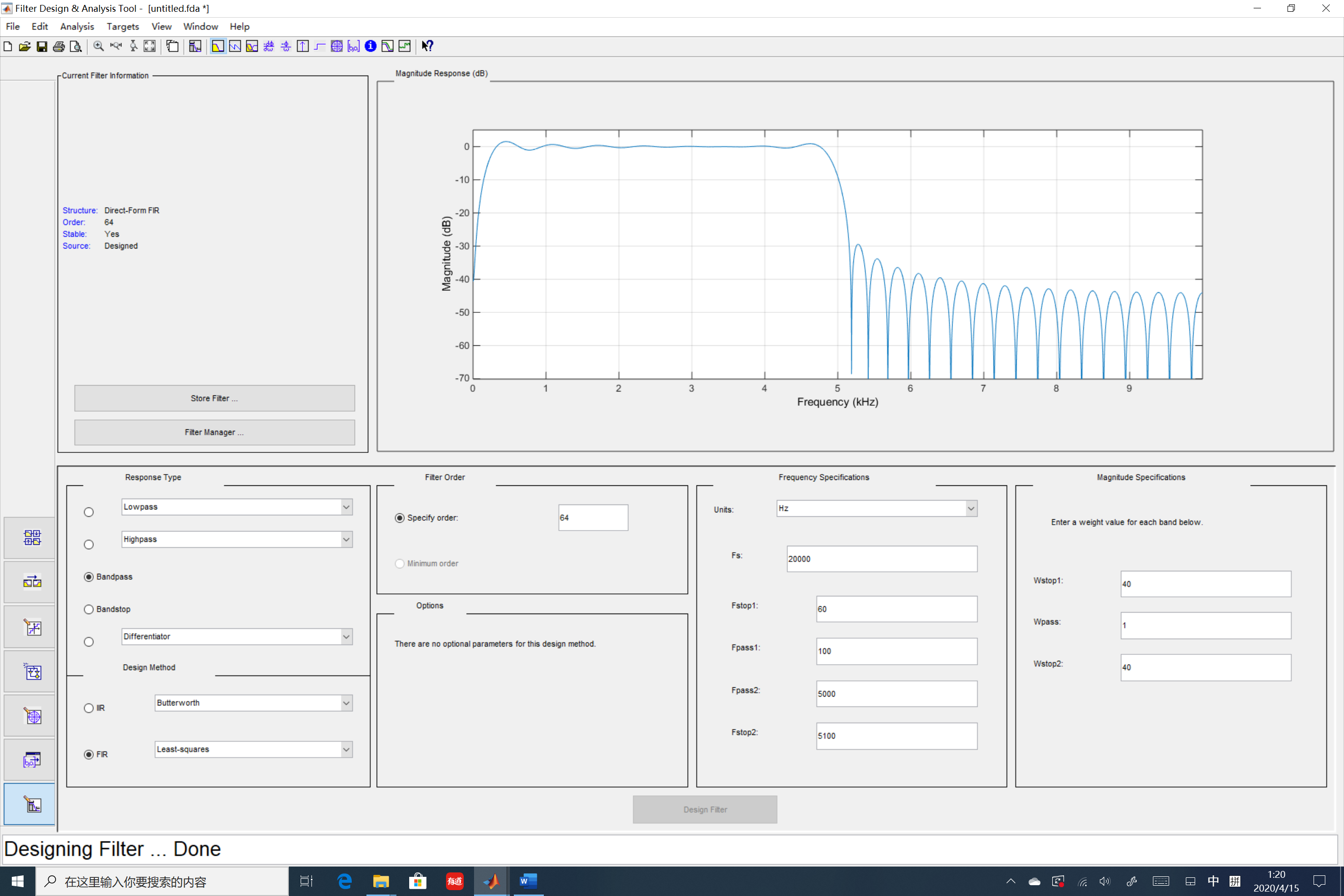
相頻響應如下圖，可見在通頻帶內，隨頻率的增加，其相位延遲也是線性增加的，這就是線性相位的含義。

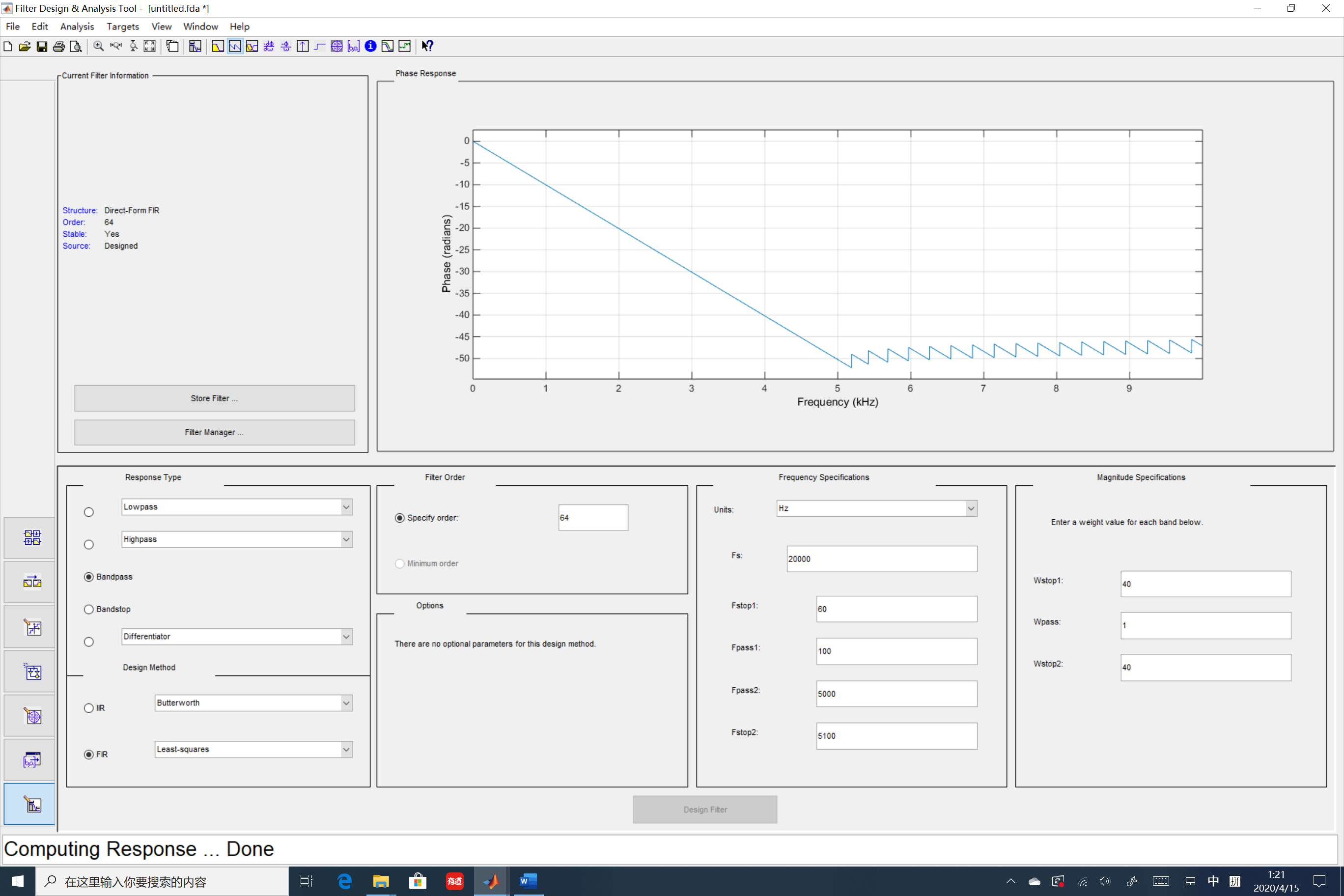
前面說到衝激響應，這裡將圖附上幫助理解。

其參數太長就不貼在這裡了，直接放到測試代碼中。

接下來就進行C代碼實現，由其Z傳遞函數，比較容易得到其差分方程為：

\[y[n]=\sum_{i=0}^{N}h_ix[n-i] \]

C語言實現及測試程式如下：

#include <stdio.h>
#include <math.h>
#include <string.h>

/*長度應為階數+1*/
#define FIR_RANK  64
typedef float E_SAMPLE;
typedef float E_COEFF;

/*定義移動平均寄存器歷史狀態*/
typedef struct _t_FIR_STATE
{
    E_SAMPLE x[FIR_RANK];
    int index;
}t_FIR_STATE;
typedef struct _t_FIR_COFF
{
    E_COEFF coeff[FIR_RANK+1];
}t_FIR_COFF;

void fir_init(t_FIR_STATE * pFir)
{
    memset(pFir,0,sizeof(t_FIR_STATE));
    pFir->index = -1;
}

E_SAMPLE fir_filter(t_FIR_STATE * pFir,const t_FIR_COFF *pCff,E_SAMPLE xn)
{
    double yn=0;
    int i=0;
    if(pFir->index==-1)
    {
        for(i=0;i<FIR_RANK;i++)
        {
            pFir->x[i] = xn;
        }
        pFir->index = FIR_RANK-1;
    }

    //if(pCmf->index<FIR_RANK-1)
    yn = pCff->coeff[0]*xn;
    for(i=pFir->index+1;i<FIR_RANK;i++)
    {
        yn += pCff->coeff[i-pFir->index]*pFir->x[i];
    }

    for(i=0;i<=pFir->index;i++)
    {
        yn += pCff->coeff[FIR_RANK+i-pFir->index]*pFir->x[i];
    }

    /*存儲yn為下次迭代準備*/
    pFir->x[pFir->index] = xn;


    if(pFir->index==0)
        pFir->index = FIR_RANK-1;
    else
        pFir->index--;

    return yn;
}

#define SAMPLE_RATE 20000.0f
#define SAMPLE_SIZE 1024
#define PI 3.415926f
const t_FIR_COFF coff={
-0.011262440038163873,-0.013943401141922421,-0.0081737662228137248,-0.0098154763556324871,
-0.02113385595071398,-0.02217110374674186, -0.0086760432252453272,-0.0053777731960091618,
-0.020684485378668873,-0.026487927162555332,-0.0099598536658154907,-0.0020760557762302574,
-0.020234665687863043,-0.030631983578413714,-0.010974822973539177, 0.0018520388094555051,
-0.019945227624679929,-0.035904990372740073,-0.011725945979530706, 0.0077957069084101244,
-0.019771168997491595,-0.044197538806107613,-0.012256200606615813, 0.018808015681099421,
-0.01967177670413162, -0.06116090480347313, -0.012595538855093001, 0.047238864700837428,
-0.019621294906038051,-0.12211186053365741,-0.012761289558492961, 0.30206303190057837,
 0.4803940881892042,   0.30206303190057837,-0.012761289558492961,-0.12211186053365741,
-0.019621294906038051, 0.047238864700837428,-0.012595538855093001,-0.06116090480347313,
-0.01967177670413162,  0.018808015681099421,-0.012256200606615813,-0.044197538806107613,
-0.019771168997491595, 0.0077957069084101244,-0.011725945979530706,-0.035904990372740073,
-0.019945227624679929, 0.0018520388094555051,-0.010974822973539177,-0.030631983578413714,
-0.020234665687863043,-0.0020760557762302574,-0.0099598536658154907,-0.026487927162555332,
-0.020684485378668873,-0.0053777731960091618,-0.0086760432252453272,-0.02217110374674186,
-0.02113385595071398, -0.0098154763556324871,-0.0081737662228137248,-0.013943401141922421,
-0.011262440038163873
};
int main()
{
    E_SAMPLE rawSin[SAMPLE_SIZE];
    E_SAMPLE outSin[SAMPLE_SIZE];

    t_FIR_STATE fir;

    FILE *pFile=fopen("./simulationSin.csv","wt+");
    if(pFile==NULL)
    {
        printf("simulationSin.csv opened failed");
        return -1;
    }

    for(int i=0;i<SAMPLE_SIZE;i++)
    {
        rawSin[i]  = 5*sin(2*PI*20*i/SAMPLE_RATE);//+rand()%10;
        rawSin[i] += 5*sin(2*PI*7000*i/SAMPLE_RATE);
        rawSin[i] += 10*sin(2*PI*2500*i/SAMPLE_RATE);
    }

    /*初始化*/
    fir_init(&fir);
    /*濾波*/
    for(int i=0;i<SAMPLE_SIZE;i++)
    {
        outSin[i]=fir_filter(&fir,&coff,rawSin[i]);
    }

    for(int i=0;i<SAMPLE_SIZE;i++)
    {
        fprintf(pFile,"%f,",rawSin[i]);
    }

    fprintf(pFile,"\n");
    for(int i=0;i<SAMPLE_SIZE;i++)
    {
        fprintf(pFile,"%f,",outSin[i]);
    }

    fclose(pFile);

    return 0;
}

同樣利用excel生成波形：

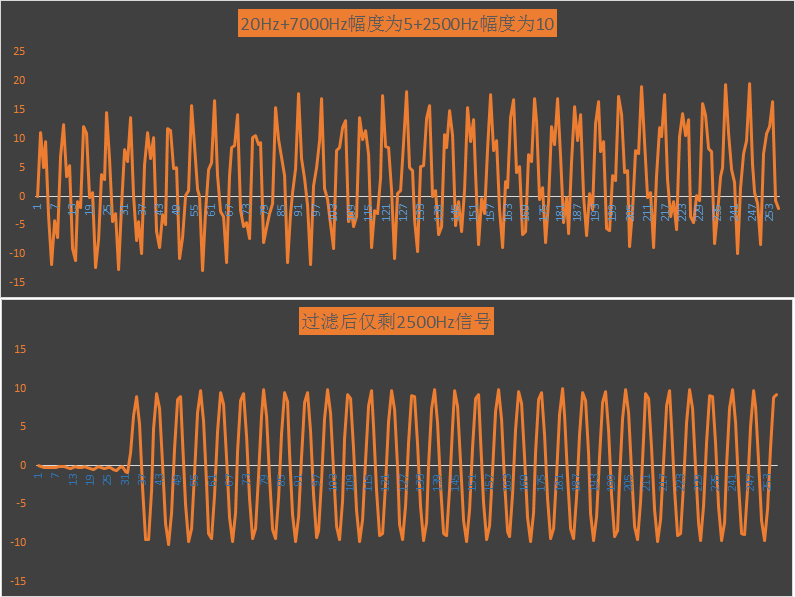
可見濾波效果不錯。下麵進行總結：

FIR濾波器與IIR濾波器相比的優勢：

• 可以很容易地將它們設計為“線性相位”（通常是）。簡而言之，線性相位濾波器會延遲輸入信號，但不會使其相位失真。
• 很容易實現。在大多數DSP微處理器上，可以通過迴圈一條指令來完成FIR計算。
• 適合於多速率應用。所謂多速率，是指“抽取”（降低採樣率），“內插”（提高採樣率）或兩者兼而有之。有興趣的可進一步深入研究，無論是抽取還是插值，FIR濾波器的使用都可以省略某些計算，從而提供了重要的計算效率。相反，如果使用IIR濾波器，則即使要丟棄每個輸出，每個輸出也必須單獨計算。
• 具有令人滿意的數值屬性。實際上，大部分DSP濾波器都必須使用有限精度演算法（即有限的定點位數）來實現。由於使用了反饋，因此在IIR濾波器中使用有限精度算術會引起嚴重的誤差問題，但是沒有反饋的FIR濾波器通常可以使用更少的位來實現，並且設計人員需要解決的與非理想算術有關的實際問題也更少。
• 可以使用分數演算法來實現。與IIR濾波器不同，始終可以使用幅度小於1.0的繫數來實現FIR濾波器。 （如果需要，可以在FIR濾波器的輸出處調整其總增益。）使用定點DSP時，這是一個重要的考慮因素，因為它使實現更加簡單。

FIR濾波器與IIR濾波器相比的劣勢：

• 需要更多的記憶體和/或計算才能實現給定的濾波器響應特性。 而且，某些響應對於用FIR濾波器不易實現，因為階數太高。

另外如果使用的晶元具有乘累加指令，則非常利於實現FIR濾波器。

文章出自微信公眾號：嵌入式客棧，更多內容，請關註本人公眾號,嚴禁商業使用，違法必究