歸併排序 歸併排序演算法的核心就是 “歸併”,將兩個有序的數列合併,形成更大的有序數組。 歸併排序的原理 上面說了,歸併排序的核心就是“歸併”。如果排序一個數組,那麼將數組從中間分成前後兩部分,對前後兩部分分別進行排序,然後再將排序好的合併在一起,那麼這樣整個數組就會成為更大的有序數組。例如下麵示圖: ...
歸併排序
歸併排序演算法的核心就是 “歸併”,將兩個有序的數列合併,形成更大的有序數組。
歸併排序的原理
上面說了,歸併排序的核心就是“歸併”。如果排序一個數組,那麼將數組從中間分成前後兩部分,對前後兩部分分別進行排序,然後再將排序好的合併在一起,那麼這樣整個數組就會成為更大的有序數組。例如下麵示圖:
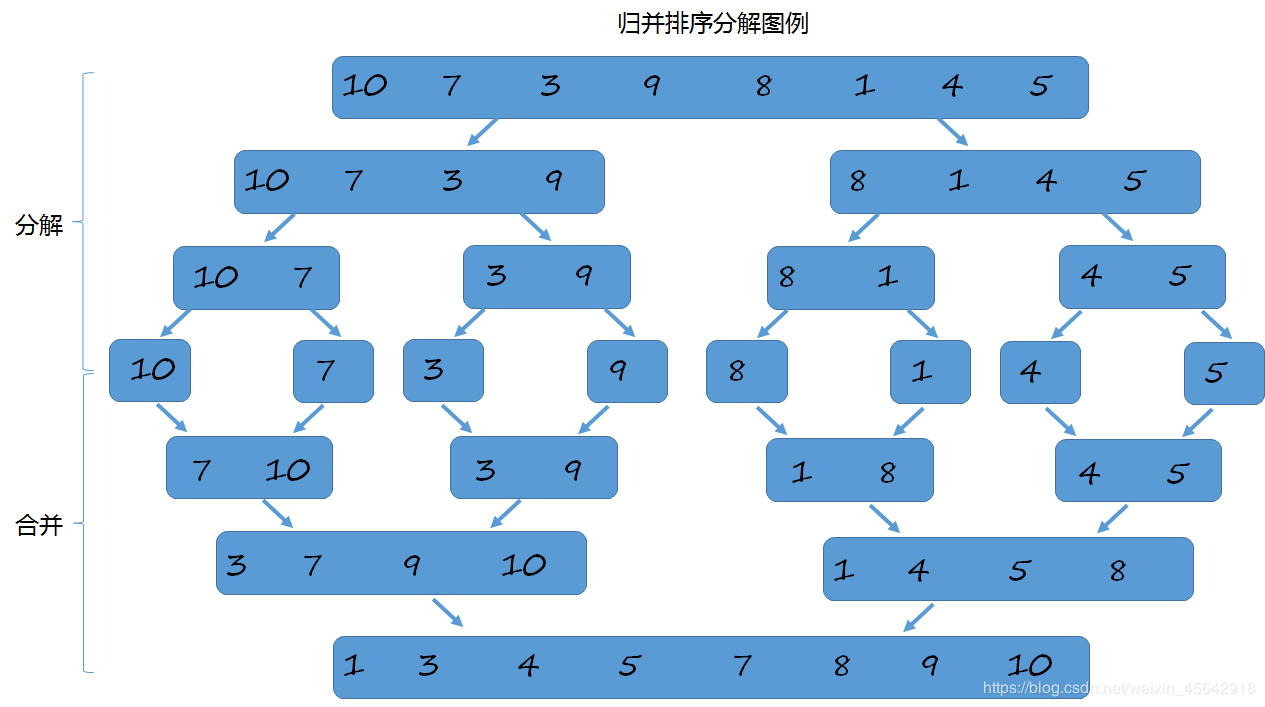
歸併排序使用的思想是分治思想,即是分而治之。將複雜問題分解成兩個或者多個規模相同或類似的子問題,然後繼續細化,當子問題足夠簡單,能夠被求解,那麼複雜的問題也就能夠被求解出來。
這裡跟遞歸的思想很像。遞歸也是將大問題細化為小問題,找出終止條件和遞推公式。分治演算法一般都是用遞歸實現的。分治的思想是一種解決問題的處理思想,遞歸是一種編程技巧,兩者不會衝突。
上面說了,歸併排序能夠使用遞歸實現,那麼現在先寫出遞推公式和終止條件。
# 遞推公式
merge_sort(a...b) = merge(merge_sort(a...k), merge_sort(k+1, b))
# 終止條件
a >= b,不再繼續分解
這裡解釋下上面的公式,終止條件不細講,這裡表示的,索引 a 大於等於 索引 b,即是已經到達數組末尾,不能夠再細分。
講下遞推公式,merge_sort(a...b),表示給索引 a 到 k 之間的數組進行排序。這裡將分體轉為為兩個子問題,merge_sort(a...k) 和 merge_sort(k+1...b),其中 k 表示原數組中間的位置。而 merge() 函數表示當兩個將兩個排好序的子數組合併,這樣就能夠使原數組實現排序。
現在將這個遞推公式轉化為代碼(這裡使用偽代碼):
# nums 表示數組,a 為起始點,b 為數組末尾索引
def merge_sort(nums, a, b):
# 終止條件
if a >= b:
return
# 取中間位置
k = (a + b) // 2
# 分治遞歸
merge_sort(nums, a, k)
merge_sort(nums, k+1, b)
merge(nums[a...b], nums[a...k], nums[k+1, b])
最後 merge() 函數的作用,就是將後面兩個子數組合併好後放到 nums[a...b] 中。現在主要的問題是如何實現分解後排序合併?
先用一個簡單的示例,如下示圖:

先申請臨時數組 temp,定義指針 i,j 分別指向 兩個子數組的第一個元素。比較 nums[i],nums[j],較小的元素放入臨時數組中,同時該元素的指針向右移動。
迴圈上面的過程,直到其中一個子數組的所有數據都放入臨時數組中,這個時候,將另外一個數組剩下的部分也放到臨時數組中。這個臨時數組就是最終合併的結果,將其複製回原數組即可。
現在用偽代碼實現這個過程:
def merge(nums[a...b], nums[a...k], nums[k+1, b]):
# length 表示數組大小
temp = [0] * length
# 初始化指針,i, j, ti
i, j, ti, = a, k+1, 0
# 取小值放入臨時數組中,
while (i <= k and j <= b):
if (nums[i]<=nums[j]):
temp[ti]=nums[i]
i+=1
else:
temp[ti]=nums[j]
j+=1
ti+=1
# 合併時會出現一個數組全部放入臨時數組中,
# 另外一個數組還有剩餘,這裡將剩餘部分也放到臨時數組中
if i < nums[a...k].length:
for x in range(i, nums[a...k].length):
temp[ti] = nums[x]
ti += 1
else:
for x in range(j, nums[k+1...b].length):
temp[ti] = nums[x]
ti += 1
# 如果需要複製回原數組,也可以直接複製
return temp
以上本篇幅就是關於歸併排序的主要內容。
歡迎關註微信公眾號《書所集錄》



