我的LeetCode：https://leetcode-cn.com/u/ituring/

我的LeetCode刷題源碼[GitHub]：https://github.com/izhoujie/Algorithmcii

LeetCode 1162. 地圖分析

題目

你現在手裡有一份大小為 N x N 的『地圖』（網格） grid，上面的每個『區域』（單元格）都用 0 和 1 標記好了。其中 0 代表海洋，1 代表陸地，你知道距離陸地區域最遠的海洋區域是是哪一個嗎？請返回該海洋區域到離它最近的陸地區域的距離。

我們這裡說的距離是『曼哈頓距離』（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 這兩個區域之間的距離是 |x0 - x1| + |y0 - y1| 。

如果我們的地圖上只有陸地或者海洋，請返回 -1。

示例 1：

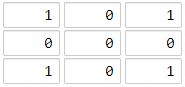
輸入：[[1,0,1],[0,0,0],[1,0,1]]
輸出：2
解釋： 
海洋區域 (1, 1) 和所有陸地區域之間的距離都達到最大，最大距離為 2。

示例 2：

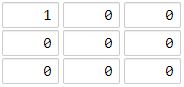
輸入：[[1,0,0],[0,0,0],[0,0,0]]
輸出：4
解釋： 
海洋區域 (2, 2) 和所有陸地區域之間的距離都達到最大，最大距離為 4。

提示：

• 1 <= grid.length == grid[0].length <= 100
• grid[i][j] 不是 0 就是 1

來源：力扣（LeetCode）
鏈接：https://leetcode-cn.com/problems/as-far-from-land-as-possible
著作權歸領扣網路所有。商業轉載請聯繫官方授權，非商業轉載請註明出處。

解題思路

首先能讀懂題意我覺得就已經算很厲害了...至少我一開始看了半天沒看懂 - -||
對於此類題首先的想法是BFS、DFS之類的，此題確實用BFS、DFS都可以解決，BFS更易理解好懂些，
此外還有個動態規劃的解法，不易理解，但是代碼更簡潔且效率最高；

思路1-BFS

步驟：

1. 使用優先隊列，先對所有的陸地（1）入隊；
2. while處理優先隊列，遇到海洋（0）的將陸地值+1覆蓋到海洋並將其入隊；
3. 至while迴圈完，最後一個處理的海洋塊即為最遠距離，取其數組值-1即可；

BFS:比較形象的理解就是水圈，農村包圍城市的意思
DFB:關公溫酒斬華雄、千里走單騎，我自己對DFS的形象記憶

思路2-dp動態規劃

1-先左上角到右下角遍歷；
2-再右下角到左上角的遍歷；

詳解：待補充...

演算法源碼示例

package leetcode;

import java.util.ArrayDeque;

/**
 * @author ZhouJie
 * @date 2020年3月29日 下午9:45:11 
 * @Description: 1162. 地圖分析
 *
 */
public class LeetCode_1162 {

}

class Solution_1162 {

	/**
	 * @author: ZhouJie
	 * @date: 2020年3月29日 下午11:31:43 
	 * @param: @param grid
	 * @param: @return
	 * @return: int
	 * @Description: 1-BFS，所有陸地作為初始點，開始擴散，使用優先隊列；
	 *
	 */
	public int maxDistance_1(int[][] grid) {
		ArrayDeque<int[]> deque = new ArrayDeque<int[]>();
		int m = grid.length;
		int n = grid[0].length;
		for (int i = 0; i < m; i++) {
			for (int j = 0; j < n; j++) {
				if (grid[i][j] == 1) {
					deque.offer(new int[] { i, j });
				}
			}
		}

		int[] last = null;
		boolean noSea = true;
		// 四個搜索方向
		int[] dx = new int[] { 1, -1, 0, 0 };
		int[] dy = new int[] { 0, 0, 1, -1 };
		while (!deque.isEmpty()) {
			last = deque.poll();
			int x0 = last[0];
			int y0 = last[1];
			for (int i = 0; i < 4; i++) {
				int x = x0 + dx[i];
				int y = y0 + dy[i];
				if (x < 0 || x >= m || y < 0 || y >= n || grid[x][y] != 0) {
					continue;
				}
				grid[x][y] = grid[x0][y0] + 1;
				noSea = false;
				deque.offer(new int[] { x, y });
			}
		}
		return noSea || last == null ? -1 : grid[last[0]][last[1]] - 1;
	}

	/**
	 * @author: ZhouJie
	 * @date: 2020年3月29日 下午11:31:40 
	 * @param: @param grid
	 * @param: @return
	 * @return: int
	 * @Description: 2-動態規劃，基於曼哈頓距離的概念，即距離總是為正上方和左前方的距離和或正下方和右前方的距離和，
	 *				對grid進行兩次dp，一次從左上角到右下角，一次從右下角到左上角；
	 *
	 */
	public int maxDistance_2(int[][] grid) {
		int m = grid.length;
		int n = grid[0].length;
		boolean noLand = true;
		// 從左上角到右下角的dp，順帶標記noLand
		for (int i = 0; i < m; i++) {
			for (int j = 0; j < n; j++) {
				if (grid[i][j] == 1) {
					noLand = false;
					continue;
				}
				if (grid[i][j] == 0) {
					grid[i][j] = m + n;
				}
				if (i > 0) {
					grid[i][j] = Math.min(grid[i][j], grid[i - 1][j] + 1);
				}
				if (j > 0) {
					grid[i][j] = Math.min(grid[i][j], grid[i][j - 1] + 1);
				}
			}
		}
		int distance = 0;
		// 右下方到左上方的dp，計算distance
		for (int i = m - 1; i > -1; i--) {
			for (int j = n - 1; j > -1; j--) {
				if (grid[i][j] != 1) {
					if (i < m - 1) {
						grid[i][j] = Math.min(grid[i][j], grid[i + 1][j] + 1);
					}
					if (j < n - 1) {
						grid[i][j] = Math.min(grid[i][j], grid[i][j + 1] + 1);
					}
					distance = Math.max(distance, grid[i][j]);
				}
			}
		}
		return noLand ? -1 : --distance;
	}
}