什麼是線性回歸(Linear Regression) 我們在初中可能就接觸過,y=ax,x為自變數,y為因變數,a為繫數也是斜率。如果我們知道了a繫數,那麼給我一個x,我就能得到一個y,由此可以很好地為未知的x值預測相應的y值。在只有一個變數的情況下,線性回歸可以用方程:y = ax+b 表示;多元 ...
什麼是線性回歸(Linear Regression)
我們在初中可能就接觸過,y=ax,x為自變數,y為因變數,a為繫數也是斜率。如果我們知道了a繫數,那麼給我一個x,我就能得到一個y,由此可以很好地為未知的x值預測相應的y值。在只有一個變數的情況下,線性回歸可以用方程:y = ax+b 表示;多元線性回歸方程可以表示為:y = a0 + a1*x1 + a2*x2 + a3*x3 + ...... +an*xn。
機器學習的實質說白了就是通過數據之間的關係找出某種映射f:X→y。而針對線性回歸來說就是假定X與y之間有線性相關關係。回歸模型就是表示從輸入變數到輸出變數之間映射的函數,回歸問題的學習等價於函數擬合:選擇一條函數曲線使其很好地擬合已知數據且很好地預測未知數據。
線性回歸的表示是一個方程,它描述了一條線,通過尋找輸入變數繫數(B)的特定權重,擬合輸入變數(x)和輸出變數(y)之間的關係。
 例如:y=B0+B1∗x,我們將在給定輸入x的情況下預測y,線性回歸學習演算法的目標是找到繫數B0和B1的值。 可以使用不同的技術從數據中學習線性回歸模型,如普通最小二乘的線性代數解和梯度下降優化。
例如:y=B0+B1∗x,我們將在給定輸入x的情況下預測y,線性回歸學習演算法的目標是找到繫數B0和B1的值。 可以使用不同的技術從數據中學習線性回歸模型,如普通最小二乘的線性代數解和梯度下降優化。
線性回歸的模型函數
回歸分析中,只包括一個自變數和一個因變數,且二者的關係可用一條直線近似表示,這種回歸分析稱為一元線性回歸分析。如果回歸分析中包括兩個或兩個以上的自變數,且因變數和自變數之間是線性關係,則稱為多元線性回歸分析。多元線性回歸模型如下(n=1,表示的是一元一次方程):
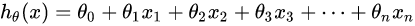
預設x0總是等於1,表達式也可以寫成:
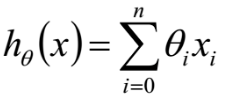
進一步用矩陣形式表達更加簡潔如下:
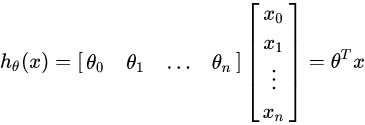
再簡化得: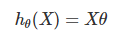
其中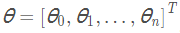 ,
,  ,
, 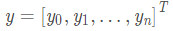 。
。
線性回歸的損失函數
得到了模型,我們要根據已知數據集,在假設空間中,選出最合適的線性回歸模型。這時,就要引出損失函數。即找出使損失函數最小的向量θ。線性回歸的目的就是求解出合適的θ。損失函數(有時也被成為代價函數):是用來估量你模型的預測值 f(x)與真實值 Y的不一致程度,損失函數越小,模型的效果就越好。線性回歸中,損失函數用均方誤差表示,因此損失函數就是我們尋找最佳模型的一種依據。線上性回歸這裡,對應的就是找出最符合數據的權重參數 θ→,即[θ0,θ1,...,θn]T。一般線性回歸我們用均方誤差(MSN)作為損失函數。損失函數的代數法表示如下:
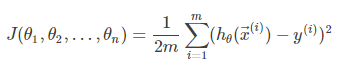
我們並不關係損失函數的最小值是多少,而僅僅關心損失函數最小時的模型參數的值即可,也可寫成如下所示(公式里的1/2對損失函數沒有影響,只是為了能抵消求導後的乘數2):
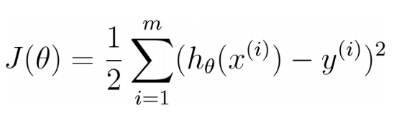
進一步用矩陣形式表達損失函數:

由於矩陣法表達比較的簡潔,後面我們將統一採用矩陣方式表達模型函數和損失函數。
線性回歸中,損失函數用均方誤差表示的證明過程,可以看博客 https://zhuanlan.zhihu.com/p/48205156 的 "線性回歸的損失函數" 部分介紹。
線性回歸的演算法
現在,我們的目標就成了求解向量θ使得J(θ)最小。我們常用的有兩種方法來求損失函數最小化時候的θ參數:一種是梯度下降法,一種是最小二乘法。梯度下降法,是搜索演算法,先給 θ 賦個初值,然後再根據使 J(θ) 更小的原則對 θ 進行修改,直到最小 θ 收斂,J(θ) 達到最小,也就是不斷嘗試;另外一種是正規方程法,要使 J(θ) 最小,就對 θ 求導,使導數等於 0,求得 θ。
如果採用梯度下降法,則θ的迭代公式是這樣的:
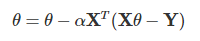
通過若幹次迭代後,我們可以得到最終的θθ的結果
如果採用最小二乘法,則θ的結果公式如下:
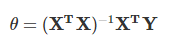
梯度下降法的演算法可以有代數法和矩陣法(也稱向量法)兩種表示,同樣最小二乘法也有矩陣法和代數法兩種表示。詳細證明過程可以參考下麵兩篇博客內容:https://www.cnblogs.com/pinard/p/5976811.html
https://www.cnblogs.com/pinard/p/5970503.html
最小二乘法 vs 梯度下降法:
通過上面推導,我們不難看出,二者都對損失函數的回歸繫數進行了求偏導,並且所得到的推導結果是相同的,那麼究竟哪裡不同呢?如果仔細觀察,可以觀察到:最小二乘法通過使推導結果等於0,從而直接求得極值,而梯度下降則是將推導結果帶入迭代公式中,一步一步地得到最終結果。簡單地說,最小二乘法是一步到位的,而梯度下降是一步步進行的。因而通過以上的異同點,總結如下:
最小二乘法:
- 得到的是全局最優解,因為一步到位,直接求極值,因而步驟簡單
- 線性回歸的模型假設,這是最小二乘方法的優越性前提,否則不能推出最小二乘是最佳(即方差最小)的無偏估計
- 相比梯度下降,當n不是很大時,最小得到結果更快一些,一般線性回歸問題更偏向運用最小二乘法,但是梯度下降法在機器學習中適用範圍更大
梯度下降法:
- 得到的是局部最優解,因為是一步步迭代的,而非直接求得極值
- 既可以用於線性模型,也可以用於非線性模型,沒有特殊的限制和假設條件
- 梯度下降演算法有時需要我們對特征值進行適當的縮放,提高求解效率,需要進行數據歸一化處理
- 梯度下降演算法需要我們自己選擇適當的學習率α ,且需要多次的迭代運算
- 當n很大時,這時矩陣運算的代價就變的很大,最小二乘求解也會變的很慢,所以梯度下降更適合特征變數很多的情況,一般n小於10000時,選擇正規方程是沒問題的
線性回歸的正則化
為瞭解決過擬合問題,在損失函數中引入了正則化。我們常用的正則化一般是L1正則化和L2正則化。而線性回歸因為引入的正則化項不同,從而出現了Ridge回歸、Lasso回歸以及ElasticNet回歸。
L1正則化Lasso回歸:
線性回歸的L1正則化通常稱為Lasso回歸,它和一般線性回歸的區別是在損失函數上增加了一個L1正則化的項,L1正則化的項有一個常數繫數α來調節損失函數的均方差項和正則化項的權重,具體Lasso回歸的損失函數表達式如下:

其中n為樣本個數,α為常數繫數,需要進行調優。|θ|1為L1範數。Lasso回歸可以使得一些特征的繫數變小,甚至還是一些絕對值較小的繫數直接變為0。增強模型的泛化能力。關於求解,因為L1範數的原因,導致損失函數不再是連續可導的。所以之前的梯度下降法等演算法失效,需要另尋它法。Lasso回歸的求解辦法一般有坐標軸下降法(coordinate descent)和最小角回歸法( Least Angle Regression)。
L2正則化Ridge回歸:
L2正則化通常稱為Ridge回歸,它和一般線性回歸的區別是在損失函數上增加了一個L2正則化的項,和Lasso回歸的區別是Ridge回歸的正則化項是L2範數,而Lasso回歸的正則化項是L1範數。具體Ridge回歸的損失函數表達式如下:
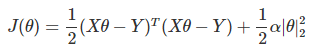
其中α為常數繫數,需要進行調優。|θ|2為L2範數。Ridge回歸在不拋棄任何一個特征的情況下,縮小了回歸繫數,使得模型相對而言比較的穩定,但和Lasso回歸比,這會使得模型的特征留的特別多,模型解釋性差。Ridge回歸的求解比較簡單,一般用最小二乘法。這裡給出用最小二乘法的矩陣推導形式,和普通線性回歸類似。
正則化之後的損失函數求解過程推薦參考博客:https://www.cnblogs.com/pinard/p/6018889.html
正則化求解之後的理解:
嶺回歸就是給模型參數加一個懲罰項,限制參數的大小。 通過引入該懲罰項,可以減少不重要的參數,這個技術在統計學中也叫做縮減(shrinkage)。(嶺回歸解決數據的輸入變數數目比樣本點還多的問題)。嶺回歸的本質是給參數增加了一個限制條件,即懲罰項,嶺回歸相當於增加瞭如下的約束:
上式限定了所有回歸繫數的平方和不能大於 。所以在嶺回歸中,有時稱為“L2回歸”,懲罰因數是變數繫數的平方值之和。懲罰因數縮小了自變數的繫數,但從來沒有完全消除它們。這意味著通過嶺回歸,您的模型中的雜訊將始終被您的模型考慮在內。與嶺回歸類似,另一個縮減方法lasso也對回歸繫數做了限定,對應的約束條件如下:
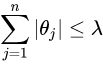
當 足夠小時,一些繫數會因此縮減到0,這個特性幫助我們更好的理解數據,但是這個變化卻導致計算複雜度大大提升,因為求解這個約束條件下的回歸繫數,需要使用二次規划算法。Lasso模型可以用來估計“稀疏參數”。在某些情況下Lasso非常有用,由於它的懲罰條件比較嚴格,所以傾向於選擇參數值較少的解,從而有效地減少了給定解所依賴的參數的數量。簡單說,如果你想要的最優解包含的參數數量越少越好,那麼使用Lasso是個很好的選擇。例如當你想從雜訊和信號的疊加中得到信號時。
在LASSO正則化中,只需懲罰高繫數特征,而不是懲罰數據中的每個特征。此外,LASSO能夠將繫數一直縮小到零。這基本上會從數據集中刪除這些特征,因為它們的“權重”現在為零(即它們實際上是乘以零)。通過LASSO回歸,模型有可能消除大部分雜訊在數據集中。這在某些情況下非常有用!
ElasticNet回歸:
ElasticNet回歸是對Lasso回歸和嶺回歸的一個綜合,它的懲罰項是L1範數和L2範數的一個權衡。損失函數為: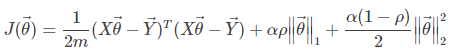
其中,α和ρ均為超參數,α≥0,1≥ρ≥0。而ρ影響的是性能下降的速度,因為這個參數控制著兩個正則化項之間的比例。
不同正則化之間的比較:
Lasso回歸(縮減繫數):可以使得一些特征繫數變小,甚至一些絕對值較小的繫數直接變為零,從而增強模型的泛化能力。因此很適合與參數數目縮減與參數的選擇,作為用來估計稀疏參數的線性模型。當進行模型選擇的時候,如果特征特別多,需要進行壓縮時,就可以選擇Lasso回歸。
Ridge回歸(平滑繫數):是在不拋棄任何一個特征的情況下,限制(縮小)了回歸繫數,使得模型相對而言比較複雜。和Lasso回歸相比,這會使得模型保留的特別多,導致解釋性差。
ElasticNet回歸:則是對上面兩個進行了權衡。實際上,L1L1正則項可以得到稀疏的θ⃗ θ→,L2L2正則項則可以得到比較小的θ⃗ θ→,ElasticNet回歸就是將這兩個結合著用。
線性回歸的推廣:多項式線性回歸
我們遇到的數據不一定都是線性的形式,如果是  的模型,那線性回歸很難擬合這個函數,這時候就需要用到多項式回歸了。回到我們開始的線性模型,
的模型,那線性回歸很難擬合這個函數,這時候就需要用到多項式回歸了。回到我們開始的線性模型,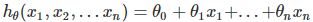 , 如果這裡不僅僅是x的一次方,而是二次方,那麼模型就變成了多項式回歸。這裡寫一個只有兩個特征的2次多項式回歸的模型:
, 如果這裡不僅僅是x的一次方,而是二次方,那麼模型就變成了多項式回歸。這裡寫一個只有兩個特征的2次多項式回歸的模型: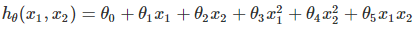 我們令
我們令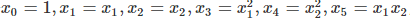 ,,這樣我們就得到了下式:
,,這樣我們就得到了下式: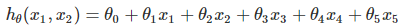 。可以發現,我們又重新回到了線性回歸,這是一個五元線性回歸,可以用線性回歸的方法來完成演算法。對於每個二元樣本特征
。可以發現,我們又重新回到了線性回歸,這是一個五元線性回歸,可以用線性回歸的方法來完成演算法。對於每個二元樣本特征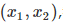 我們得到一個五元樣本特征
我們得到一個五元樣本特征  ,通過這個改進的五元樣本特征,我們重新把不是線性回歸的函數變回線性回歸,但是達到了非線性擬合的效果。
,通過這個改進的五元樣本特征,我們重新把不是線性回歸的函數變回線性回歸,但是達到了非線性擬合的效果。
線性回歸的推廣:廣義線性回歸
在上一節的線性回歸的多項式中,我們對樣本特征進行了變換,用線性回歸完成了非線性回歸的效果。這裡我們對於特征y做推廣。比如我們的輸出Y不滿足和X的線性關係,但是logY和X滿足線性關係,模型函數如下: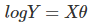 ,這樣對與每個樣本的輸入y,我們用logy去對應, 從而仍然可以用線性回歸的演算法去處理這個問題。我們把 logy一般化,假設這個函數是單調可微函數g(.),則一般化的廣義線性回歸形式是:
,這樣對與每個樣本的輸入y,我們用logy去對應, 從而仍然可以用線性回歸的演算法去處理這個問題。我們把 logy一般化,假設這個函數是單調可微函數g(.),則一般化的廣義線性回歸形式是: 。這個函數g(.)我們通常稱為聯繫函數。後面會講到的邏輯回歸這是在聯繫函數的基礎上進行分類的。
。這個函數g(.)我們通常稱為聯繫函數。後面會講到的邏輯回歸這是在聯繫函數的基礎上進行分類的。
總結:
最簡單的單變數線性回歸:
多變數線性回歸模型:
多項式回歸模型: 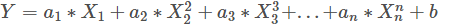
線性回歸的優點:
1. 建模速度快,不需要很複雜的計算,在數據量大的情況下依然運行速度很快;
2. 可以根據繫數給出每個變數的理解和解釋;
3. 對異常值很敏感。
線性回歸的缺點:
1. 不能很好的擬合非線性數據,所以需要先判斷變數之間是否線性相關。
多項式回歸的特點:
1. 能夠擬合非線性可分的數據,更加靈活的處理複雜的關係
2. 因為需要設置變數的指數,所以它是完全控制要素變數的建模
多項式回歸的特點:
1. 需要一些數據的先驗知識才能選擇最佳指數
2. 如果指數選擇不當容易出現過擬合
參考文章:
https://www.cnblogs.com/pinard/p/6004041.html
https://zhuanlan.zhihu.com/p/48205156
https://zhuanlan.zhihu.com/p/45023349
https://zhuanlan.zhihu.com/p/45690499
https://blog.csdn.net/fengxinlinux/article/details/86556584



