關係數據結構 列:對象某一方面的特征 行:一個對象各個方面的特征 關係模型的數據結構是單一的關係,關係模型的數據結構是一張扁平的二維表,實體以及實體間的聯繫均用二維表來表示,關係模型建立在集合代數的基礎上 外碼:設F是基本關係R的一個或一組屬性,它不是R的碼,KS是基本關係S的主碼,如果F與KS相對 ...
關係數據結構
列:對象某一方面的特征
行:一個對象各個方面的特征

關係模型的數據結構是單一的關係,關係模型的數據結構是一張扁平的二維表,實體以及實體間的聯繫均用二維表來表示,關係模型建立在集合代數的基礎上


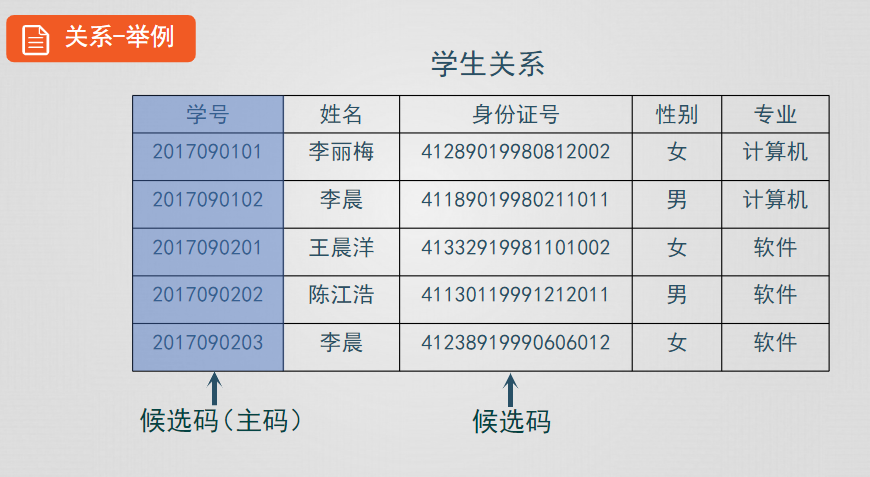
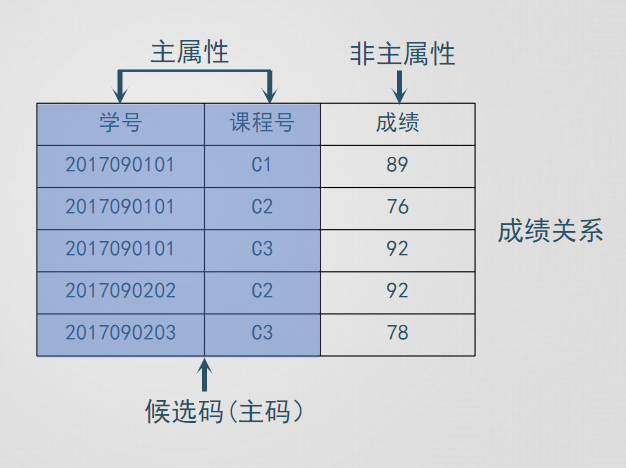
外碼:設F是基本關係R的一個或一組屬性,它不是R的碼,KS是基本關係S的主碼,如果F與KS相對應,則F稱為R的外碼。並稱關係R為參照關係,關係S為被參照關係
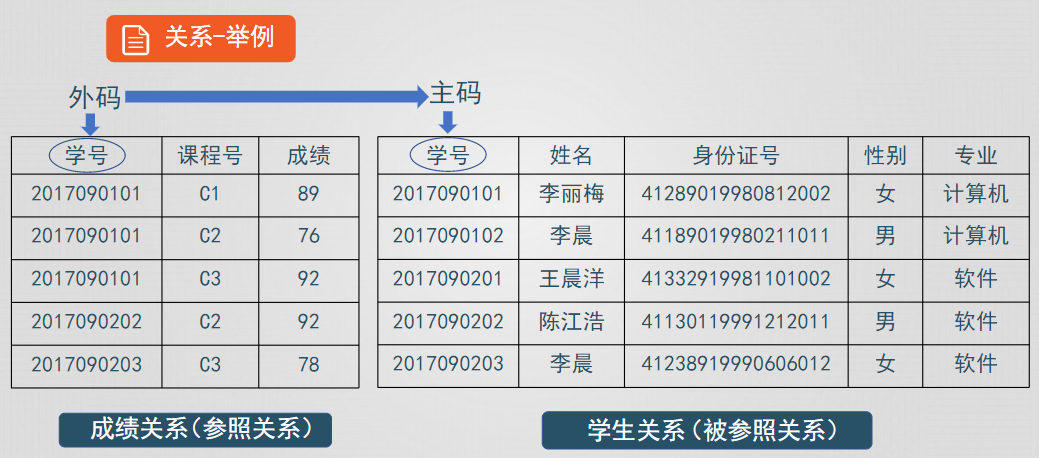
- 關係模型建立在集合代數基礎上
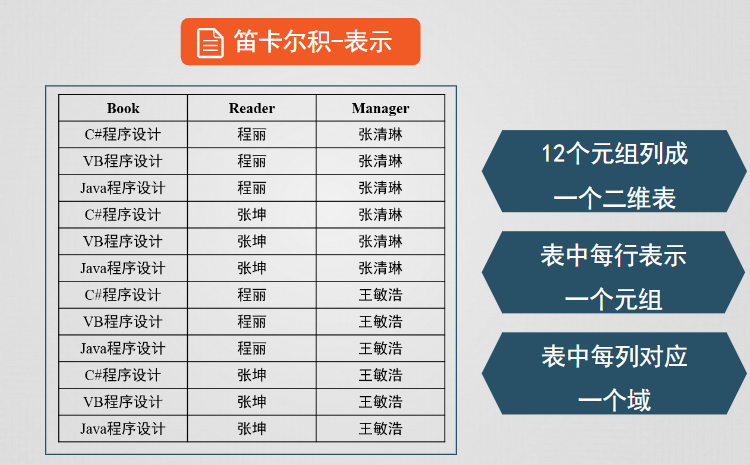
- 關係數據結構是二維表
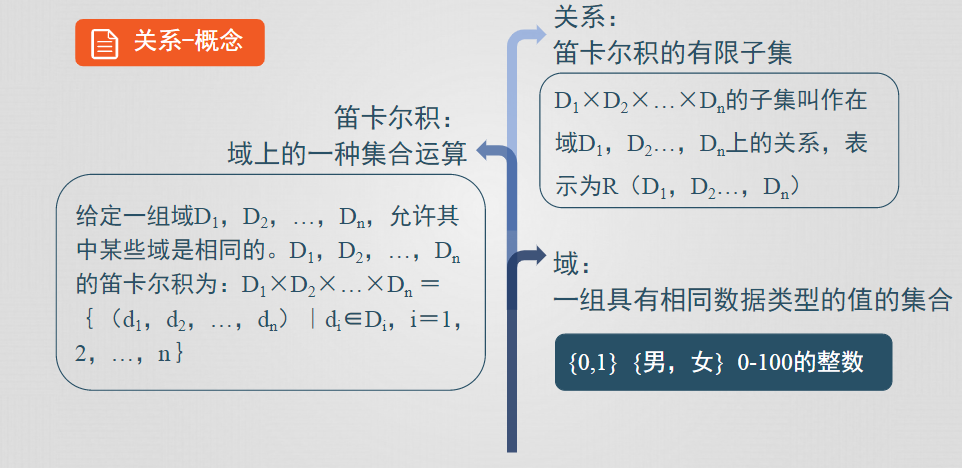
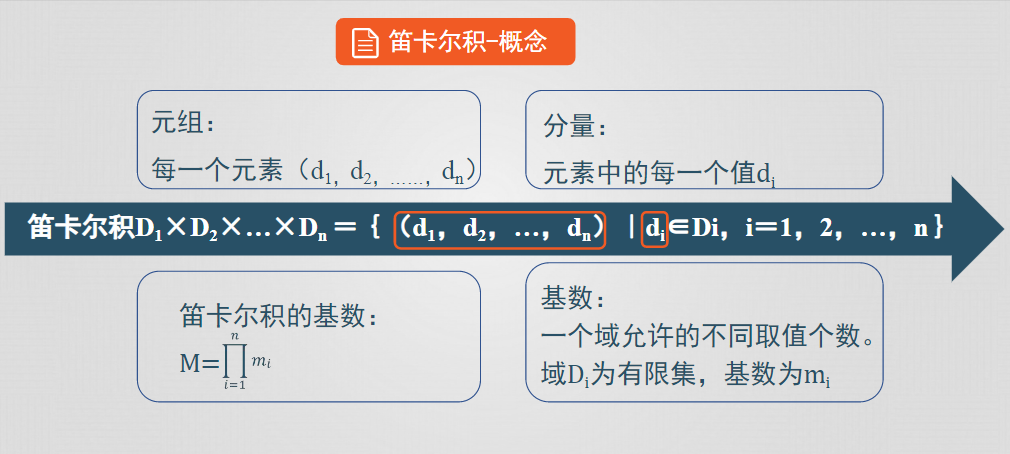
- 笛卡爾積是域上的集合運算
- 關係是笛卡爾積的有限子集
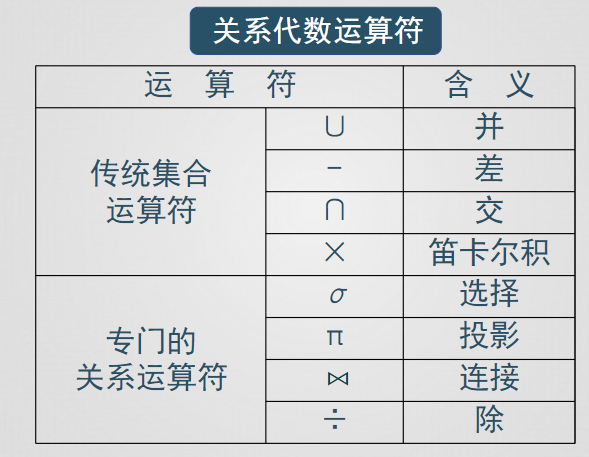
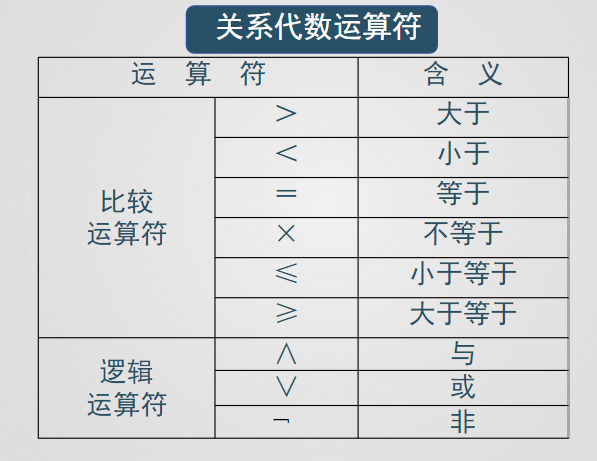
傳統集合運算
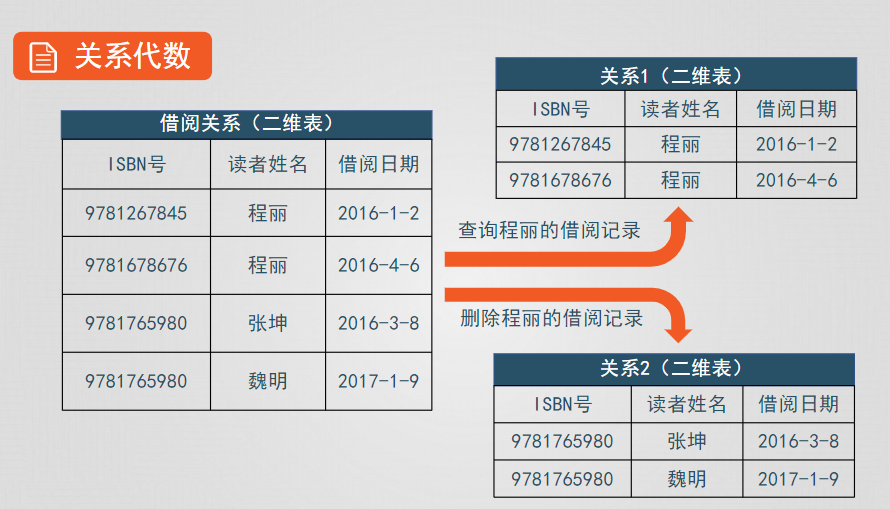
關係代數是一種抽象的查詢語言,它用對關係的運算來表達查詢
關係代數定義了一些操作,運用這些操作可以從一個或多個關係得到另一個關係,關係代數運算的對象是關係,運算的結果也是關係
並
設關係R和S具有相同的屬性個數n,且相應的屬性取自同一個域,t是R的一個元組(t∈R)。


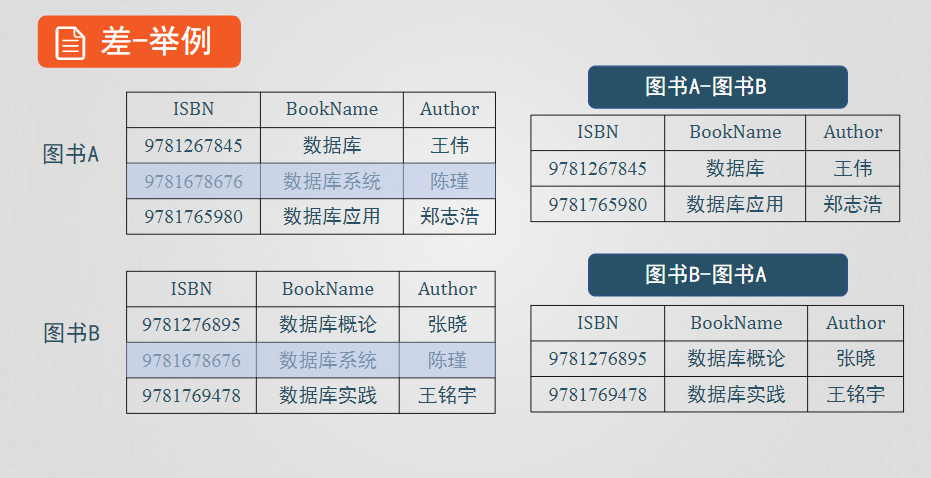
差
設關係R和S具有相同的屬性個數n,且相應的屬性取自同一個域,t是R的一個元組(t∈R)

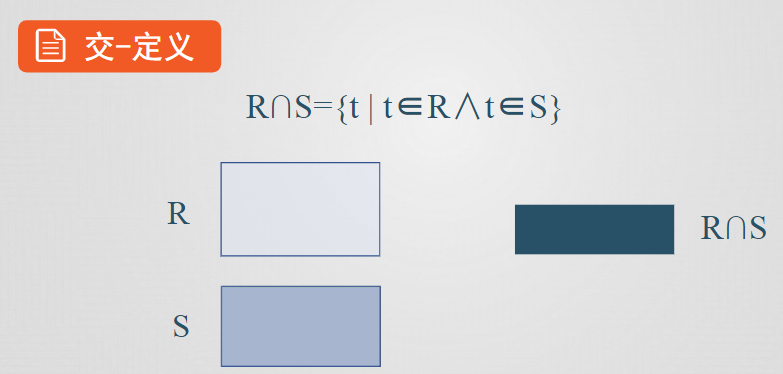
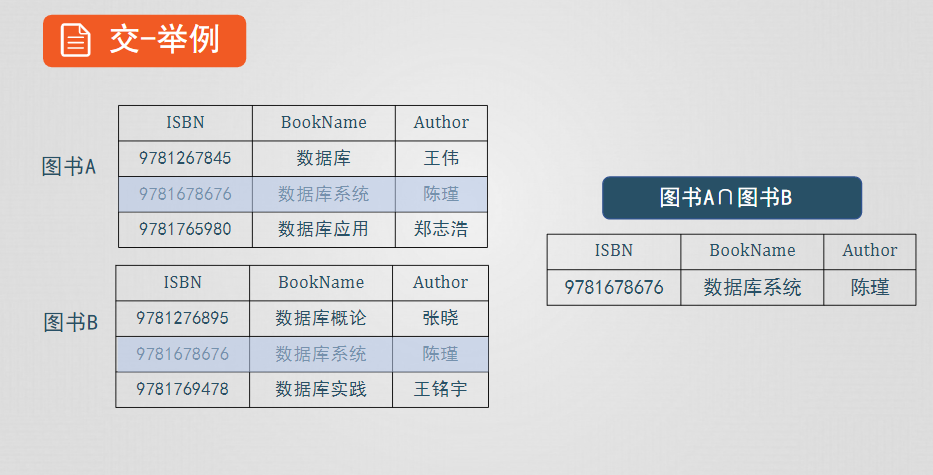
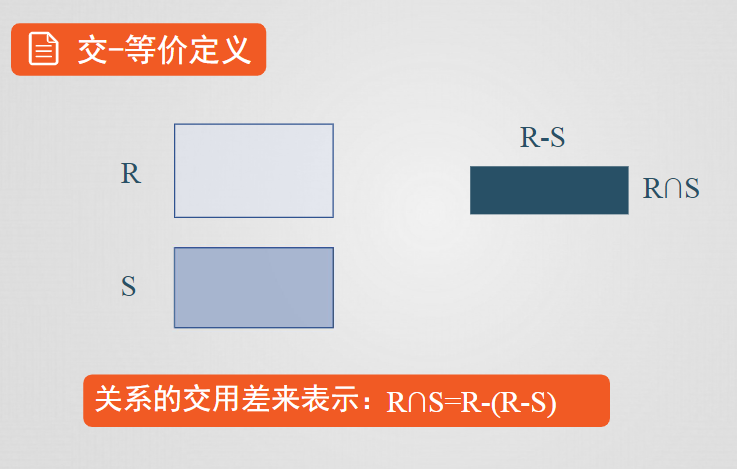
交
設關係R和S具有相同的屬性個數n,且相應的屬性取自同一個域,t是R的一個元組(t∈R)
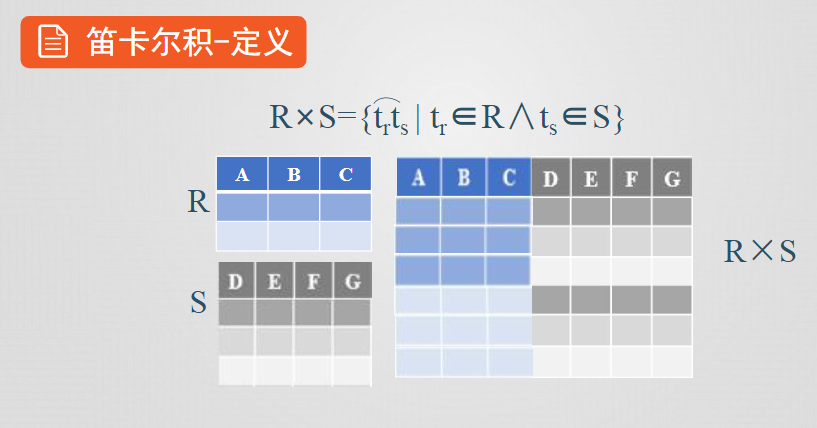
笛卡爾積
設關係R的屬性個數為n,關係S的屬性個數為m;R有k1個元組,S有k2個元組

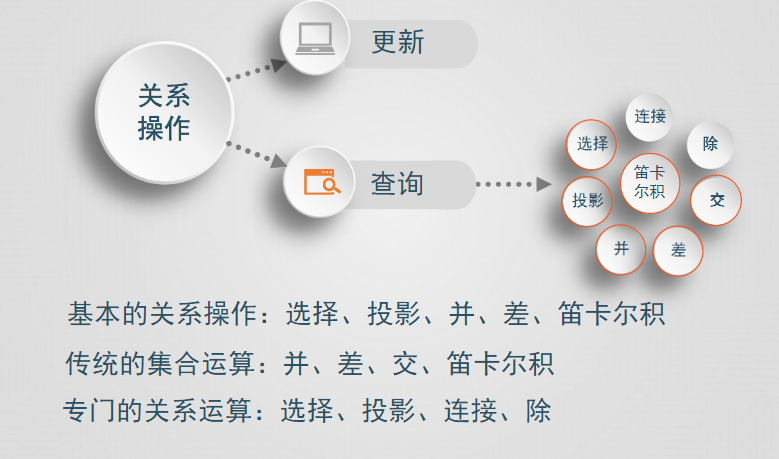
關係代數用對關係的運算表達查詢,主要分為傳統集合運算和專門的關係運算,傳統的集合運算包括並、交、差、笛卡爾積,統的集合運算是從行的角度進行的二目運算
選擇,投影

選擇運算是從指定的關係中選擇滿足給定條件的元組而組成一個新的關係


投影運算是從關係R中選擇若幹屬性列組成一個新的關係。


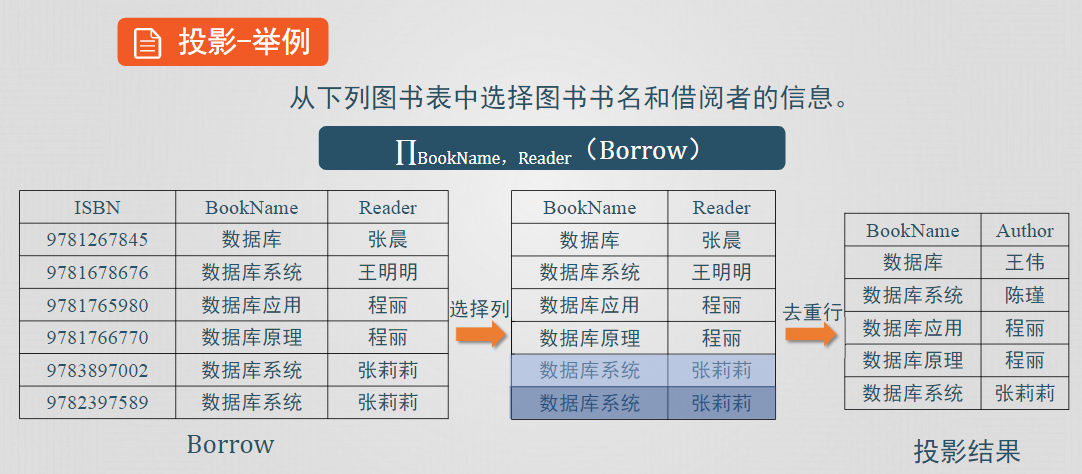
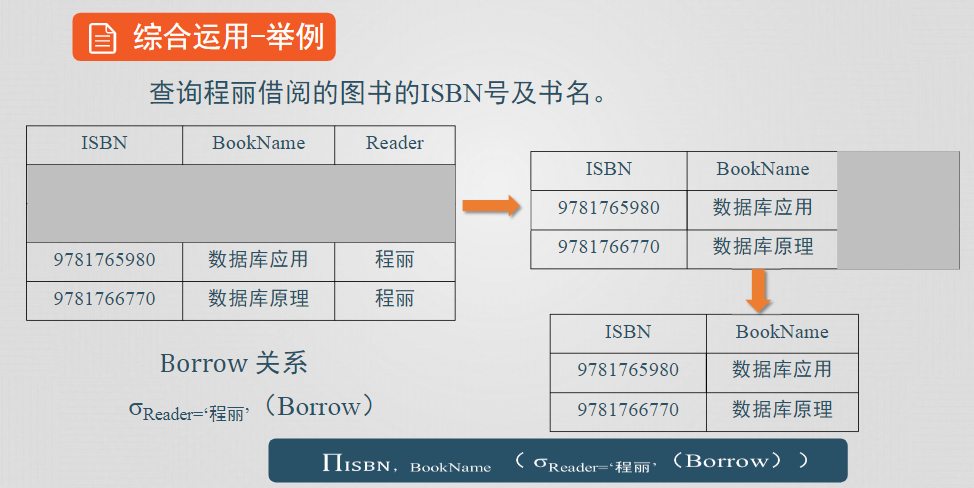
選擇運算從關係中選擇滿足條件的行,是從行的角度進行運算,投影操作從關係中選擇需要的列,是從列的角度進行運算
連接
連接運算是從兩個關係的笛卡爾積中選取屬性間滿足一定條件的元組
一般連接
假設有兩個關係R和S,A是R中的屬性組,B是S中的屬性組,這兩個屬性組列數相同,而且取值是可以比較的
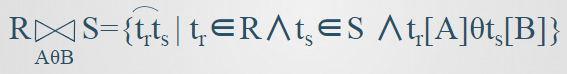

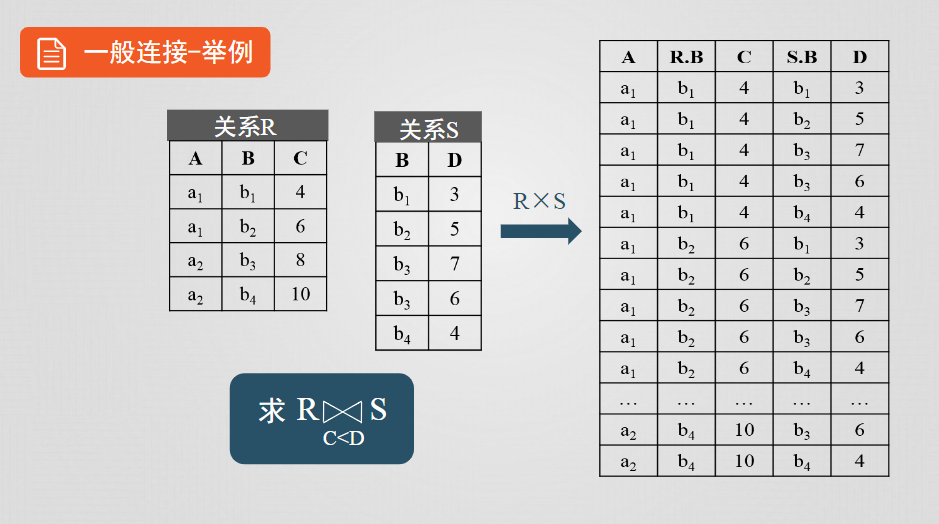
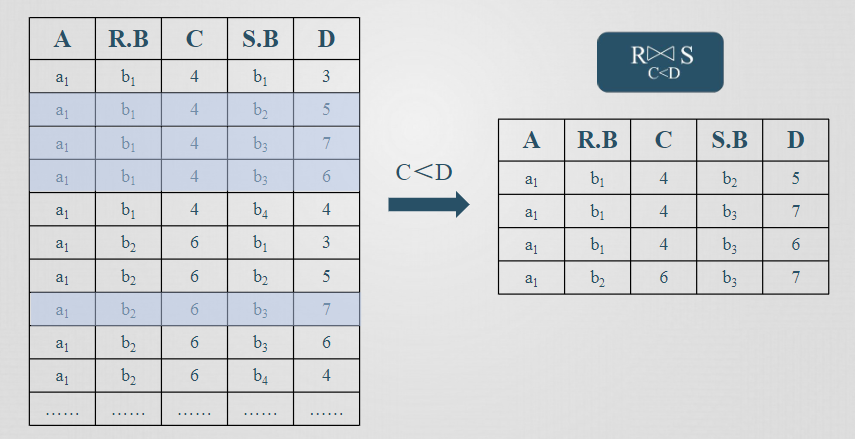
等值連接

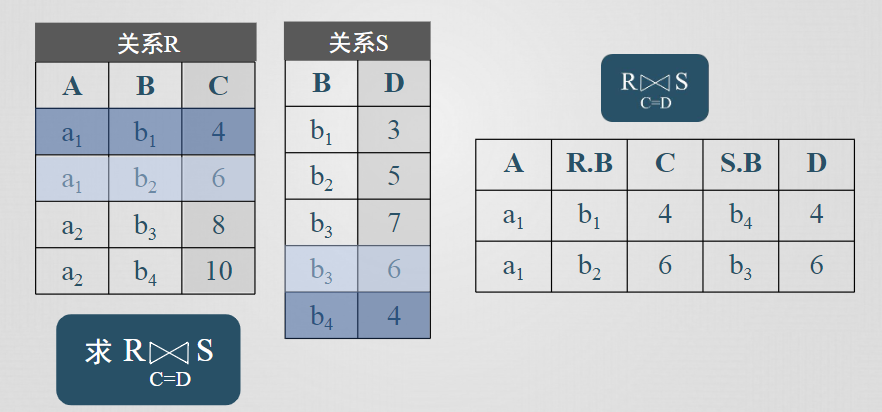
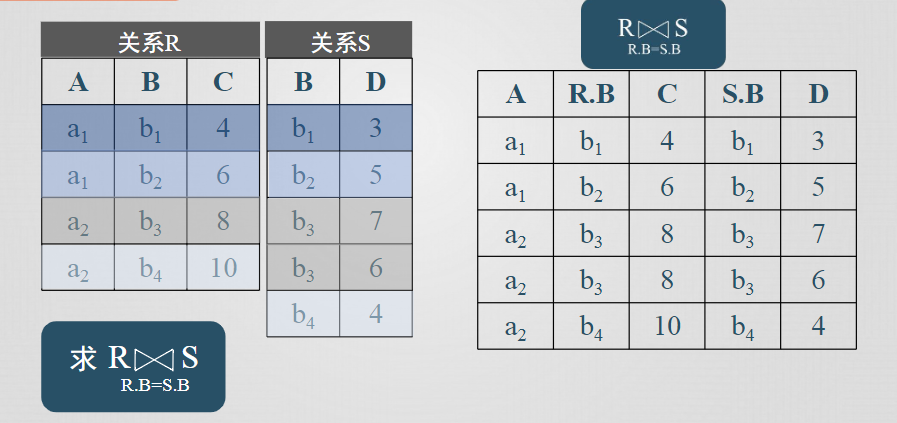
自然連接
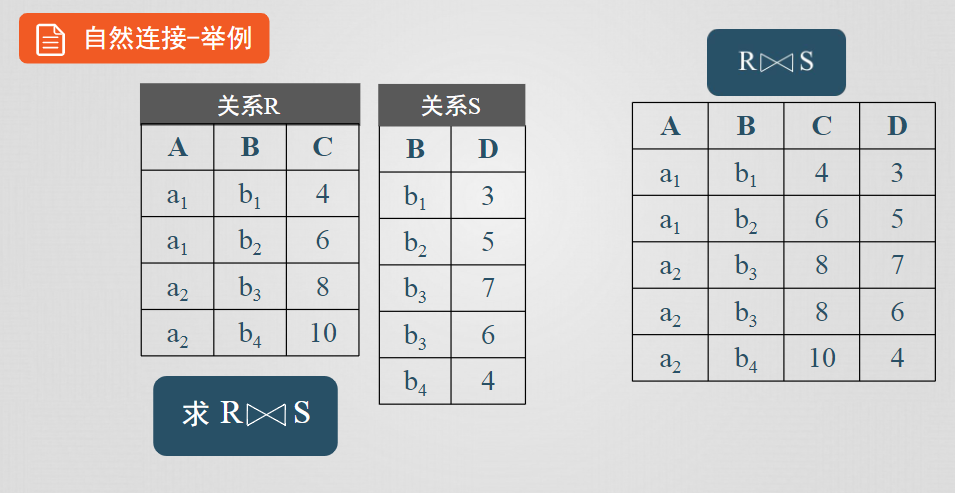

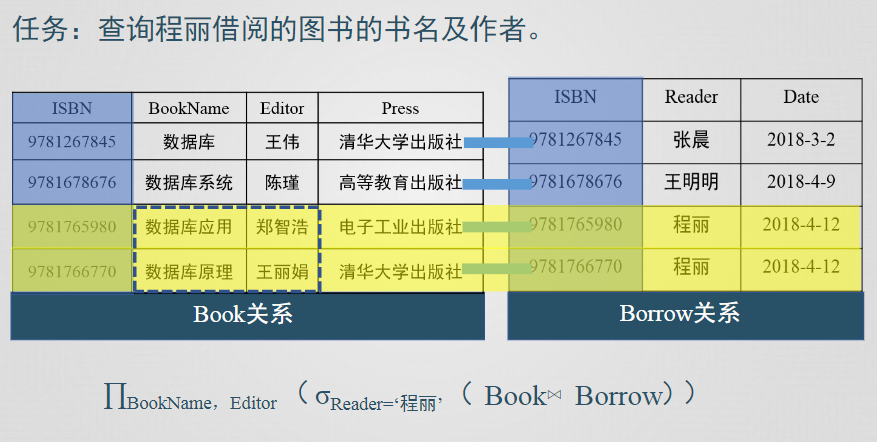
連接運算從兩個關係的笛卡兒積中選取屬性間滿足一定條件的元組,等值連接和自然連接是連接運算的兩種最為重要也最為常用的類型
除運算

給定關係R(X,Y)和S(Y,Z),其中X、Y、Z為屬性組。R中的Y與S中的Y可以有不同的屬性名,但必須出自相同的域。R與S的除運算得到一個新的關係P(X),P是R中滿足下列條件的元組在X屬性列上的投影元組在X上分量值x的象集Y x 包含S在 Y上投影的集合。記作:其中Y x 為x在R中的象集,x=t r [X]。定 義R÷S={t r [X]|t r ∈R∧∏ Y (S)⊆Yx }
除運算-步驟
(1)計算S在屬性組Y上的投影
(2)計算關係R在屬性組X上的投影
(3)計算(2)結果中各元素在關係R中的象集
(4)判斷各個象集與(1)中投影的包含關係,若某個象集包含S在屬性組Y上的投影,則該象集對應的X上的分量值即為除運算的結果元素
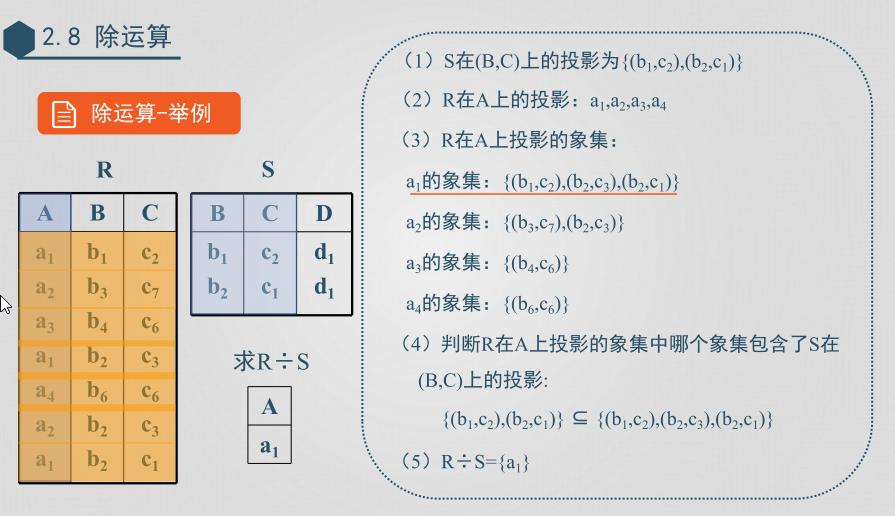
設有關係R(X,Y)和S(Y,Z),其中X、Y、Z為關係的屬性組。則:R (X,Y) ÷S(Y,Z)=R (X,Y) ÷∏ Y (S)
設關係S的屬性是R屬性的一部分,則R÷S為這樣的關係:
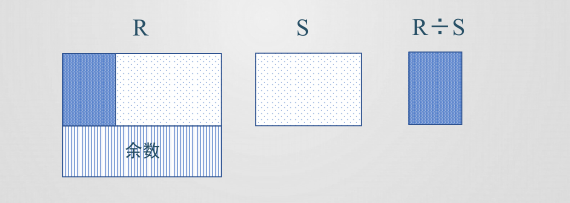
此關係的屬性由屬於R但不屬於S的所有屬性組成,此關係的任一元組都是R中某元組的一部分。且任取一個元組t,則t與S的任一元組連接後,都為R中原有的一個元組。
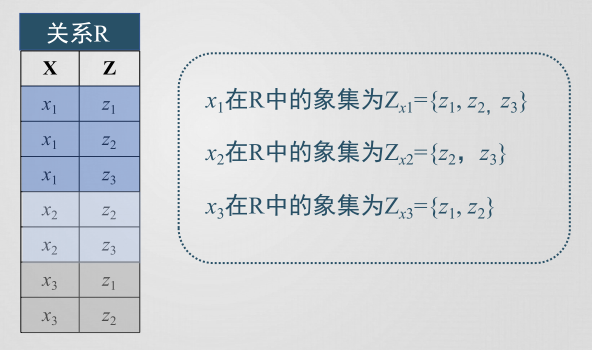
象集:x在R中的象集為R中屬性組X上值為x的諸元組在Z上分量的集合
根據除運算中判斷兩個集合是否存在包含關係這個特點,來決定問題的解決是否需要使用除運算。



