樹結構基礎 LCA c++ ……(省略,同LCA) int L[N], R[N];//每個子樹代表的區間 int tot;//總時間 //搜索整棵樹, 得到每個節點的深度 void dfs(int u, int f){//u: 一節點 f: 其節點的父親節點 L[u] = ++tot; dep[u] ...
樹結構基礎
LCA
在一棵樹中,有a,b二點,求它們的最近公共祖先dp[i][j]: i往上走2^j步
//初始化
dp[i][0] = fa[i] -> i的祖先(i往上走1(2^0)步)#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
const int M = 200010;
int head[N], pnt[M], nxt[M], E;
//head[a]: a這個頂點的邊; pnt[j]: j這條邊的底點; nxt[i]: i這條邊的上一條邊; E: 第E條邊
int dep[N], dp[N][20];
//初始化
void init(){
E = 0;
memset(head, -1, sizeof(head));
}
//加邊
void add(int a, int b){
pnt[E] = b;
nxt[E] = head[a];
head[a] = E++;//更新, 以a為頂點的邊(E++)
}
//搜索整棵樹, 得到每個節點的深度
void dfs(int u, int f){//u: 一節點 f: 其節點的父親節點
dep[u] = dep[f] + 1;//深度 父親節點+1
dp[u][0] = f;//u節點往上1個深度就是其父親節點
for(int i = head[u]; i != -1; i = nxt[i]){
int v = pnt[i];//u節點為父親節點, v為孩子節點
if(v != f){
dfs(v, u);//往下搜整棵樹
}
}
}
//log(n)時間查詢LCA
int ask(int x, int y){
if(dep[x] < dep[y]){//始終保證x在y下麵
swap(x, y);
}
int delta = dep[x] - dep[y];//深度差
//先跳到同一高度,x為較深的節點
for(int i = 0; i < 20; i++){//找最小的i, 使2^i <= delta
if(delta & (1 << i)){
x = dp[x][i];
}
}
if(x == y) return x;//二個節點相同, x是y的LCA, 直接返回
for(int i = 19; i >= 0; i--){//從大到小,先跨最大大
if(dp[x][i] != dp[y][i]){
x = dp[x][i];
y = dp[y][i];
}
}
return dp[x][0];//父親節點還需往上1個深度
}
int main(){
//建樹
dfs(1, 0);
for(int i = 1; i < 20; i++){
for(int j = 1; j <= n; j++){
dp[j][i] = dp[dp[j][i-1]][i-1];//2^i = 2^(i-1) + 2^(i-1)
}
}
//查詢
return 0;
}DFS序
DFS序就是將樹形結構轉化為線性結構,用dfs遍歷一遍這棵樹,進入到x節點有一個in時間戳,遞歸退出時有一個out
時間戳,x節點的兩個時間戳之間遍歷到的點,就是根為x的子樹的所有節點,他們的dfs進入時間戳是遞增的。同時兩個時間戳構成了一個區間,x節點在這段區間的最左端,這個區間就是一棵根節點為x的子樹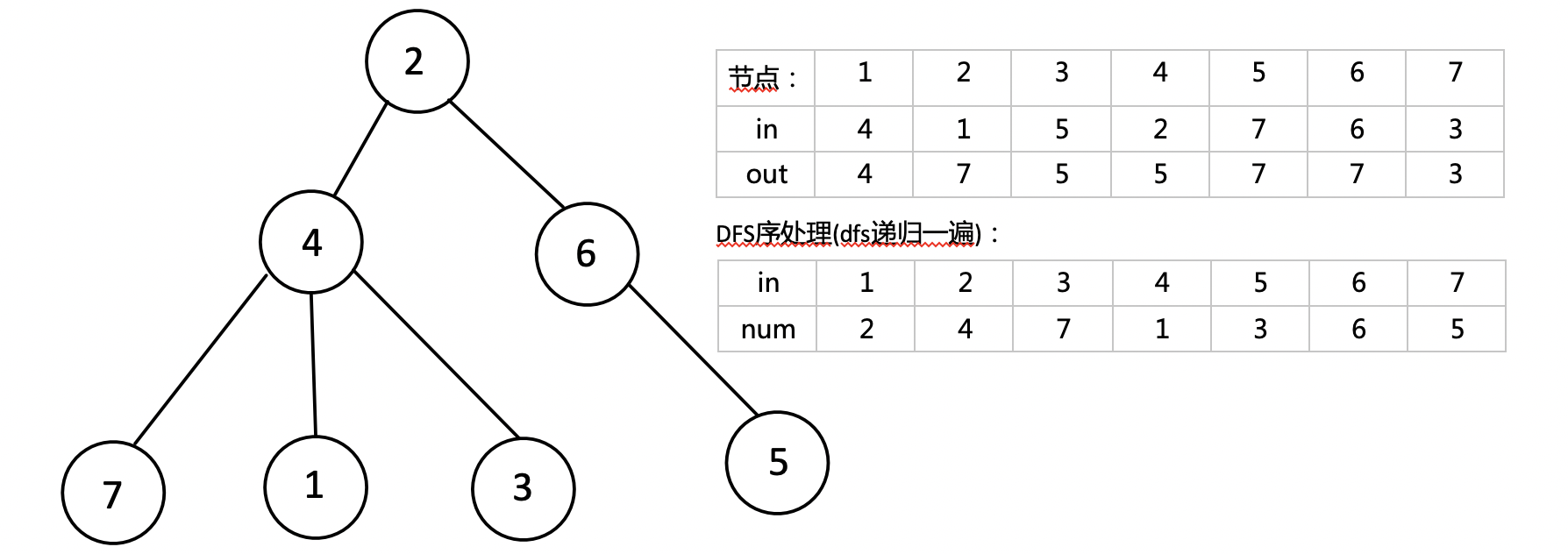
……(省略,同LCA)
int L[N], R[N];//每個子樹代表的區間
int tot;//總時間
//搜索整棵樹, 得到每個節點的深度
void dfs(int u, int f){//u: 一節點 f: 其節點的父親節點
L[u] = ++tot;
dep[u] = dep[f] + 1;//深度 父親節點+1
dp[u][0] = f;//u節點往上1個深度就是其父親節點
for(int i = head[u]; i != -1; i = nxt[i]){
int v = pnt[i];//u節點為父親節點, v為孩子節點
if(v != f){
dfs(v, u);//往下搜整棵樹
}
}
R[u] = tot;
}
……(省略,同LCA)歐拉序列
對一棵樹T進行遍歷,無論是遞歸還是回溯,每次到達一個節點就把編號記錄下來,得到一個長度為 2N−1 的序列,成為樹 T 的歐拉序列F
序列一:1 2 5 5 6 6 2 3 3 4 4 1
1. 入加出減,首碼和即為到根的權制和
2. 最後一次出現的位置的首碼和減去第一次出現的位置的首碼和即為子樹的首碼和……(省略,同LCA)
int s[N * 2], top;
//搜索整棵樹, 得到每個節點的深度
void dfs(int u, int f){//u: 一節點 f: 其節點的父親節點
s[++top] = u;
dep[u] = dep[f] + 1;//深度 父親節點+1
dp[u][0] = f;//u節點往上1個深度就是其父親節點
for(int i = head[u]; i != -1; i = nxt[i]){
int v = pnt[i];//u節點為父親節點, v為孩子節點
if(v != f){
dfs(v, u);//往下搜整棵樹
}
}
s[++top] = -u;
}
……(省略,同LCA)序列二: 1 2 5 5 2 6 6 2 1 3 3 1 4 4 1
兩個點第一次出現的位置之間的區間中深度最小的點就是LCA……(省略,同LCA)
int s[N * 2], top;
//搜索整棵樹, 得到每個節點的深度
void dfs(int u, int f){//u: 一節點 f: 其節點的父親節點
s[++top] = u;
dep[u] = dep[f] + 1;//深度 父親節點+1
dp[u][0] = f;//u節點往上1個深度就是其父親節點
for(int i = head[u]; i != -1; i = nxt[i]){
int v = pnt[i];//u節點為父親節點, v為孩子節點
if(v != f){
dfs(v, u);//往下搜整棵樹
s[++top] = u;//每次加完兒子,都要加一次自己
}
}
s[++top] = -u;
}
……(省略,同LCA)樹的重心
找到一個點,其所有的子樹中最大的子樹節點數最少,那麼這個點就是這棵樹的重心性質一:樹中所有點到某個點到距離之和中,到重心的距離之和是最小的,如果重心有多個則相同
性質二:把兩棵樹通過一條邊相連,新的樹的重心在他們的重心的連線上
性質三:把一棵樹添加或者刪除一個葉子,它的重心最多只移動一條邊的距離
性質四:一棵樹最多有兩個重心,且相鄰樹的直徑
一棵樹中最遠的兩個點,其路徑就是樹的直徑性質一:從樹中任意一點出發能走到的最遠的點一定是S-T中的一點,再從這個點出發就能搜到直徑
性質二:所有點直徑必定相交於連續的一段樹上差分
差分
一個數組中,一個位置與前一個位置的差數組a[N], 在L-R中加上V。
利用差分,a[L] = V(a[L]-a[L-1] = V), a[R+1] = -V(a[R+1]-a[R] = -V)
再用首碼和, a[L] - a[R]都視為加上了V樹上差分
每次給一條路徑加上值,問最後每條邊的權值


