查找的一些基本概念 查找表 是由同一類型的 數據元素 構成的集合,它是一種以查找為“核心”,同時包括其他運算的非常靈活的數據結構。 上面概念中的集合和數學上的定義是一致的,簡單地說就是由任意一些可分辨的對象構成的整體 作為一個數學概念,集合的元素是沒有任何限制。 作為一種數據結構,查找表的邏輯結構是 ...
查找的一些基本概念
查找表 是由同一類型的數據元素 構成的集合,它是一種以查找為“核心”,同時包括其他運算的非常靈活的數據結構。
上面概念中的集合和數學上的定義是一致的,簡單地說就是由任意一些可分辨的對象構成的整體
作為一個數學概念,集合的元素是沒有任何限制。
作為一種數據結構,查找表的邏輯結構是集合,對查找表進行的操作包括 查找表中的某一元素,讀取表中特定數據元素,插入和刪除一個數據元素等。
若對查找表只進行前兩項操作,則稱此類查找表為 靜態查找表。
若在查找過程中,向表中插入不存在的數據元素,或者從表中刪除某個數據元素,則稱此類查找表為動態查找表。
靜態查找表
順序表上的查找
具體的代碼就不實現了,有興趣的可以自行查閱,主要說的是概念與邏輯
對於查找運算,其基本操作是“數據元素的鍵值與給定值的比較”,所以通常用“數據元素的鍵值與給定值的比較次數”作為衡量查找演算法好壞的依據,稱上述比較次數為
查找長度。但是查找長度與鍵值在順序表中的位置有關,且差別很大。例如,若鍵值在順序表的第n個位置上,則查找長度為1,而如果鍵值在順序表的第1個位置上,查找長度為n。
基於上述內容引入一個新的概念,叫做“查找成功時的平均查找長度(記作ASL)”
它的定義是這樣的:為找到數據元素在查找表中的位置,與給定值進行比較的鍵值個數的期望值。
當查找表有n個元素時,有
$$ASL=\sum_{r=1}^nP_iC_i$$
其中P~i~為查找第i個元素(即給定值key與順序表中第i個元素的鍵值相等)的概率,且$\sum_{r=1}^nP_i=1$,C~i~表示在找第i個元素時,與給定值已進行比較的鍵值個數。
假設順序表為(b~1~,b~2~,b~3~)查找b~1~,b~2~,b~3~的概率分別是0.2,0.2,0.6,則順序查找法的平均查找長度為 $0.2 * 3+0.22+0.61 = 1.6$ 即平均需要1.6 次鍵值與給定值的比較才能找到待查元素。
由於多種元素P~i~值不好確定,所以通常讓P~i~概率相等,即對所有的i,有 $P_i =\frac{1}{n}$,併在此假設下確定查找演算法的平均查找長度。
$$ASL=\sum_{r=1}^nP_iC_i=\sum_{r=1}^n\frac{1}{n}*(n-i+1)=\frac{n+1}{2}$$
上述內容記住結論即可。
有序表上的查找
如果順序表中數據元素是按照鍵值大小的順序排列的,則稱為有序表。
這種存儲結構,查找運算可以用效率更高的二分查找法
直接看例題即可
現在有一個含有9個數據元素的有序表(關鍵字即為數據元素的值)
(10,13,17,20,30,55,68,89,95)用二分查找演算法查找key=17的過程
第一步,找到查找區間,合計9個數據元素,那麼[1,9]就是區間
(1+9)/ 2 = 5
找到位置5的數據元素30,30>17 進入第二步
第二步,縮小查找區間,合計4個數據元素,那麼[1,4]就是區間
(1+4)/ 2 = 2.5 去尾法 等於2
找到位置2的數據元素13,13<17 進入第三步
第三步,縮小查找區間,那麼[3,4]就是區間
(3+4) / 2 = 3.5 去尾法 等於3
找到位置3的數據元素17,正好是待查元素,查找成功,返回結果為mid=3
索引順序表上的查找
索引順序表由兩部分組成:一個索引表和一個順序表
其中 順序表在組織形式上與普通的順序表完全相同,而索引表本身在組織形式上也是一個順序表。
索引表通過索引將順序表分割為若幹塊,而順序表呈現出“按塊有序”的形式
若靜態查找表用索引順序表表示,則查找操作可用分塊查找來實現,也稱為 索引順序查找。
分為兩步進行:
(1)先確定待查數據元素所在的塊
(2)然後在塊內順序查找
結論:
靜態查找表 有順序查找、二分查找、分塊查找
三種特點分別為:
- 順序查找效率最低但限制最少
- 二分查找效率最高,但限制最多
- 分塊查找介於上述二者之間
二叉排序樹
一棵二叉排序樹(又稱二叉查找樹)具備如下性質
- 若它的左子樹不空,則左子樹上所有結點的鍵值均小於它的根結點鍵值;
- 若它的右子樹不空,則右子樹上所有結點的鍵值均小於它的根結點鍵值;
- 根的左、右子樹也分別為二叉排序樹。
二叉排序樹的案例如下圖所示
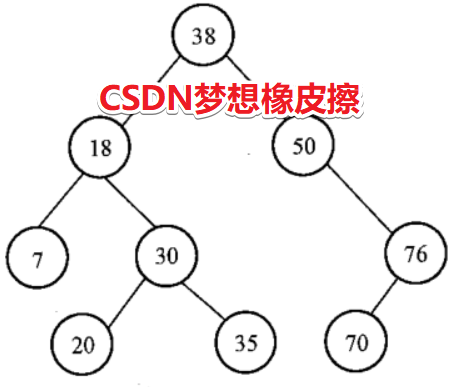
關於二叉排序樹,教材中涉及了部分代碼,分別如下
- 二叉排序樹上的查找
- 二叉排序樹上的插入
二叉排序樹的查找分析
需要記住的一些小點如下
二叉排序樹上的平均查找長度是介於O(n)和O($\log_2n$)之間。
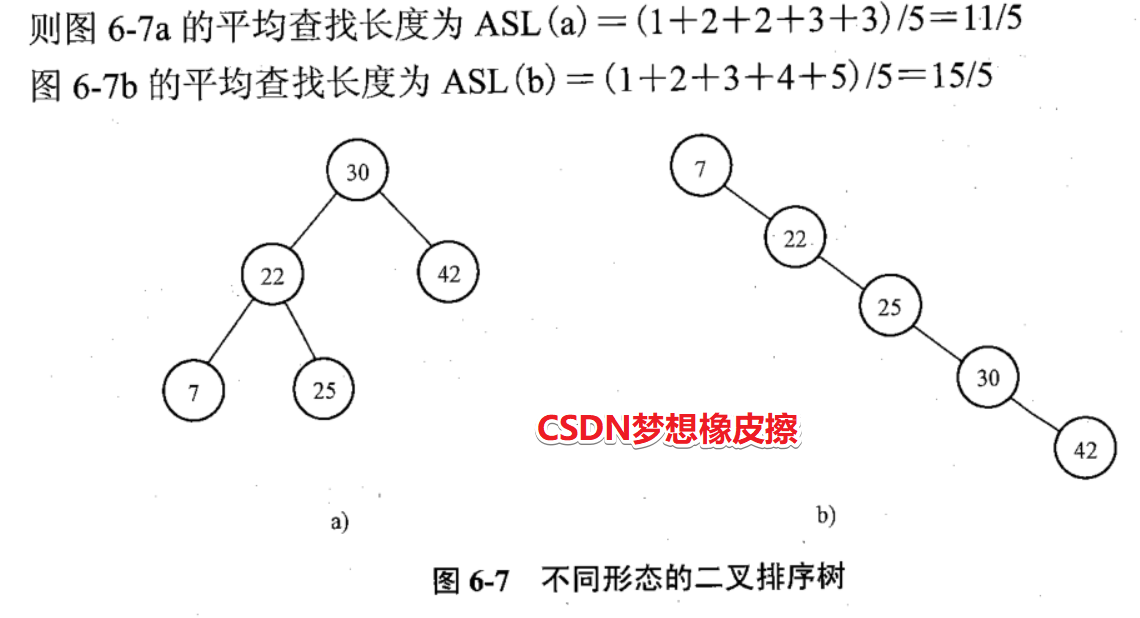
以下兩個樹的平均查找長度分別為
散列表
一些基本概念要普及一下
數據元素的鍵值和存儲位置之間建立的對應關係H成為散列函數,
用鍵值通過散列函數獲取存儲位置的這種存儲方式構造的存儲結構成為散列表,這一映射過程稱為散列
如果選定了某個散列函數H及其對應的散列表L,則對每個數據元素X,函數值H(H.Key)就是X在散列表L中的存儲位置,這個存儲位置也稱為散列地址。
常用的散列法
構造散列函數的方法,瞭解一下
- 數字分析法
- 除留餘數法
- 平方取中法
- 基數轉換法
散列表的實現(自考必考,不是考代碼,是考方法)
線性探測法
直接用例題與動畫來解釋吧
題目要求
設散列表長度為11,散列函數H(key) = key mod 11(mod為求餘運算),給定的健值序列為(3,12,13,27,34,22,38,25),試畫出採用線性探測法解決衝突時所構造的散列表,並求出在等概率的情況下查找成功時的平均查找長度。
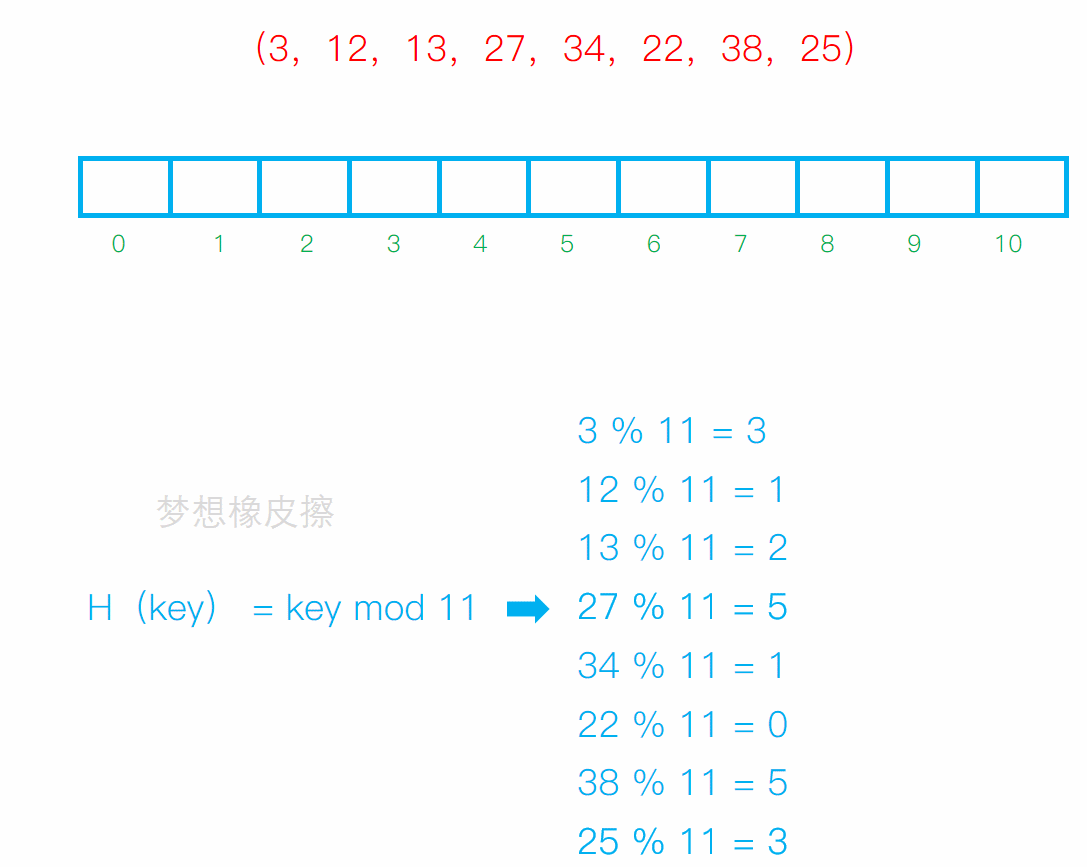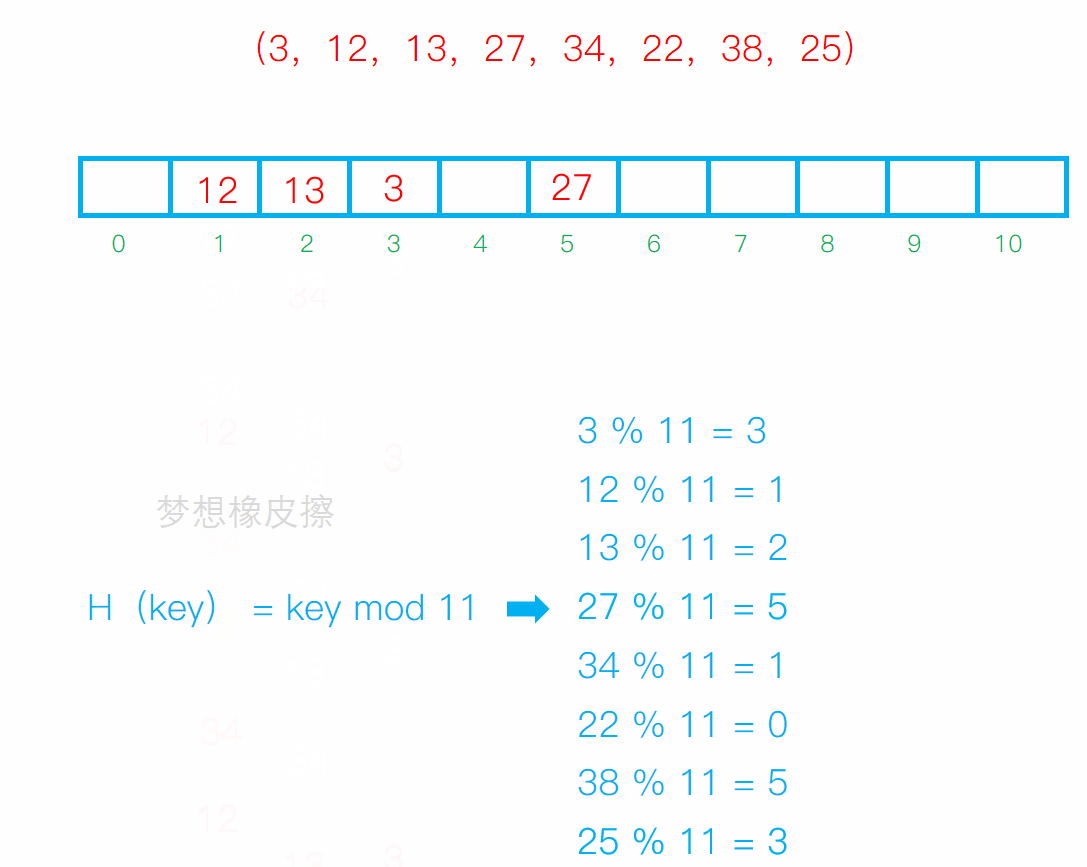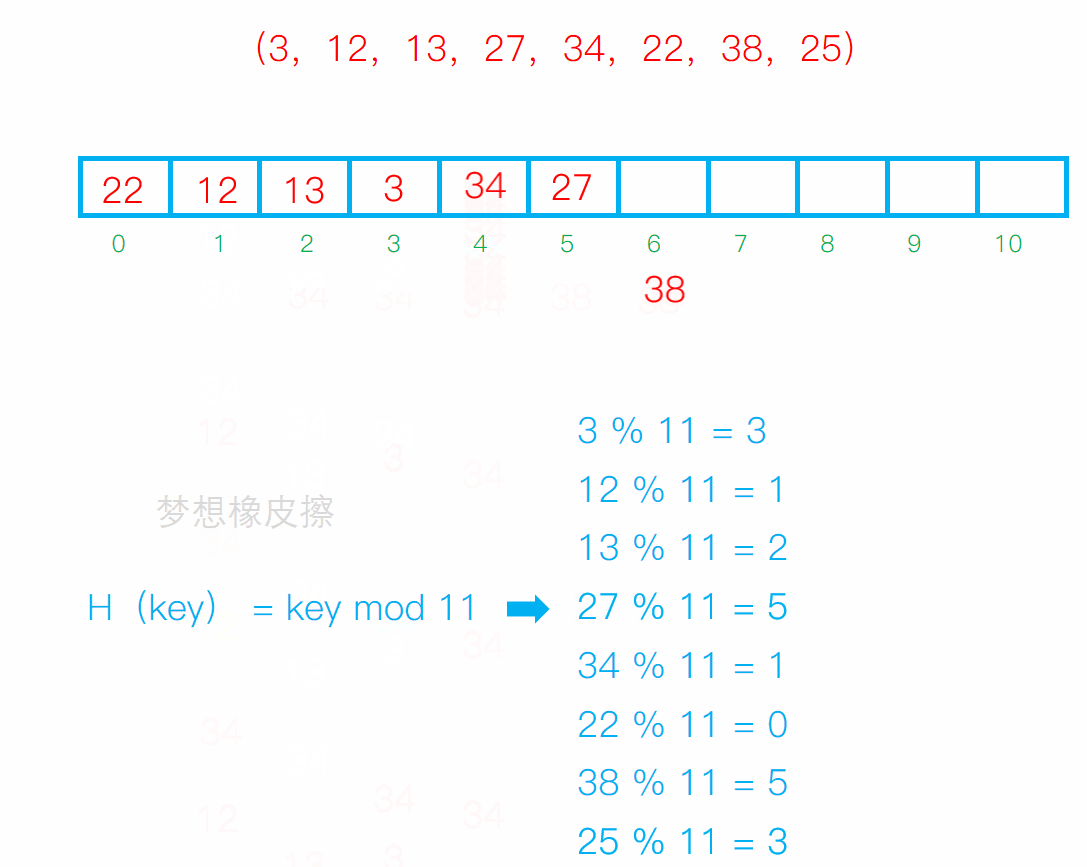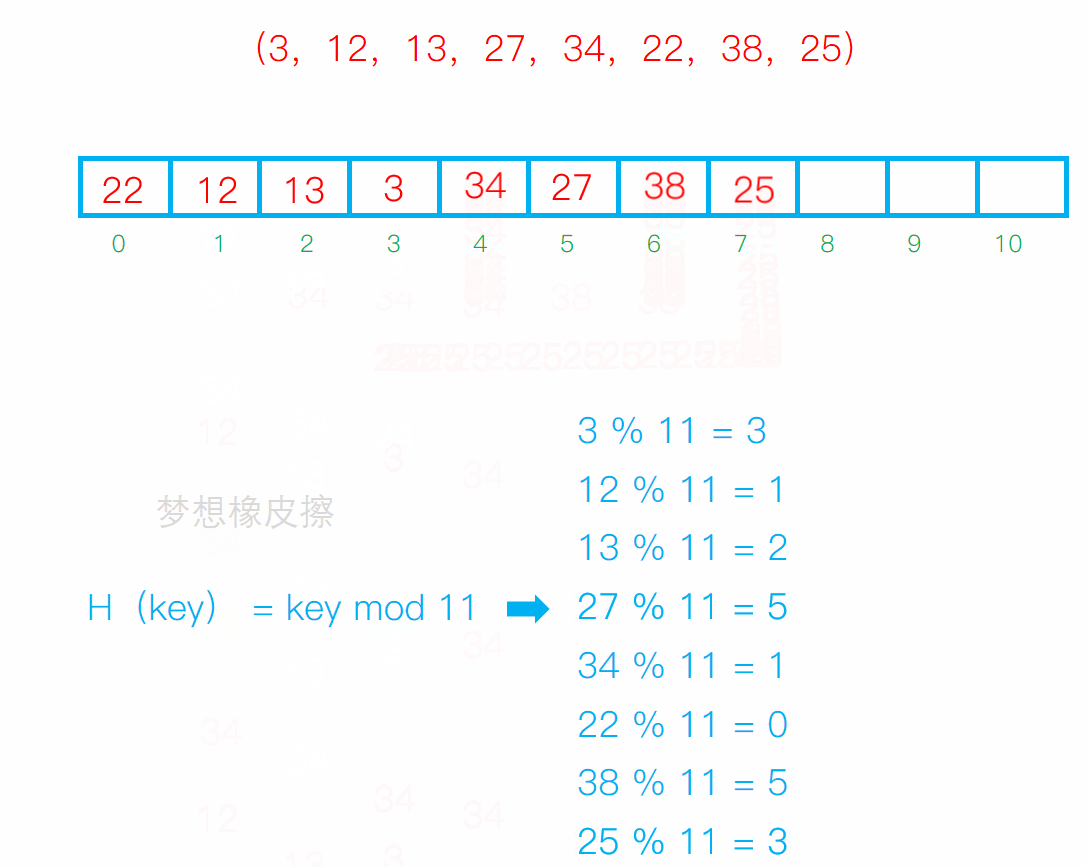
線性探測法 就是 求餘數,然後放到對應的位置上,如果位置上有數據元素了,那麼就向後移動,移動到沒有數據元素的位置上,然後占坑
平均查找長度 ASL 就是把元素查找次數加起來總和/散列表長度 = 16/11
二次探測法
二次探測法,核心在於二次上,說白了,就是當你取餘得到的位置由數據元素的時候,需要進行二次的偏移探測
例如,還是上述的題目,當計算到34的時候,發現位置1已經有元素了,接下來就要進行二次探測了
用1的位置分別進行+1^2^,-1^2^,+2^2^,-2^2^...
第一步,探測1+1^2^ = 2 ,位置2是否存在元素,發現有
第二步,探測1-1^2^ = 0,位置0是否存在元素,發現無,那麼好,把34放在位置0那裡,假設位置0也有元素了
第三步,探測1+2^2^ = 5,位置5是否存在元素,發現無,把34放過去。
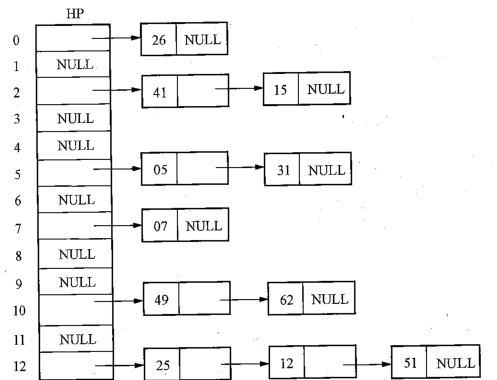
鏈地址探測法
可以通過一個案例來簡單說明一下
選定一個散列函數H(key) = key mod 13 ,鍵值為26,41,25,05,07,15,12,49,51,31,62
然後我們把求到的餘數,依次對應到鄰接表裡面,如下圖(直接截取教材圖了,就不畫了)
公共溢出區法(選看)
更多圖示: https://dwz.cn/r4lCXEuL
小結
本章在自考或者期末考試中,核心內容是二分查找方法;二叉排序樹的構建,散列表的查找方法,重點會考察線性探測法和二次探測法,重點看一下吧。
BYEBYE~



