判定樹和哈夫曼樹 分類與判定樹 這個小節有個比較重要的概念,就是 記住即可 哈夫曼樹與哈夫曼演算法 首先瞭解一下什麼是哈夫曼樹 給定一組值p~1~,...p~k~,如何構造一棵有k個葉子且分別以這些值為權的判定樹,使得其平均比較次數最小。滿足上述條件的判定樹稱為哈夫曼樹。 哈夫曼率先給出了一個求哈夫曼 ...
判定樹和哈夫曼樹
分類與判定樹
這個小節有個比較重要的概念,就是用於描述分類過程的二叉樹稱為判定樹 記住即可
哈夫曼樹與哈夫曼演算法
首先瞭解一下什麼是哈夫曼樹
給定一組值p~1~,...p~k~,如何構造一棵有k個葉子且分別以這些值為權的判定樹,使得其平均比較次數最小。滿足上述條件的判定樹稱為哈夫曼樹。
哈夫曼率先給出了一個求哈夫曼樹的簡單而有效的方法,稱為哈夫曼演算法。
非形式的描述如下
- 給定的值{p~1~,p~2~,...,p~k~}構造森林{T~1~,T~2~,T~k~},其中每個T~i~為一棵只有根結點且其權為p~i~的二叉樹。
- 從F中選取根結點的權最小的兩棵二叉樹T~i~和T~j~,構造一棵分別以T~i~和T~j~為左、右子樹的新的二叉樹T~h~,置T~h~根結點的權為T~i~,T~j~根結點的權值之和。
- 從F中刪去T~i~和T~j~,並將T~h~加入F,若F中仍多於一棵二叉樹,則返回第二步,直到F中只含有一棵二叉樹為止,這棵樹就是哈夫曼樹。
參照案例

重點來了,看真題,請記住==哈夫曼樹不唯一、時刻考慮權值最小==
真題參考

動態展示這道題目的解答方法,已經去掉了結點之間的連線
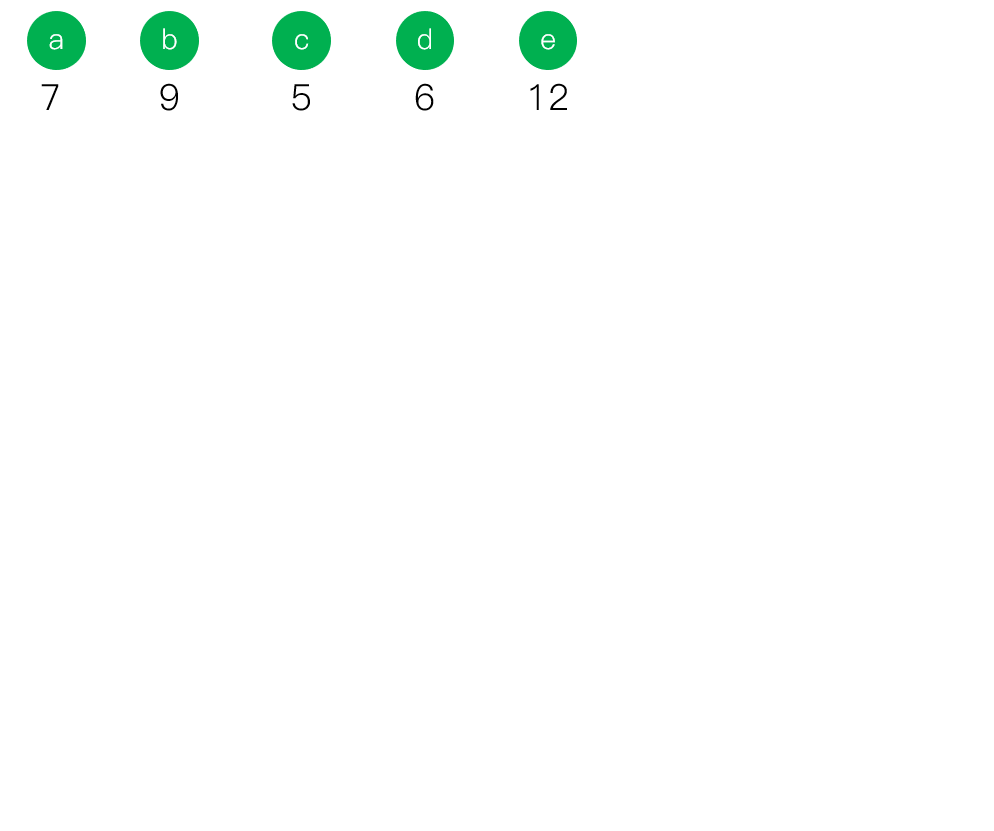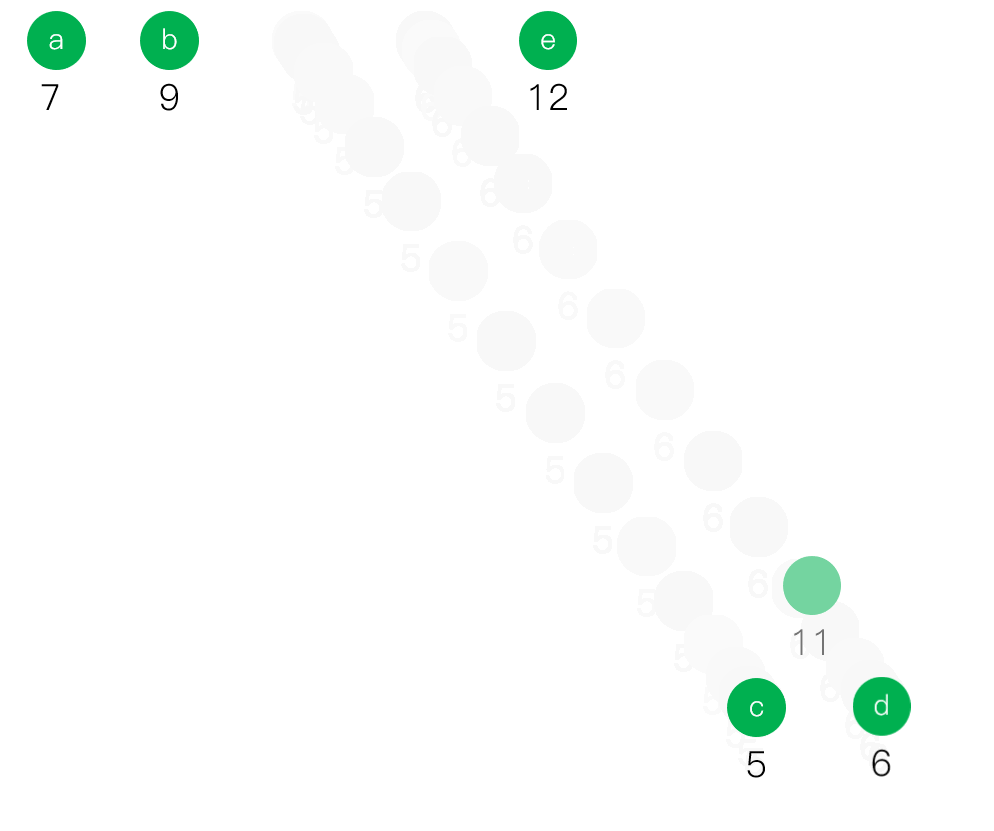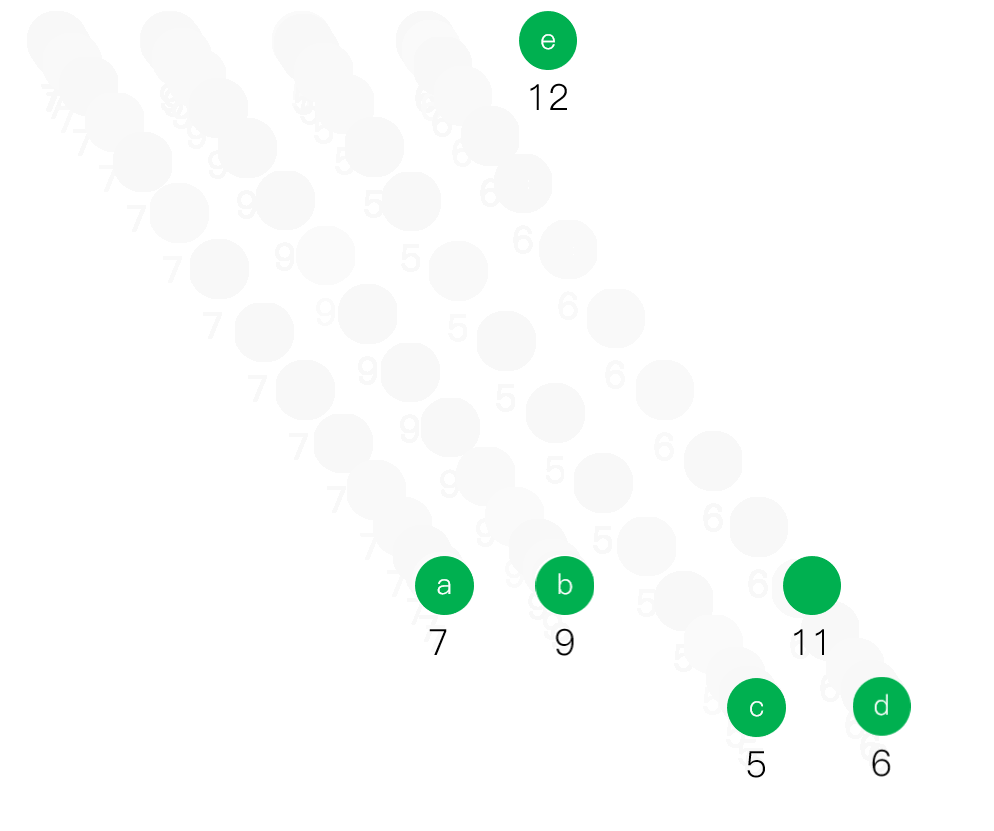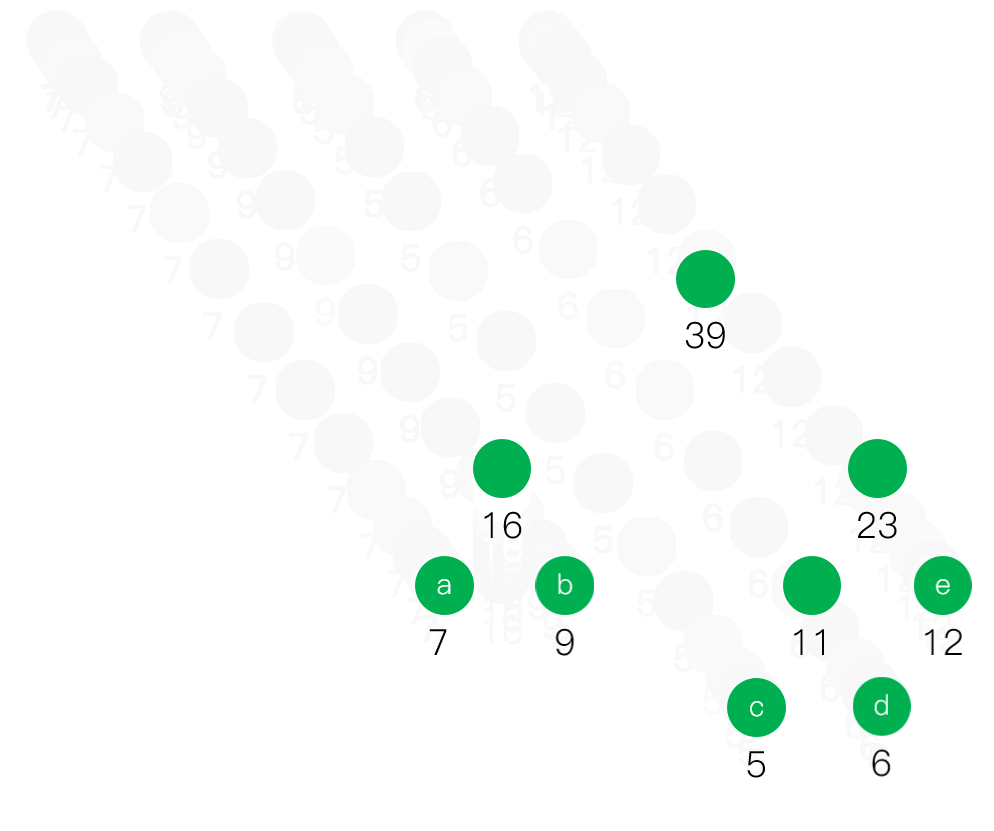
哈夫曼編碼
哈夫曼編碼比較簡單,就是將某棵二叉樹中每個結點的左分支標誌“0”,右分支標誌“1”,這樣,從根到每個葉結點形成“0”/“1”序列,將該序列作為葉結點對應字元的編碼,由此得到的二進位編碼稱為哈夫曼編碼。
請讀題
設某通訊系統中一個待傳輸的文本有6個不同字元,它們的出現頻率分別是0.5,0.8,1.4,2.2,2.3,2.8,試設計哈夫曼編碼
教材中給出了樹和哈夫曼編碼,直接看一下即可
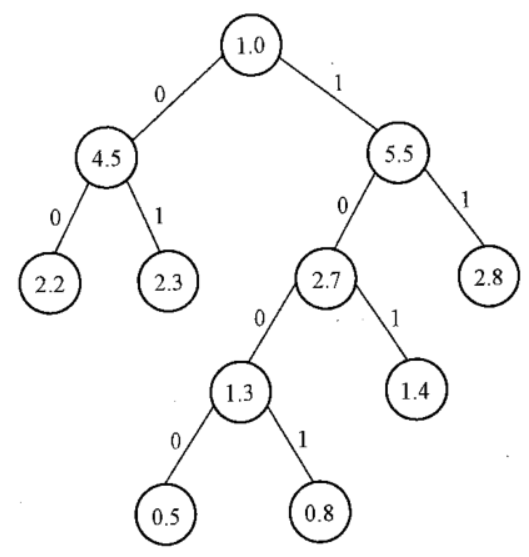
出現頻率為0.5的字元編碼為1000
出現頻率為0.8的字元編碼為1001
出現頻率為1.4的字元編碼為101
出現頻率為2.2的字元編碼為00
出現頻率為2.3的字元編碼為01
出現頻率為2.8的字元編碼為11
小結
樹形結構的應用非常廣泛,判定樹和哈夫曼樹可分別用於求解分類問題和有效分類問題以及哈夫曼編碼,哈夫曼編碼演算法的關鍵點是:每次合併具有最小權值和次小權值的兩個根結點,直到只剩下一個根結點為止。
對哈夫曼樹的每個結點的左分支和右分支分別置“0”或“1”,就可得到哈夫曼編碼。


