0.關於

        動態規劃是編程解題的一種重要手段。1951 年美國數學家 R.Bellman 等人，根據一類多階段問題的特點，把多階段決策問題變換為一系列互相聯繫的單階段問題，然後逐個加以解決。與此同時，他提出瞭解決這類問題的“最優化原理”，從而創建瞭解決最優化問題的一種新方法：動態規劃。
        動態規划算法通常用於求解具有某種最優性質的問題。在這類問題中，可能會有許多可行解。每一個解都對應於一個值，我們希望找到具有最優值的解。
        我們可以用一個表來記錄所有已解的子問題的答案。不管該子問題以後是否被用到，只要它被計算過，就將其結果填入表中。這就是動態規劃法的基本思路。具體的動態規划算法多種多樣，但它們具有相同的填表格式。

1.基本概念

        · 階段：把所給問題的求解過程恰當地分成若幹個相互聯繫的階段，以便於求解。過程不同，階段數就可能不同。描述階段的變數稱為階段變數，常用 k 表示。階段的劃分，一般是根據時間和空間的自然特征來劃分，但要便於把問題的過程轉化為多階段決策的過程。
        · 狀態：狀態表示每個階段開始面臨的自然狀況或客觀條件，它不以人們的主觀意志為轉移，也稱為不可控因素。通常一個階段有若幹個狀態，狀態通常可以用一個或一組數來描述，稱為狀態變數。
        · 決策：表示當過程處於某一階段的某個狀態時，可以做出不同的決定，從而確定下一階段的狀態，這種決定稱為決策。不同的決策對應著不同的數值，描述決策的變數稱決策變數。
        · 狀態轉移方程：動態規劃中本階段的狀態往往是上一階段的狀態和上一階段的決策的結果，由第 i 段的狀態 f(i) ,和決策 u(i) 來確定第 i+1 段的狀態。狀態轉移表示為 F(i+1) = T(f(i),u(i)) ，稱為狀態轉移方程。
        · 策略：各個階段決策確定後，整個問題的決策序列就構成了一個策略，對每個實際問題，可供選擇的策略有一定範圍，稱為允許策略集合。允許策略集合中達到最優效果的策略稱為最優策略。

動態規劃必須滿足最優化原理與無後效性。

        · 最優化原理：“一個過程的最優決策具有這樣的性質：即無論其初始狀態和初始決策如何，其今後諸策略對以第一個決策所形成的狀態作為初始狀態的過程而言，必須構成最優策略”。也就是說一個最優策略的子策略，也是最優的。
        · 無後效性：如果某階段狀態給定後，則在這個階段以後過程的發展不受這個階段以前各個狀態的影響。

舉個慄子

來看一道題目。

可憐的可樂機要回家，已知小可樂機在 左下角 (1,1) 位置，家在 右上角 (n,n) 坐標處。小可樂機走上一個格子 (i,j) 會花費一定的體力 a[i][j]，而且小可樂機只會往家的方向走，也就是只能往上，或者往右走。小可樂機想知道他回到家需要花費的最少體力是多少, 求你幫幫小可樂機吧qwq

例如下圖所示，格子中的數字代表走上該格子花費的體力：

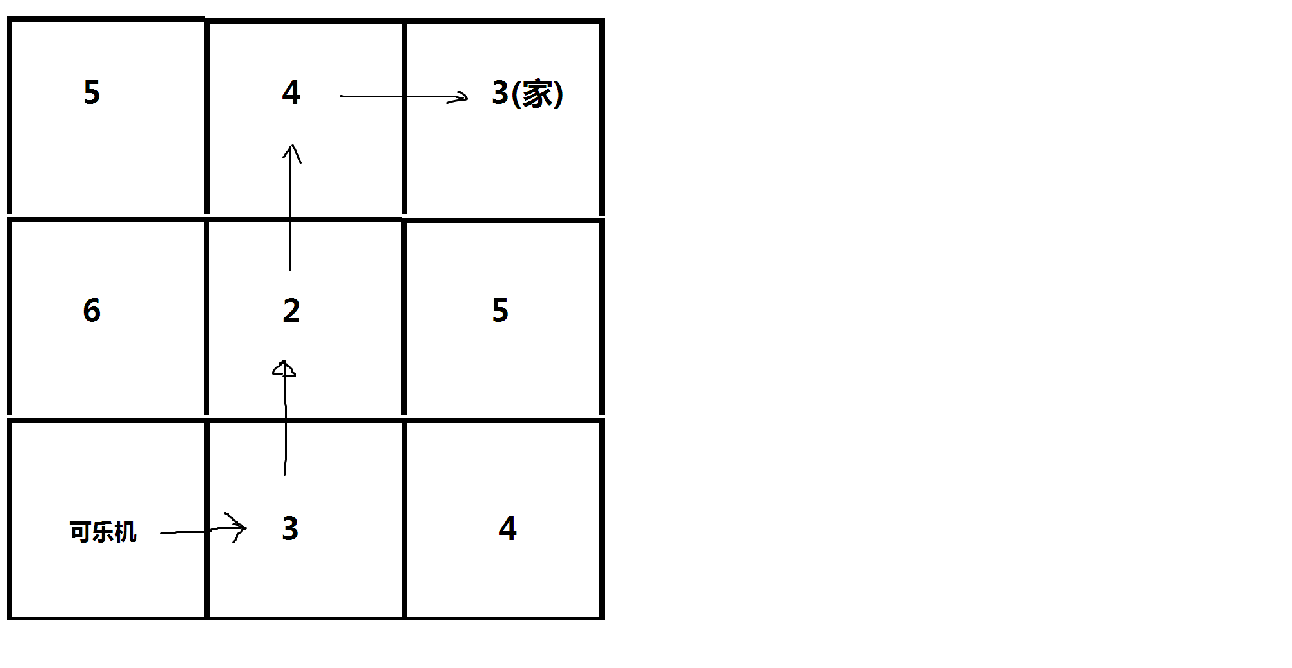
對於該圖來說，最優策略已在圖上標出，最少花費體力為：3 + 2 + 4 + 3 = 123 + 2 + 4 + 3 = 12。

我們把走到一個點看做一個狀態，對小可樂機來說，走到一個點只有兩種方式，一個是從下麵走到該點，一種是從左邊走到該點。那麼點 (i,j) 要麼是從 (i-1,j) 走到 (i,j)，要麼是從點 (i,j-1) 走到 (i,j)。

所以從哪個點走到 (i,j) 就是一個 決策。接下來，我們用 dp(i,j) 來代表走到點 (i,j) 一共花費的最少體力。
我們需要花費最少力氣走到家，所以可以得到狀態轉移方程：dp(i,j) = min(dp(i-1,j), dp(i,j-1)) + a[i][j] 。根據轉移方程，我們可以推出走到每個點花費的最少體力。

對於圖中的邊界點，要在轉移前加上判斷是否為邊界，如：點 (1,3) 只能從點 (1,2) 走過來，點 (3,1) 只能從點 (2,1) 走過來等等。

動態規劃的題目的核心是寫出狀態轉移方程，對於一個動態規劃的題目，如果我們能寫出轉移方程那麼代碼實現就變得簡單多了。大部分的動態規劃題目，在計算出轉移方程後，可以用類似於遞推的迴圈結構，來寫出代碼。

主要代碼

int a[100][100]; // a數組代表在點(i,j)花費的體力
int dp[100][100]; // dp數組代表走到點(i,j)一共花費的最少體力
dp[1][1] = 0;
for (int i = 1; i <= n; i++) 
{
    for (int j = 1; j <= n; j++)
    {
        if (i == 1 && j == 1) 
        {
            continue;
        } 
        else if (i == 1) //邊界點
        { 
            dp[i][j] = dp[i][j-1] + a[i][j];
        } 
        else if (j == 1)  //邊界點
        {
            dp[i][j] = dp[i-1][j] + a[i][j];
        } 
        else 
        {
            dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + a[i][j]; //轉移方程
        }
    }
}