本文中 $n$ 代表著待排序序列的長度。 演算法是否穩定:若 $a_i = a_j \ , \ i 1; merge(l,mid),merge(mid+1,r); mergesort(l,r,mid);return;//遞歸,先給小區間排序後大區間。 } merge(1,n); 上張圖理解一下: 可用 ...
- 本文中 \(n\) 代表著待排序序列的長度。
- 演算法是否穩定:若 \(a_i = a_j \ , \ i < j\),排序後若\(i < j\) 則穩定,反之不穩定。(可能有點歧義湊活看)
歸併排序
用了二分的思想。
在遞歸的過程中不斷將需要排序的區間縮小,使小區間有序後,再使大區間變得有序會簡單很多。
最差時間複雜度:\(O(nlogn)\)
最優時間複雜度:\(O(nlogn)\)
平均時間複雜度:\(O(nlogn)\)
演算法是否穩定:是
void mergesort(int l,int r,int mid) {//將[l,r]區間排好序
int i=l,j=mid+1,cnt=0;//[l,mid]與[mid+1,r]已經有序了,所以可以進行下麵的操作。
while(i<=mid&&j<=r) temp[++cnt]=a[i]<=a[j]?a[i++]:a[j++];
while(i<=mid) temp[++cnt]=a[i++];
while(j<=r) temp[++cnt]=a[j++];
for(int i=l;i<=r;++i) a[i]=temp[i-l+1];
}
void merge(int l,int r) {//不斷將區間縮小
if(l==r) return;
int mid=(l+r)>>1;
merge(l,mid),merge(mid+1,r);
mergesort(l,r,mid);return;//遞歸,先給小區間排序後大區間。
}
merge(1,n);上張圖理解一下: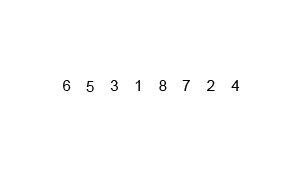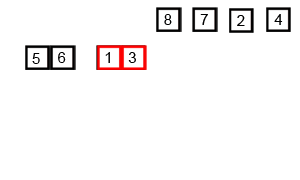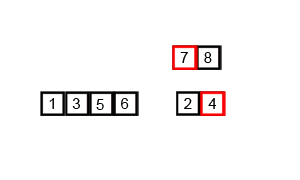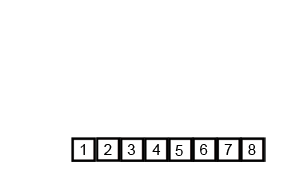
可用於求逆序對的個數。
堆排序
不想寫,咕咕咕。



