從2-3-4樹模型到紅黑樹實現

来源:https://www.cnblogs.com/jfire/archive/2019/12/01/11965377.html
-Advertisement-
Play Games

從2 3 4樹模型到紅黑樹實現 [TOC] 前言 紅黑樹，是一個高效的二叉查找樹。其定義特性保證了樹的路徑長度在黑色節點上完美平衡，使得其查找效率接近於完美平衡的二叉樹。 但是紅黑樹的實現邏輯很複雜，各種旋轉，顏色變化，直接針對其分析，大多數都是死記硬背各種例子，不太容易有個直觀的理解。實際上，紅黑 ...


目錄

從2-3-4樹模型到紅黑樹實現

前言

紅黑樹，是一個高效的二叉查找樹。其定義特性保證了樹的路徑長度在黑色節點上完美平衡，使得其查找效率接近於完美平衡的二叉樹。

但是紅黑樹的實現邏輯很複雜，各種旋轉，顏色變化，直接針對其分析，大多數都是死記硬背各種例子，不太容易有個直觀的理解。實際上，紅黑樹是實現手段，是其他概念模型為了方便在二叉樹上實現進而定義的節點顏色這個信息。如果從概念模型入手，再一一對應，就容易理解的多了。而紅黑樹能夠對應的模型有2-3樹，2-3-4樹等，下麵我們會以2-3-4樹作為概念模型，對紅黑樹進行分析。

2-3-4樹

2-3-4樹是對完美平衡二叉樹的擴展，其定義為：

  • 在一個節點中，可以存在1-3個key。
  • 2-節點，擁有1個key和2個子節點。
  • 3-節點，擁有2個key和3個子節點。
  • 4-節點，擁有3個key和4個子節點。
  • 子節點為空的節點稱為葉子節點。
  • 任意從根節點到葉子節點的路徑擁有相同的長度，即路徑上的鏈接數相同。

下圖就是一個2-3-4樹：

查找

2-3-4樹的查找很簡單，類似於二叉樹，步驟如下：

  • 將查找key和節點內的key逐一對比。
  • 如果命中，則返回節點內key的對應值。
  • 如果節點內的key都不命中，則沿著合適的鏈接到下一節點重覆該過程直到找到或者無後續節點。

舉個例子，如果我們要在上面的2-3-4樹中查詢11，其步驟如下：

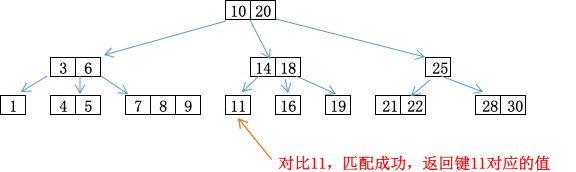
插入

2-3-4樹的插入，不會發生在中間節點，只會在葉子節點上進行插入。

、

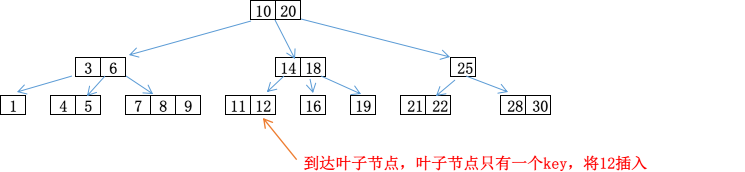
在葉子節點上新增key，會使得2-節點變為3-節點，3-節點變為4-節點。而原本的4-節點就沒有空間可以插入key了。為瞭解決這個問題，可以將4-節點中間的key推送給其父節點，剩下的2個key形成2個2-節點。效果如下

通過將4-的葉子節點拆分，產生了新的葉子節點可供key插入，同時將中間key送入父節點。該操作不會破壞樹的平衡性和高度。但如果葉子節點的父節點也是4-節點，這個操作就無法進行了。為瞭解決這個問題，有兩種思路：

  • 自底向上，從4-葉子節點開始分裂，如果分類後其父節點也是4-節點，繼續向上分裂，直到到達根節點。如果根節點也是4-節點，分裂後樹的高度+1。
  • 自頂向下，從根節點到插入所在的葉子節點路徑上，遇到4-節點就將其分裂。

兩種方法都能解決問題，不過自頂向下不需要遞歸，實現起來更簡單。通過這種處理方式，確保了1）最後到達的葉子節點必然是2-或者3-節點，搜索路徑上不存在4-節點。

樹的生長

2-3-4樹是向上生長的。這句話可以從根節點的分裂理解：如果根節點是一個4-節點，當新增key時，根節點會分裂，將中間的key推入父節點。根節點沒有父節點，因此中間的key就會成為新的根節點。如下所示：

整顆樹的生長可以看成是葉子節點不斷的新增key，並且在成為4-節點後被下一次的新增動作分解為2個2-節點，同時將一個key送入父節點。隨著這個過程的不斷進行，不斷有key從葉子節點向根節點匯聚，直到根節點成為4-節點併在下一次新增時被分類，進而讓樹升高1。

刪除

刪除是整個操作中最為複雜的部分，因為刪除可能發生在任意節點上，並且刪除後可能破壞2-3-4樹的完美平衡。在這裡，我們先來處理一些簡單的情況，最後再思考可以推而廣之的策略。

刪除最大key

在2-3-4樹中，刪除最大key必然是最右邊的葉子節點上。如果葉子節點是3-節點或者4-節點，只需要將其中最大的key刪除即可，不會對樹的平衡性造成影響。但如果刪除的key在2-節點上，情況就變得麻煩，因為刪除2-節點，導致樹的平衡被破壞。為了避免這個情況的發生，不能讓刪除發生在2-節點上。

為了讓刪除不落在2-節點上，可以將2-類型的葉子節點（最終要刪除的那個），從其兄弟節點“借”一個key進行融合變成3-節點；也可以將父節點的key和兄弟節點的key融合，變成一個4-節點，主要保證變化過程中樹的平衡性不被破壞即可。變換完成之後的節點類型是3-或4-，自然就可以成功刪除了。變化的可能情況有：

變化的策略是：

  1. 將父節點的key，自身的key，兄弟節點的key的合併後形成一個邏輯節點。
  2. 變化一：新節點為4-節點的情況下，父節點還有key，則新節點替換目標節點；
  3. 變化二：新節點為5-節點的情況下，最小key還給兄弟節點，次小key還給父節點，剩餘2個key設置到目標節點。
  4. 變化三：新節點為6-節點的情況下，最小key還給兄弟節點，次小key還給父節點，剩餘3個key設置到目標節點。

向下的搜索，最終達到需要刪除key的葉子節點。葉子節點的兄弟節點無法控制，而如果能保證目標key所在的葉子節點的父節點不是2-節點，就可以安全刪除key而不會破壞樹的結構。因此，在自頂向下的過程中，非根節點如果為2-節點，則通過變化成為非2-節點。這個轉化，僅僅針對搜索路徑的下一個節點而言，因此可能出現節點1被轉化為非2-節點後，其子節點是2-節點，子節點轉化為非2-節點時將父節點（節點1）恢覆成2-節點。轉化的最終目的是為了保證葉子節點的父節點是非2-節點即可，只不過為了達成這個保證，整個轉化行為需要從根節點一直進行下去。因此如果在葉子節點的時候執行轉化可能會導致子樹高度減1，這種變化會影響到全局樹的平衡。就需要迴圈向上迭代到根節點，比較複雜。而從根節點開始一路轉化下去，則容易理解和實現，也不會影響樹的平衡。

通過執行這種變化，在葉子節點中，就可以安全刪除key。

刪除最小key

最小key的刪除思路和操作方式和刪除最大key相似，只不過搜索路徑的方向是最左而已，其節點變化策略也是相似的，具體的變化有以下幾種：

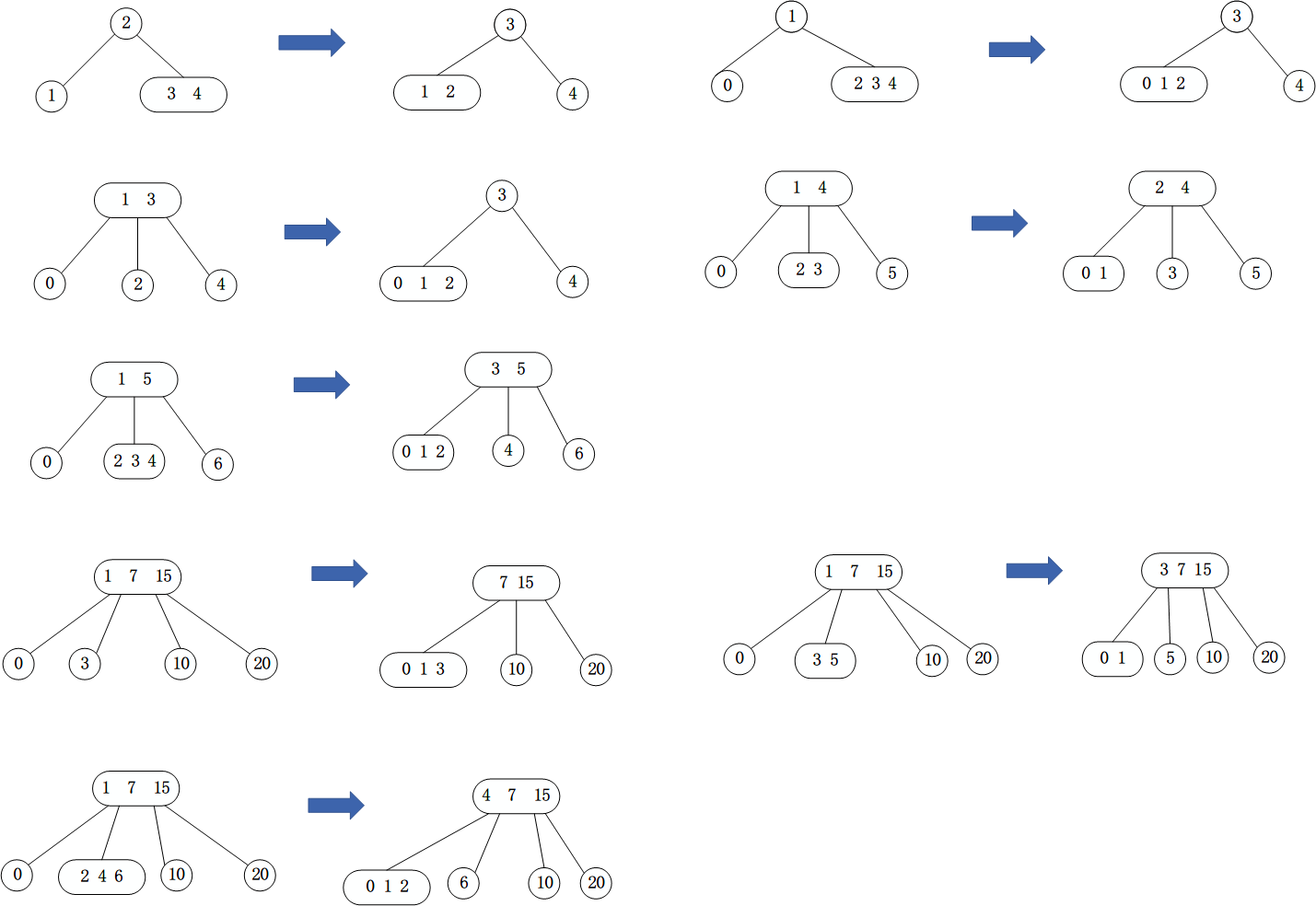
變化的策略是：

  1. 將父節點的key，自身的key，兄弟節點的key的合併後形成一個邏輯節點。
  2. 變化一：新節點為4-節點的情況下，父節點還有key，則新節點替換目標節點；
  3. 變化二：新節點為5-節點的情況下，最大key還給兄弟節點，次大key還給父節點，剩餘2個key設置到目標節點。
  4. 變化三：新節點為6-節點的情況下，最大key還給兄弟節點，次大key還給父節點，剩餘3個key設置到目標節點。

刪除任意key

刪除任一key就變得比較麻煩，key可能出現在中間節點上，刪除的話，樹的結構就被破壞了。這裡，我們可以採用一個取巧的思路：如果刪除的key是樹的中間節點，將該key替換為其中序遍歷的後繼key；該後繼key是刪除key的節點的右子樹的最小key。

key的替換對樹無影響；而將替換key刪除，則轉換為刪除對應子樹最小Key的問。刪除最小Key，需要從根節點自頂向下變化2-節點才能保證葉子節點中key的成功刪除。因此，刪除任一Key的具體處理思路可以總結為：

  1. 從根節點開始自頂向下搜索，非根節點如果為2-節點，則通過變化成為非2-節點。
  2. 搜索發現目標key，將其替換為中序搜索後繼key。
  3. 刪除步驟2節點的右子樹最小key。

左傾紅黑樹

2-3-4樹是一種概念模型，直接按照這個概念模型用代碼實現則比較複雜，主要的複雜有：

  • 維持3種節點類型。
  • 多種節點類型之間需要互相轉換。
  • 在樹中移動需要進行多次比較，如果節點不是2-節點的話。

因此在表現形式上，我們將2-3-4樹換另外一種形式來展現，進行以下變換：

  • 將2-3-4樹用二叉樹的形式表現。
  • 節點之間的鏈接區分為紅色和黑色。紅色鏈接用於將節點鏈接起來視作3-節點和4-節點。

這種轉換的關鍵點在於：

  • 轉換後的二叉樹可以使用二叉樹的搜索方式。
  • 轉換後的二叉樹和2-3-4樹處於一致關係，改變的只是表現形式。

不過由於3-節點兩種表現形式，增大了複雜性，因此對變換要求增加一條：紅色鏈接只能為左連接。通過三個約束後，轉換得到二叉樹我們稱之為左傾斜紅黑樹，其關鍵特性有：

  • 可以使用二叉樹搜索方式。
  • 與2-3-4樹保持一一對應。
  • 紅黑樹是黑色鏈接完美平衡的，也就是從根節點到葉子節點的任意路徑上，黑色鏈接的數量一致。

其對應方式如下：

可以看到，如果將紅色鏈接放平，就和2-3-4樹在展現上一致了。2-3-4樹是完美平衡的，其對應的左傾斜紅黑樹是黑色鏈接完美平衡，因為紅色鏈接是用於3-節點和4-節點的；而黑色鏈接就對應2-3-4樹中的鏈接。

左傾斜紅黑樹的轉換中不允許2種形式：

  • 右傾斜的紅色鏈接。
  • 兩個連續的紅鏈接在一個搜索路徑中（從根到葉子節點的路徑）

形象的說以下幾種不允許：

禁止的情況，減少了需要考慮的情形，為後續的編碼實現降低了難度。對於上述定義的左傾斜紅黑樹，使用數據結構來表達的話，在原本的二叉樹的節點中，增加一個屬性color，用於表示指向該節點的鏈接的顏色。

public class RedBlackTree
{
    private static final boolean RED   = true;
    private static final boolean BLACK = false;

    private       Node root;            // root of the BST
    private       int  heightBLACK;      // black height of tree

    private class Node
    {
        `key`   `key`;                  // `key`
        Value value;              // associated data
        Node  left, right;         // left and right subtrees
        boolean color;            // color of parent link
        private int    N;            // number of nodes in tree rooted here
        private int    height;       // height of tree rooted here

        Node(`key` `key`, Value value)
        {
            this.`key` = `key`;
            this.value = value;
            this.color = RED;
            this.N = 1;
            this.height = 1;
        }
    }
}

查找

紅黑樹的查找和二叉樹的一致，但是會更加快速，因為紅黑樹是黑色平衡的，搜索長度得到了控制。

插入

在介紹插入實現之前，首先要介紹紅黑樹中的兩種旋轉操作：

  • 右旋：將一個左傾斜的紅鏈接轉化為右鏈接。
  • 左旋：將一個右傾斜的紅鏈接轉化為左連接。

這兩個操作的重要性在於其變化是局部的，不影響黑色連接的平衡性。其變化如下：

紅黑樹的插入和二叉樹插入是相同的，只不過新增的鏈接是紅色的。因為紅黑樹的概念模型是2-3-4樹，2-3-4樹新增節點是在葉子節點上，並且新增後必然成為3-節點或者4-節點，所以新增鏈接均為紅色。

在新增完畢後，根據紅鏈接具體情況，進行旋轉處理，以保持左傾斜紅黑樹的要求。可能出現的情況有：

  • 在2-節點上新增key，表現在紅黑樹上，就是一個黑色的節點新增左連接或者右連接
  • 在3-節點上新增key，表現在紅黑樹上，就是被紅鏈接相連的兩個節點上3個可新增連接的地方新增紅鏈接。

2-節點的情況如下所示：

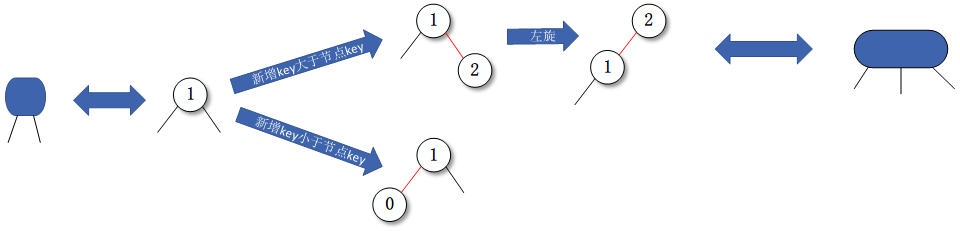
3-節點的情況如下所示：

左旋和右旋的方法如下：

private Node rotateLeft(Node h)//將節點的右紅鏈接轉化為左鏈接，並且返回原本節點的子樹轉化後新的子樹的根節點
    {
        Node x = h.right;
        h.right = x.left;
        x.left = setN(h);
        x.color = x.left.color;
        x.left.color = RED;
        return setN(x);//該方法用於計算節點x的子樹內的節點數量以及高度
    }

    private Node rotateRight(Node h)//將節點的左紅鏈接轉化為右鏈接，並且返回原本節點的子樹轉化後新的子樹的根節點
    {
        Node x = h.left;
        h.left = x.right;
        x.right = setN(h);
        x.color = x.right.color;
        x.right.color = RED;
        return setN(x);
    }

在2-3-4樹的節點插入中，為了避免葉子節點是4-節點導致沒有空間插入，所以從根節點到葉子節點的搜索路徑中，採用自頂向下的4-節點分解策略。而在紅黑樹中，對4-節點的分解動作是通過對節點的顏色變化完成的，如下圖所示：

翻轉的過程很簡單，就是將節點，節點的左右孩子節點的顏色都進行調整即可，顏色翻轉的代碼如下

private void colorFlip(Node h)
    {
        h.color = !h.color;
        h.left.color = !h.left.color;
        h.right.color = !h.right.color;
    }

4-節點的分解帶來的效果是將紅色鏈接向上層移動，這個移動可能產生一個紅色的右鏈接，此時需要通過左旋來修正；或者產生2個連續的紅鏈接，此時需要將其右旋，形成一個符合定義的4-節點。

總結來說，插入的過程首先是自頂向下，遇到4-節點就進行分解，直到到達葉子節點插入新的key；由於向下過程的4-節點可能產生右傾斜的紅鏈接，或者連續的2個紅鏈接，因此需要從葉子節點處向上到達根節點，修複產生的這些問題。處理方式主要是：

  • 右傾斜的紅鏈接左旋。
  • 連續的紅鏈接，通過右旋來達到符合定義的4-節點。

按照上述的總結，我們可以將新增節點的方法實現為

private Node insert(Node h, `key` `key`, Value value)//將KV對插入以h節點為根節點的樹，並且返回插入後該樹的根節點
    {
        if (h == null)//尋找到空白鏈接，返回新的節點。該節點為紅色鏈接指向的節點。
        {
            return new Node(`key`, value);
        }
        if (isRed(h.left) && isRed(h.right))//自頂向下的過程中，分裂4-節點。
        {
            colorFlip(h);
        }
        if (eq(`key`, h.`key`))
        {
            h.value = value;
        }
        else if (less(`key`, h.`key`))
        {
            h.left = insert(h.left, `key`, value);
        }
        else
        {
            h.right = insert(h.right, `key`, value);
        }
        if (isRed(h.right))//右傾斜的紅色鏈接，進行左旋。
        {
            h = rotateLeft(h);
        }
        if (isRed(h.left) && isRed(h.left.left))//連續的紅色鏈接，右旋變化為符合定義的4-節點
        {
            h = rotateRight(h);
        }
        return setN(h);
    }

刪除

和概念模型相同的方法，我們首先嘗試實現刪除最大key和刪除最小key，之後通過替換key位置來實現刪除任意Key功能。

刪除最大Key

和概念模型相同，刪除要發生在非2-節點上才能保證樹的平衡不被破壞。這就意味著刪除一定要發生在一個被紅色鏈接相連的節點上。概念模型當中，在自頂向下搜索過程需要保證中間節點不是2-節點來使得葉子節點必然可以轉化為非2-節點進行安全刪除；反應在紅黑樹中，搜索路徑的下一個節點，必須要被紅色鏈接相連。如果不是的話，則要進行變化，具體的手段包括：

  • 當前節點有左傾斜紅色鏈接時，將其進行右旋。右旋可以從概念模型上理解，可以認為搜索路徑是進行到3-節點或4-節點，並且從小key搜索到大key。
  • 搜索路徑的下一節點為2-節點，轉化為非-2節點。這個轉化過程，參考概念模型中的做法，將當前節點的key，右子節點的key，左子節點的key先合併，產生紅鏈接相連的邏輯節點。之後按照概念模型的拆分方式進行拆分。

針對步驟二，我們做下具體的分析。

當前節點不是2-節點，且3-節點的紅色左連接被轉化為右鏈接，因此在下一個節點為2-節點的情況下，當前節點必然是被右傾斜紅鏈接指向。所示初始狀態可能如下：

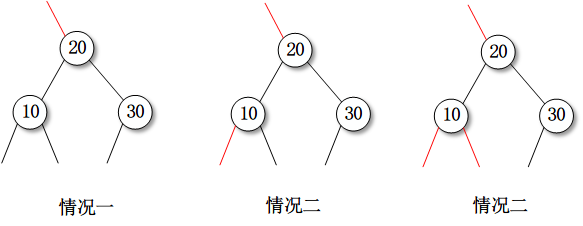
對於情況一，我們只需要對節點20進行顏色翻轉，就可以讓其後繼節點變為紅色，也就是鏈接變紅，即可。這種轉換對應概念模型中的變化1。

對於情況二，比較複雜。首先我們需要對節點20進行顏色翻轉。此時節點10和20在一行路徑上，對節點20的左連接右旋，右旋之後節點10變為新的根節點，對齊進行顏色翻轉。整個過程如下

這種轉換對應概念模型中的變化2。

情況三和情況二可以採用完全相同的變化步驟，轉換方式對應概念模型中的變化3。如下圖所示：

綜合情況一、二、三，我們可以將變換的代碼撰寫為

private Node moveRedRight(Node h)
    {
        colorFlip(h);//先翻轉
        if (isRed(h.left.left))//此時為情況二或者三
        {
            h = rotateRight(h);
            colorFlip(h);
        }
        return h;
    }

結合紅鏈接右旋和轉換2-節點，我們可以將刪除最大key的代碼編寫如下：

public void deleteMax()
    {
        root = deleteMax(root);
        root.color = BLACK;//如果根節點右子節點為2-節點，翻轉root節點會導致其顏色變紅，不符合定義。因此刪除完成後，將顏色恢復為顏色。
    }
private Node deleteMax(Node h)//刪除h節點為根節點的子樹中的最大節點，並且返回刪除後的子樹的根節點
    {
        if (isRed(h.left))
        {
            h = rotateRight(h);
        }
        if (h.right == null)//沒有右子樹了，刪除該節點
        {
            return null;
        }
        if (!isRed(h.right) && !isRed(h.right.left))//右子節點為2-節點，進行變化過程。
        {
            h = moveRedRight(h);
        }
        h.right = deleteMax(h.right);
        return fixUp(h);
    }
    private Node fixUp(Node h) //修正可能存在的異常鏈接情況。
    {
        if (isRed(h.right))
        {
            h = rotateLeft(h);
        }
        if (isRed(h.left) && isRed(h.left.left))
        {
            h = rotateRight(h);
        }
        if (isRed(h.left) && isRed(h.right))
        {
            colorFlip(h);
        }
        return setN(h);
    }

這個實現中引入了一個之前未曾提到的方法fixUp。因為在刪除的過程自頂向下的變換會產生一些不符合定義的鏈接情況：比如右傾斜的紅鏈接，比如連續的紅鏈接。在刪除完畢後，需要沿著之前的搜索路徑，自底向上，進行異常鏈接修複。

刪除最小Key

刪除最小Key的思路和刪除最大Key的思路非常接近，只不過在於搜索的方向不同，是沿著左子節點一直向下搜索。相比於刪除最大Key，刪除最小Key在搜索路徑向下的過程中不需要對紅鏈接方向進行旋轉，當搜索路徑的下一節點存在2-節點時轉化為非2-節點。可能存在的初始情況如下圖：

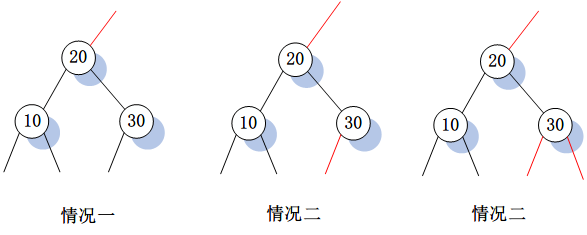
情況一很簡單，只需要對節點20進行顏色翻轉。該變換對應概念樹中的變化1。

對於情況二，先對節點20進行翻轉，再對節點30的左連接右旋，再對節點20的右鏈接左旋，最後對頂點進行翻轉。流程如下圖所示：

該變換對應概念模型中的變化2。

對於情況三則更複雜一些，其對應概念模型中的變化3，流程如下

和刪除最大key不同的地方在於情況三無法復用情況2的操作，否則會產生一個右傾斜的紅鏈接。不過即使是右傾斜紅鏈接，仍然是黑色平衡。但是與左傾斜紅黑樹定義不吻合，所以情況三使用了更多的步驟來產生符合定義的紅黑樹。

結合上述過程，我們可以將刪除最小Key的代碼編寫如下

public void deleteMin()
    {
        root = deleteMin(root);
        root.color = BLACK;
    }

    private Node deleteMin(Node h)
    {
        if (h.left == null)
        {
            return null;
        }
        if (!isRed(h.left) && !isRed(h.left.left))
        {
            h = moveRedLeft(h);
        }
        h.left = deleteMin(h.left);
        return fixUp(h);
    }
private Node moveRedLeft(Node h)
    {
        colorFlip(h);
        if (isRed(h.right.left))
        {
            if (isRed(h.right.right))
            {
                h.right = rotateRight(h.right);
                h = rotateLeft(h);
                h = rotateLeft(h);
                h.left = rotateRight(h.left);
                colorFlip(h);
            }
            else
            {
                h.right = rotateRight(h.right);
                h = rotateLeft(h);
                colorFlip(h);
            }

        }
        return h;
    }

刪除任意Key

和概念模型的刪除操作相似，自頂向下搜索，按照key的比較結果，可能向左右任意方向前進，如果下一步是一個2-節點，則參照刪除最大最小key中的變化方式進行變化。在確定key所在的節點後，將該key值替換為中序遍歷的後繼節點，繼而刪除該節點右子樹的最小節點。代碼如下

public void delete(Key key)
    {
        root = delete(root, key);
        root.color = BLACK;
}
 private Node delete(Node h, Key key)
    {
        if (less(key, h.key))
        {
            if (!isRed(h.left) && !isRed(h.left.left))
            {
                h = moveRedLeft(h);
            }
            h.left = delete(h.left, key);
        }
        else
        {
            if (isRed(h.left))
            {
                h = rotateRight(h);
            }
            if (eq(key, h.key) && (h.right == null))
            {
                return null;
            }
            if (!isRed(h.right) && !isRed(h.right.left))
            {
                h = moveRedRight(h);
            }
            if (eq(key, h.key))
            {
                h.value = get(h.right, min(h.right));
                h.key = min(h.right);
                h.right = deleteMin(h.right);
            }
            else
            {
                h.right = delete(h.right, key);
            }
        }
        return fixUp(h);
    }

總結

紅黑樹作為概念樹的實際實現，其代碼很複雜，要求的變化方式也很多。從概念樹的映射來說，2-3樹，2-3-4樹都可以映射到紅黑樹上。而左傾斜紅黑樹，使用遞歸方式實現的代碼，無疑是很好理解，代碼量也較少的。而JDK中TreeMap採用概念模型也是2-3-4樹，不過並不限制右傾斜。總體而言，紅黑樹有太多變種，瞭解其原理最為重要，實現上，能使用即可，深究的話，意義不大。

參考文獻

《Left-Leaning Red-Black Trees》（Princeton University）

文章原創首發於公眾號：林斌說Java，轉載請註明來源，謝謝。
更多高質量原創文章，歡迎掃碼關註


您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • 數據結構與演算法之演算法篇
    什麼是演算法？ 演算法是解決特定問題求解步驟的描述，在電腦中表現為指令的有限序列，並且每條指令表示一個或多個操作。 簡單來說，就是我們解決某一問題所使用的技巧和方法。 一個問題可以由多個演算法解決，一個演算法也不可能具有通解所有問題的能力。 演算法的特征： 輸入：演算法具有零個或多個輸入； 輸出：演算法至少有一 ...
  • html文本框預設值刷新後無法繼續顯示解決方法
    轉載於：https://blog.csdn.net/yufeitong/article/details/8485129 有這種情況，文本框輸入值後，再次刷新預設值就無法顯示了 原始html代碼： <form action="" method="post"> <input name="" type=" ...
  • CSS標準文檔流
    標準文檔流介紹 我們在製作 網頁的時候，都必須遵循一個 的規則如：從左至右、從上至下規則。 讓我們進入 網頁的標準文檔流基本原理實踐。 代碼塊 結果圖 標準文檔流要註意的事項 空白摺疊現象。 高矮不齊，底部對齊。 讓我們進入空白摺疊現象實踐。 代碼塊 結果圖 註意：咦結果圖之間怎麼有了空白的縫隙呢？ ...
  • 初步瞭解Node.js，學做簡單的留言本案例
    在還沒有正式的學Node.js的時候， 你們認為Node.js 對於前端來說是什麼呢？ 會認為Node.js 是框架？ 認為這是類似Jquery的一個快速、簡潔的JavaScript框架？ 反正我自己起初是這麼認為的，因為它後面有個 .js。 那麼在正式開始接觸Node.js的時候，才發現自己是有多 ...
  • 原生JS實現移動端輪播圖
    功能描述： 自動無縫輪播圖片，底部小圓點跟圖片保持一致；手指左右移動輪播圖，移動距離大於50px播放下一張（或上一張），小於50px則回彈 具體功能實現： 1.定時器 自動輪播圖片 先聲明一個index=0用來存圖片索引； 添加一個定時器，每隔兩秒調用一次，每調用一次定時器（圖片播放一次）index ...
  • CSS的三種樣式，有一種你肯定不知道
    前言本文的文字及圖片來源於網路,僅供學習、交流使用,不具有任何商業用途,版權歸原作者所有,如有問題請及時聯繫我們以作處理。作者LFuser 正文新手註意：如果你學習遇到問題找不到人解答，可以點我進裙，裡面大佬解答及web前端精講教.程！ CSS樣式分為：內聯式css樣式、嵌入式css樣式、外部式cs ...
  • javaweb 複習隨筆
    js和jsp區分: js是一種腳本語言，常運行在前臺和客戶端交互，不會給伺服器帶來負擔，可以更好的修飾靜態頁面 jsp可以說是servlet的一種，jsp會先翻譯，翻譯成Servlet執行，運行在伺服器上，可以處理html上的數據和顯示 總的來說還是有沒有和伺服器數據交互的區別，資料庫交互和圖像處理 ...
  • SSM 輕量級框架構建圖書管理系統
    一、大致效果展示圖 二、整體編碼思想 三、資料庫相關信息 SELECT * From books where ${param1} like '%${param2}%' order by createDate DESC limit ${param3},3 四、Maven 配置本地倉庫和阿裡公共包 se ...
一周排行
    -Advertisement-
    Play Games
  • Dapr Outbox 執行流程
    Dapr Outbox 是1.12中的功能。 本文只介紹Dapr Outbox 執行流程，Dapr Outbox基本用法請閱讀官方文檔 。本文中appID=order-processor，topic=orders 本文前提知識：熟悉Dapr狀態管理、Dapr發佈訂閱和Outbox 模式。 Outbo ...
  • Advanced .Net Debugging 7：托管堆與垃圾收集
    引言 在前幾章我們深度講解了單元測試和集成測試的基礎知識，這一章我們來講解一下代碼覆蓋率,代碼覆蓋率是單元測試運行的度量值,覆蓋率通常以百分比表示，用於衡量代碼被測試覆蓋的程度，幫助開發人員評估測試用例的質量和代碼的健壯性。常見的覆蓋率包括語句覆蓋率（Line Coverage）、分支覆蓋率（Bra ...
  • C#S7.NET實現西門子PLCDB塊數據採集的完整步驟
    前言 本文介紹瞭如何使用S7.NET庫實現對西門子PLC DB塊數據的讀寫，記錄了使用電腦模擬，模擬PLC，自至完成測試的詳細流程，並重點介紹了在這個過程中的易錯點，供參考。 用到的軟體： 1.Windows環境下鏈路層網路訪問的行業標準工具（WinPcap_4_1_3.exe）下載鏈接：http ...
  • WPF控制項：密碼框綁定MVVM
    從依賴倒置原則（Dependency Inversion Principle, DIP）到控制反轉（Inversion of Control, IoC）再到依賴註入（Dependency Injection, DI）的演進過程，我們可以理解為一種逐步抽象和解耦的設計思想。這種思想在C#等面向對象的編 ...
  • Python中的私有屬性與私有方法
    關於Python中的私有屬性和私有方法 Python對於類的成員沒有嚴格的訪問控制限制，這與其他面相對對象語言有區別。關於私有屬性和私有方法，有如下要點： 1、通常我們約定，兩個下劃線開頭的屬性是私有的（private）。其他為公共的（public）； 2、類內部可以訪問私有屬性（方法）； 3、類外 ...
  • C++ 訪問說明符詳解：封裝數據，控制訪問，提升安全性
    C++ 訪問說明符 訪問說明符是 C++ 中控制類成員（屬性和方法）可訪問性的關鍵字。它們用於封裝類數據並保護其免受意外修改或濫用。 三種訪問說明符： public：允許從類外部的任何地方訪問成員。 private：僅允許在類內部訪問成員。 protected：允許在類內部及其派生類中訪問成員。 示 ...
  • static_cast與dynamic_cast到底是什麼？
    寫這個隨筆說一下C++的static_cast和dynamic_cast用在子類與父類的指針轉換時的一些事宜。首先，【static_cast，dynamic_cast】【父類指針，子類指針】，兩兩一組，共有4種組合：用 static_cast 父類轉子類、用 static_cast 子類轉父類、使用 ...
  • C語言數據結構：雙向鏈表的增刪操作
    /******************************************************************************************************** * * * 設計雙向鏈表的介面 * * * * Copyright (c) 2023-2 ...
  • @ComponentScan註解的實現，Spring掃描包的過程
    相信接觸過spring做開發的小伙伴們一定使用過@ComponentScan註解 @ComponentScan("com.wangm.lifecycle") public class AppConfig { } @ComponentScan指定basePackage，將包下的類按照一定規則註冊成Be ...
  • opensips開啟python支持
    操作系統 ：CentOS 7.6_x64 opensips版本： 2.4.9 python版本：2.7.5 python作為腳本語言，使用起來很方便，查了下opensips的文檔，支持使用python腳本寫邏輯代碼。今天整理下CentOS7環境下opensips2.4.9的python模塊筆記及使用 ...
所有分類