A いっしょ / Be Together (結論/暴力) "題目鏈接" 題目大意: 有 $n$ 個數字,要將它們變成相等,對每一個數字最多操作一次,如將 $a \to b$ 的代價為 $(a b)^2$ ,求出最小的代價。 大致思路: 根據不等式的知識可以知道,假設最後數字變為 $x$,那麼 $x$ ...
A - いっしょ / Be Together (結論/暴力)
題目大意:
有 \(n\) 個數字,要將它們變成相等,對每一個數字最多操作一次,如將 \(a \to b\) 的代價為 \((a-b)^2\) ,求出最小的代價。
大致思路:
根據不等式的知識可以知道,假設最後數字變為 \(x\),那麼 \(x\) 為 \(\sum{a_i}\) 平均數的代價最小,由於要為整數,就取最接近 \(x\) 兩個整數做為結果,取其中最小的代價就行了。
代碼:
#include<bits/stdc++.h>
using namespace std;
int n;
int a[200];
int main()
{
//freopen("H:\\c++1\\in.txt","r",stdin);
//freopen("H:\\c++1\\out.txt","w",stdout);
scanf("%d",&n);
int ans1=0,ans2=0,sum=0;
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
sum+=a[i];
}
int t1=sum/n,t2=(sum+n-1)/n;
for(int i=1;i<=n;i++){
ans1+=(t1-a[i])*(t1-a[i]);
ans2+=(t2-a[i])*(t2-a[i]);
}
printf("%d\n",min(ans1,ans2));
return 0;
}B - アンバランス / Unbalanced (思維)
題目大意:
給定一個字元串 \(s\) ,問其中是否存在“不平衡”的連續子串,“不平衡”的字元串被定義為長度大於等於 \(2\) ,且其中一個字母出現次數過半。有的話任意輸出一個。
大致思路:
一開始,想到要大於半數,那麼必須存在兩個相鄰的字母相同,交上去 \(wa\) 了,後來發現其實還有一種可能就是 \(3\) 個字母,頭尾相同,如 \(aba\) ,把兩種情況都枚舉一下,就行了。
代碼:
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
char s[N];
int main()
{
//freopen("H:\\c++1\\in.txt","r",stdin);
//freopen("H:\\c++1\\out.txt","w",stdout);
scanf("%s",s+1);
int len=strlen(s+1);
if(len==2&&s[1]==s[2]){ // 特判
printf("1 2\n");
return 0;
}
int l=-1,r=-1;
for(int i=1;i<len-1;i++){
if(s[i]==s[i+1]||s[i]==s[i+2]||s[i+1]==s[i+2]){
l=i,r=i+2;
break;
}
}
printf("%d %d\n",l,r);
return 0;
}C - キャンディーとN人の子供 / Children and Candie (dp+計算貢獻)
題目大意:
有 \(n\) 個人, \(C\) 個糖果,將 \(C\) 個糖果分配給 \(n\) 個人,每一個人有 \(c_i\) 個,可以為 \(0\) 個,每一個人有一個活躍度 \(x_i\) ,那麼這次分配的價值為 \(\prod{x_i^{c_i}}\) ,將一個值用 \(f(x_1,x_2,...,x_n)\) 表示,現在給你兩個數字 \(A[n],B[n]\) ,要求求出下式。
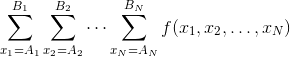
大致思路:
雖然這題過了,但是還是有很多細節的部分沒用弄懂,一開始根本沒有想到 \(dp\) 來解,後來看了題解才知道,當 \(A_i=B_i\) 的情形比較好想,設 \(dp[i] [j]\) 表示分給前i個人,使用 \(j\) 個糖果的價值數,那麼可以寫出方程,\(dp[i][j]+=dp[i-1][j-k]*(A_i^k)\) , \(k\) 其實就是枚舉分給第 \(i\) 個人的糖果,但是當 \(A_i != B_i\) 的時候,我對於為什麼可以將求和號提出來有些疑惑,就是為什麼可以單獨計算某一個對總體的貢獻。具體的解法就是,將上述方程改成 \(dp[i] [j] += dp[i-1] [j-k] * (\sum_{t=A[i]}^{B[i]}{t^k})\),然後通過預處理就可以 \(O(n^3)\) 的過了。
(之後還得在思考思考)
代碼:
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=500;
const int mod=1e9+7;
ll ksm(ll a,ll b){ // 快速冪
ll res=1,t=a;
while(b){
if(b&1)res=(res*t)%mod;
t=(t*t)%mod;
b>>=1;
}
return res;
}
ll dp[N][N];
ll n,c;
ll a[N],b[N];
ll p[N][N];
ll sum[N][N];
void init(){ // 預處理
for(int i=1;i<N;i++)
for(int j=0;j<N;j++)p[i][j]=ksm(i,j);
for(int k=0;k<N;k++){
for(int i=1;i<N;i++)sum[i][k]=(sum[i-1][k]+p[i][k])%mod;
}
}
int main()
{
//freopen("H:\\c++1\\in.txt","r",stdin);
//freopen("H:\\c++1\\out.txt","w",stdout);
init();
scanf("%lld%lld",&n,&c);
for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
for(int i=1;i<=n;i++)scanf("%lld",&b[i]);
dp[0][0]=1;
for(int i=1;i<=n;i++)
for(int j=0;j<=c;j++){
for(int k=0;k<=j;k++){ //枚舉第i個人拿的糖果數
dp[i][j]=(dp[i][j]+(dp[i-1][j-k]*(sum[b[i]][k]-sum[a[i]-1][k]+mod)%mod))%mod;
}
}
printf("%lld\n",dp[n][c]);
return 0;
}D - バイナリハック / Unhappy Hacking (dp計數)
題目大意:
有 \(3\) 個按鍵,分別是 \(,,0,1,backspace\) 鍵,按下 \(0\) 或者 \(1\) ,就會在最右邊出現 \(0\) 或者 \(1\) ,按下 \(backspace\) 鍵就會將最右邊的數字刪去,如果沒有數字就無事發生。現在告訴你一串數字,並且按了 \(n\) 次鍵,問有幾種按法。
大致思路:
這題一開始想分類討論,後來發現刪除的數字若是連在一起又可以改變刪除的順序就不會做了,看了題解,原來就是我一開始寫的 \(dp\) ,但是當時不懂怎麼轉移。用 \(dp[i][j]\) 表示按了 \(i\) 下,數字長度為 \(j\) 的方案數,我們考慮當前按下的是數字,那麼必然是和給定串的對應位相同,若按下的是刪除鍵,那麼就這位刪除的可以是 \(0\) 也可以是 \(1\) 就有兩種可能,按照這個轉移一下即可。
代碼:
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=5010;
const int mod=1e9+7;
ll dp[N][N];
char s[N];
int n;
int main()
{
//freopen("H:\\c++1\\in.txt","r",stdin);
//freopen("H:\\c++1\\out.txt","w",stdout);
dp[0][0]=1;
scanf("%d",&n);
scanf("%s",s+1);
int len=strlen(s+1);
for(int i=0;i<=n;i++)
for(int j=0;j<=n;j++){
if(j==0)dp[i+1][j]=(dp[i][j]+dp[i+1][j])%mod;//特判
else{
dp[i+1][j-1]=(dp[i][j]*2+dp[i+1][j-1])%mod;//按backspace
}
dp[i+1][j+1]=(dp[i+1][j+1]+dp[i][j])%mod;//按數字鍵
}
printf("%lld\n",dp[n][len]);
return 0;
}



