高德JS依賴分析工程及關鍵原理

一、背景

高德 App 進行 Bundle 化後，由於業務的複雜性，Bundle 的數量非常多。而這帶來了一個新的問題——Bundle 之間的依賴關係錯綜複雜，需要進行管控，使 Bundle 之間的依賴保持在架構設計之下。

並且，為了保證 Bundle 能實現獨立運轉，在業務持續迭代的過程中，需要逆向的依賴關係來迅速確定迭代的影響範圍。同時，對於切麵 API（即對容器提供的系統 API，類似瀏覽器中的 BOM API），也需要確定每個切麵 API 的影響範圍以及使用趨勢，來作為修改或下線某個 API 的依據。

以組件庫為例，由於組件會被若幹業務項目所使用，我們對組件的修改會影響這些業務項目。在計劃修改前，需要根據正向的依賴關係（業務依賴組件）來算出逆向的依賴關係——該組件被哪些地方所依賴，從而確定這個組件修改的影響範圍。

比文件更高的維度，是 Bundle 間的依賴。我們有業務 Bundle，也有公共 Bundle。公共 Bundle 也分為不同層級的 Bundle。

對於公用 Bundle，業務 Bundle 可以依賴它，但公用 Bundle 不能反過來依賴業務 Bundle；同樣的，底層的 Bundle 也禁止依賴上層封裝的 Bundle。我們需要通過依賴分析，來確保這些依賴按照上述規則進行設計。

二、實現關鍵步驟

實現 JS 依賴分析，整個實現過程大致如下圖所示：

下麵挑一些關鍵步驟來展開介紹。

使用 AST 提取依賴路徑

要做文件級別的依賴分析，就需要提取每個文件中的依賴路徑，提取依賴路徑有 2 個方法：

• 使用正則表達式，優點是方便實現，缺點是難以剔除註釋，靈活度也受限；
• 先進行詞法分析和語法分析，得到 AST（抽象語法樹）後，遍歷每個語法樹節點，此方案的優點是分析精確，缺點是實現起來要比純正則麻煩，如果對應語言沒有提供 parser API（如 Less），那就不好實現。

一般為了保證準確性，能用第 2 個方案的都會用第 2 個方案。

以類 JS（.js、.jsx、.ts、.tsx）文件為例，我們可以通過 TypeScript 提供的 API ts.createSourceFile 來對類 JS 文件進行詞法分析和語法分析，得到 AST：

const ast = ts.createSourceFile(
  abPath,
  content,
  ts.ScriptTarget.Latest,
  false,
  SCRIPT_KIND[path.extname(abPath)]
);

得到 AST 後，就可以開始遍歷 AST 找到所有我們需要的依賴路徑了。遍歷時，可以通過使用 typeScript 模塊提供的 ts.forEachChild 來遍歷一個語法樹節點的所有子節點，從而實現一個遍歷函數 walk：

function walk (node: ts.Node) {
  ts.forEachChild(node, walk); // 深度優先遍歷

  // 根據不同類型的語法樹節點，進行不同的處理
  // 目的是找到 import、require 和 require.resolve 中的路徑
  // 上面 3 種寫法分為兩類——import 聲明和函數調用表達式
  // 其中函數調用表達式又分為直接調用（require）和屬性調用（require.resolve）
  switch (node.kind) {
    // import 聲明處理
    case ts.SyntaxKind.ImportDeclaration:
      // 省略細節……
      break;

    // 函數調用表達式處理
    case ts.SyntaxKind.CallExpression:
      // 省略細節
      break;
  }
}

通過這種方式，我們就可以精確地找到類 JS 文件中所有直接引用的依賴文件了。

當然了，在 case 具體實現中，除了用戶顯式地寫依賴路徑的情況，用戶還有可能通過變數的方式動態地進行依賴載入，這種情況就需要進行基於上下文的語義分析，使得一些常量可以替換成字元串。

但並不是所有的動態依賴都有辦法提取到，比如如果這個動態依賴路徑是 Ajax 返回的，那就沒有辦法了。不過無需過度考慮這些情況，直接寫字元串字面量的方式已經能滿足絕大多數場景了，之後計劃通過流程管控+編譯器檢驗對這類寫法進行限制，同時在運行時進行收集報警，要求必需顯式引用，以 100% 確保對切麵 API 的引用是可以被靜態分析的。

建立文件地圖進行尋路

我們對於依賴路徑的寫法，有一套自己的規則：

引用類 JS 文件支持不寫擴展名；

引用本 Bundle 文件，可直接只寫文件名；

使用相對路徑；

引用公用 Bundle 文件，通過 @${bundleName}/${fileName} 的方式引用，fileName 同樣是直接只寫該 Bundle 內的文件名。

這些方式要比 CommonJS 或 ECMAScript Module 的規劃要稍複雜一些，尤其是「直接只寫文件名」這個規則。對於我們來說，需要找到這個文件對應的真實路徑，才能繼續進行依賴分析。

要實現這個，做法是先構建一個文件地圖，其數據結構為 { [fileName]: ‘relative/path/to/file’ } 。我使用了 glob 來得到整個 Bundle 目錄下的所有文件樹節點，篩選出所有文件節點，將文件名作為 key，相對於 Bundle 根目錄的路徑作為 value，生成文件地圖。在使用時，「直接只寫文件名」的情況就可以直接根據文件名以 O(1) 的時間複雜度找到對應的相對路徑。

此外，對於「引用類 JS 文件支持不寫擴展名」這個規則，需要遍歷每個可能的擴展名，對路徑進行補充後查找對應路徑，複雜度會高一些。

依賴是圖的關係，需先建節點後建關係

在最開始實現依賴關係時，由於作為前端的慣性思維，會認為「一個文件依賴另一些文件」是一個樹的關係，在數據結構上就會自然地使用類似文件樹中 children: Node[] 的方式——鏈式樹結構。而實際上，依賴是會出現這種情況的：

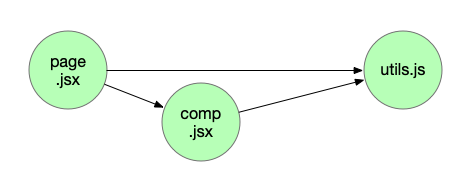
如果使用樹的方式來維護，那麼 utils.js 節點就會分別出現在 page.jsx 和 comp.jsx 的 children 中，出現冗餘數據，在實際項目中這種情況會非常多。

但如果僅僅是體積的問題，可能還沒那麼嚴重，頂多費點空間成本。但我們又會發現，文件依賴還會出現這種迴圈依賴情況：

寫 TypeScript 時在進行類型聲明的時候，就經常會有這樣迴圈依賴的情況。甚至兩個文件之間也會迴圈依賴。這是合理的寫法。

但是，這種寫法對於直接使用鏈式樹結構來說，如果創建鏈式樹的演算法是「在創建節點時，先創建子節點，待子節點創建返回後再完成自身的創建」的話，就不可能實現了，因為我們會發現，假如這樣寫就會出現無限依賴：

const fooTs = new Node({
  name: 'foo.ts',
  children: [
    new Node({ 
      name: 'bar.ts', 
      children: [
        new Node({
          name: 'baz.ts',
          children: [
            new Node({
              name: 'foo.ts', // 和最頂的 foo.ts 是同一個
              children: [...] // 無限迴圈……
            })
          ]
        })
      ]
    })
  ]
})

此問題的根本原因是，這個關係是圖的關係，而不是樹的關係，所以在創建這個數據結構時，不能使用「在創建節點時，先創建子節點，待子節點創建返回後再完成自身的創建」演算法，必須把思路切換回圖的思路——先創建節點，再創建關係。

採用這種做法後，就相當於使用的是圖的鄰接鏈表結構了。我們來看看換成「先創建節點，再創建關係」後的寫法：

// 先創建各節點，並且將 children 置為空數組
const fooTs = new Node({
  name: 'foo.ts',
  children: []
});

const barTs = new Node({
  name: 'bar.ts',
  children: []
});

const bazTs = new Node({
  name: 'baz.ts',
  children: []
});


// 然後再創建關係
fooTs.children.push(barTs);
barTs.children.push(bazTs);
bazTs.children.push(fooTs);

使用這種寫法，就可以完成圖的創建了。

但是，這種數據結構只能存在於記憶體當中，無法進行序列化，因為它是迴圈引用的。而無法進行序列化就意味著無法進行儲存或傳輸，只能在自己進程里玩這樣子，這顯然是不行的。

所以還需要對數據結構進行改造，將鄰接鏈表中的引用換成子指針表，也就是為每個節點添加一個索引，在 children 里使用索引來進行對應：

const graph = {
  nodes: [
    { id: 0, name: 'foo.ts', children: [1] },
    { id: 1, name: 'bar.ts', children: [2] },
    { id: 2, name: 'baz.ts', children: [0] }
  ]
}

這裡會有同學問：為什麼我們不直接用 nodes 的下標，而要再添加一個跟下標數字一樣的 id 欄位？原因很簡單，因為下標是依賴數組本身的順序的，如果一旦打亂了這個順序——比如使用 filter 過濾出一部分節點出來，那這些下標就會發生變化。而添加一個 id 欄位看起來有點冗餘，但卻為後面的演算法降低了很多複雜度，更加具備可擴展性。

用棧來解決迴圈引用（有環有向圖）的問題

當我們需要使用上面生成的這個依賴關係數據時，如果需要進行 DFS（深度遍歷）或 BFS（廣度遍歷）演算法進行遍歷，就會發現由於這個依賴關係是迴圈依賴的，所以這些遞歸遍歷演算法是會死迴圈的。要解決這個問題很簡單，有三個辦法：

• 在已有圖上添加一個欄位來進行標記

每次進入遍歷一個新節點時，先檢查之前是否遍歷過。但這種做法會污染這個圖。

• 創建一個新的同樣依賴關係的圖，在這個新圖中進行標記

這種做法雖然能實現，但比較麻煩，也浪費空間。

• 使用棧來記錄遍歷路徑

我們創建一個數組作為棧，用以下規則執行：

每遍歷一個節點，就往棧里壓入新節點的索引（push）；

每從一個節點中返回，則移除棧中的頂部索引（pop）；

每次進入新節點前，先檢測這個索引值是否已經在棧中存在（使用 includes），若存在則回退。

這種方式適用於 DFS 演算法。

三、總結

依賴關係是源代碼的另一種表達方式，也是把控巨型項目質量極為有利的工具。我們可以利用依賴關係挖掘出無數的想象空間，比如無用文件查找、版本間變動測試範圍精確化等場景。若結合 Android、iOS、C++ 等底層依賴關係，就可以計算出更多的分析結果。

目前，依賴關係掃描工程是迭代式進行的，我們採用敏捷開發模式，從一些簡單、粗略的 Bundle 級依賴關係，逐漸精確化到文件級甚至標識符級，在落地的過程中根據不同的精確度來逐漸滿足對精度要求不同的需求，使得整個過程都可獲得不同程度的收益和反饋，驅使我們不斷持續迭代和優化。