在分析jdk1.8的HashMap實現原理之前,咱們先可以瞭解一下紅黑樹的設計,相比jdk1.7的HashMap而言,jdk1.8最重要的就是引入了紅黑樹的設計,當衝突的鏈表長度超過8個的時候,鏈表結構就會轉為紅黑樹結構。 ...
一、故事的起因
JDK1.8最重要的就是引入了紅黑樹的設計(當衝突的鏈表長度超過8個的時候),為什麼要這樣設計呢?好處就是避免在最極端的情況下衝突鏈表變得很長很長,在查詢的時候,效率會非常慢。
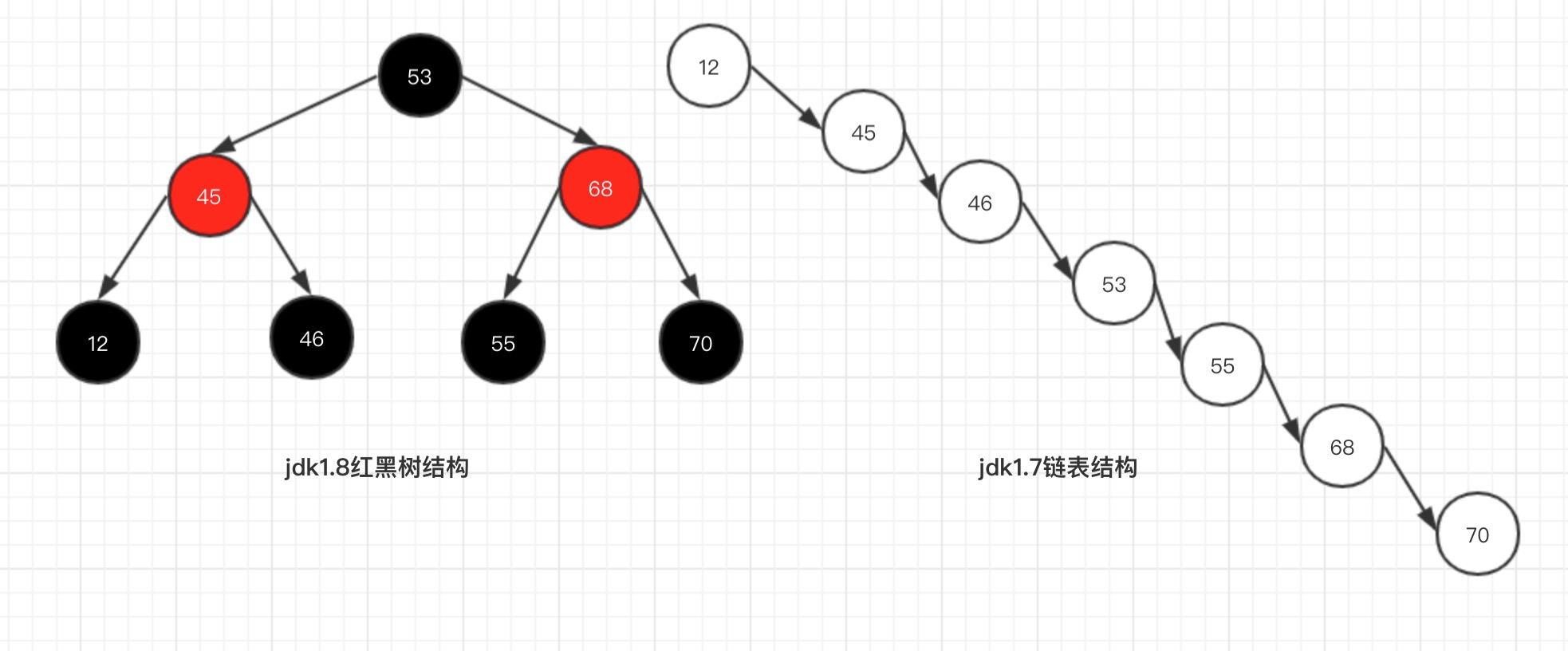
- 紅黑樹查詢:其訪問性能近似於折半查找,時間複雜度O(logn);
- 鏈表查詢:這種情況下,需要遍歷全部元素才行,時間複雜度O(n);
本文主要是講解紅黑樹的實現,只有充分理解了紅黑樹,對於後面的分析才會更加順利。
簡單的說,紅黑樹是一種近似平衡的二叉查找樹,其主要的優點就是“平衡“,即左右子樹高度幾乎一致,以此來防止樹退化為鏈表,通過這種方式來保障查找的時間複雜度為log(n)。
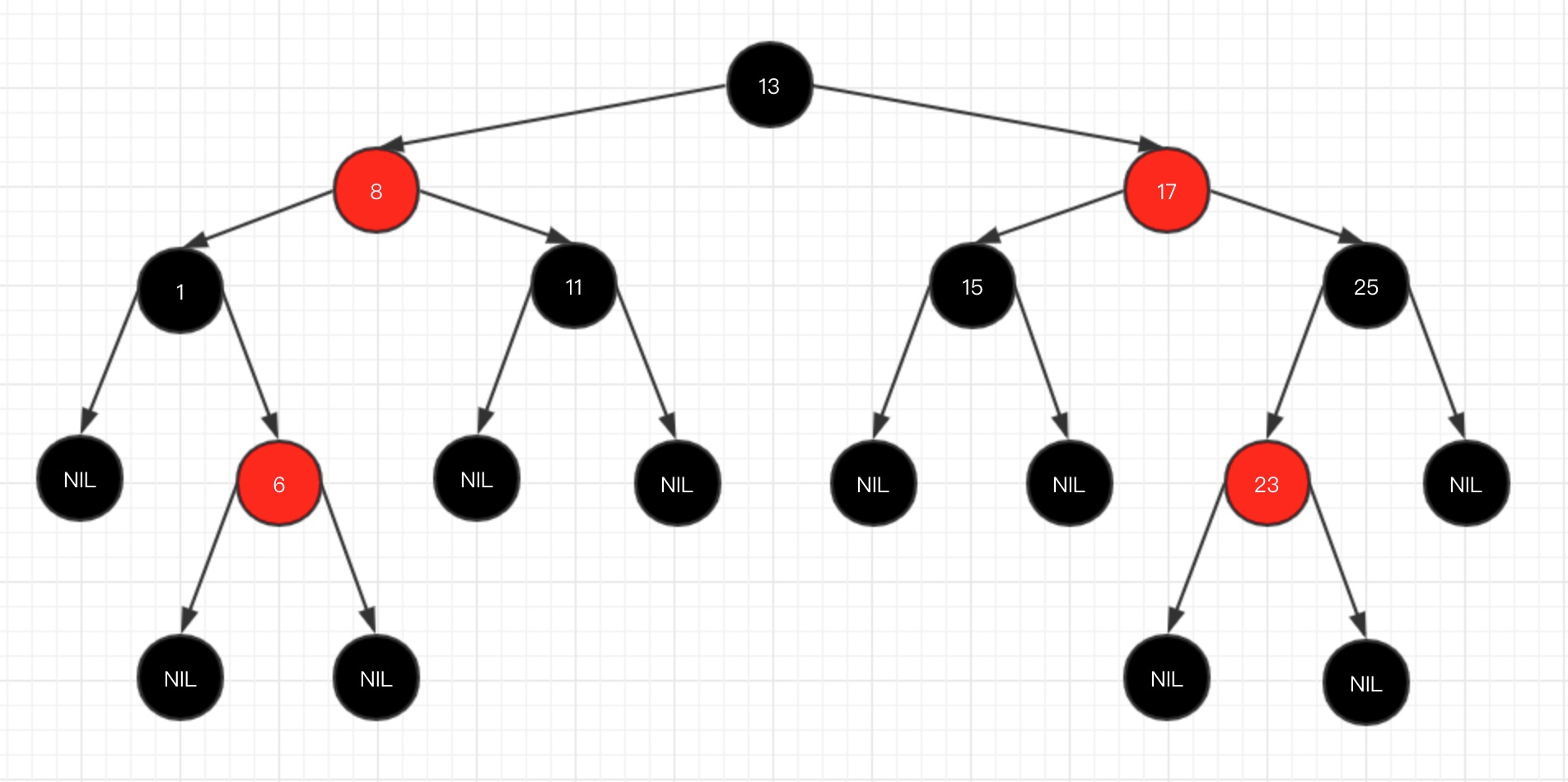
關於紅黑樹的內容,網上給出的內容非常多,主要有以下幾個特性:
- 1、每個節點要麼是紅色,要麼是黑色,但根節點永遠是黑色的;
- 2、每個紅色節點的兩個子節點一定都是黑色;
- 3、紅色節點不能連續(也即是,紅色節點的孩子和父親都不能是紅色);
- 4、從任一節點到其子樹中每個葉子節點的路徑都包含相同數量的黑色節點;
- 5、所有的葉節點都是是黑色的(註意這裡說葉子節點其實是上圖中的 NIL 節點);
在樹的結構發生改變時(插入或者刪除操作),往往會破壞上述條件3或條件4,需要通過調整使得查找樹重新滿足紅黑樹的條件。
二、調整方式
上面已經說到當樹的結構發生改變時,紅黑樹的條件可能被破壞,需要通過調整使得查找樹重新滿足紅黑樹的條件。
調整可以分為兩類:一類是顏色調整,即改變某個節點的顏色,這種比較簡單,直接將節點顏色進行轉換即可;另一類是結構調整,改變檢索樹的結構關係。結構調整主要包含兩個基本操作:左旋(Rotate Left),右旋(RotateRight)。
2.1、左旋
左旋的過程是將p的右子樹繞p逆時針旋轉,使得p的右子樹成為p的父親,同時修改相關節點的引用,使左子樹的深度加1,右子樹的深度減1,通過這種做法來調整樹的穩定性。過程如下:
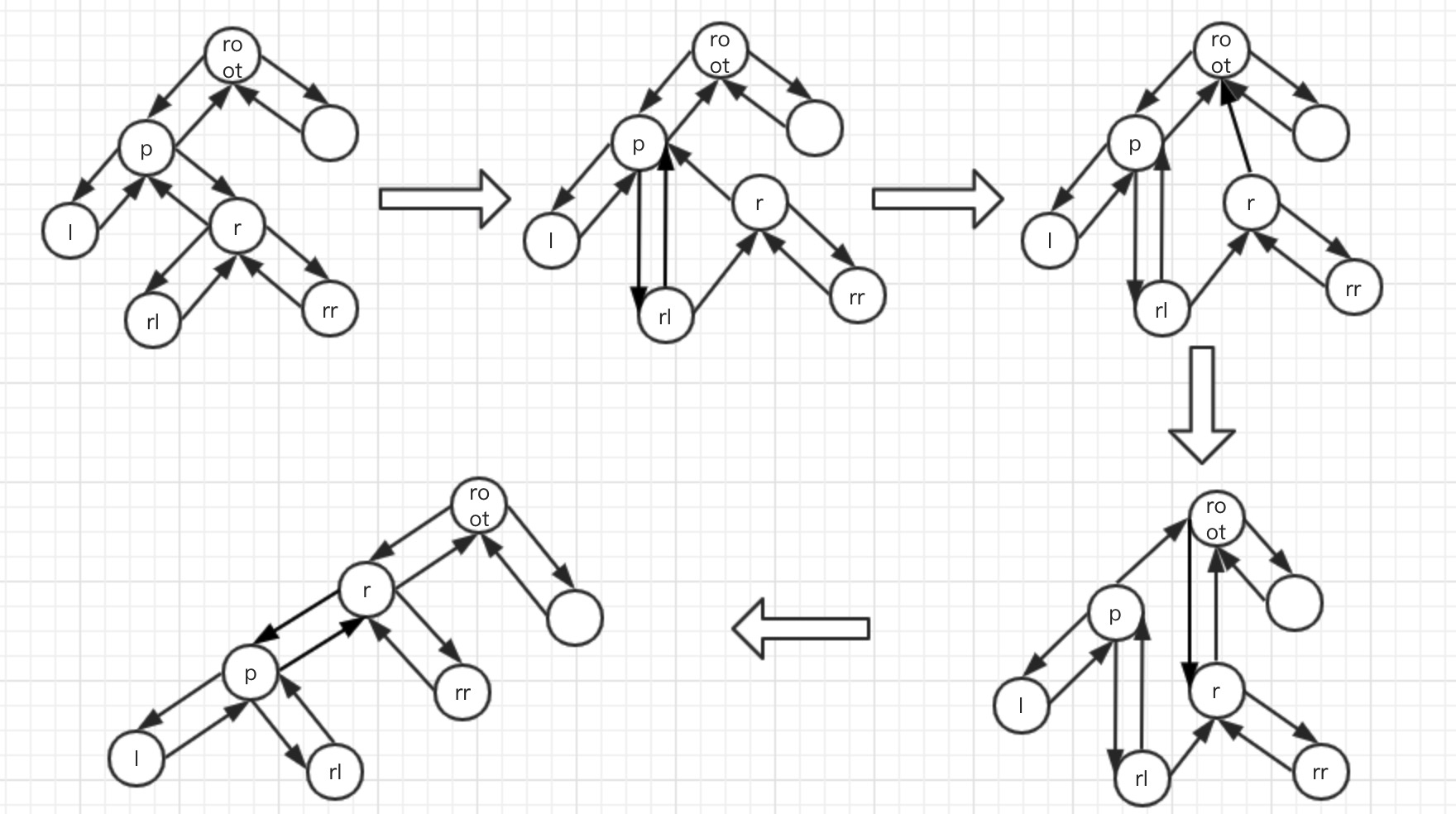
以jdk1.8為例,打開HashMap的源碼部分,紅黑樹內部類TreeNode屬性分析:
static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
//指向父節點的指針
TreeNode<K,V> parent;
//指向左孩子的指針
TreeNode<K,V> left;
//指向右孩子的指針
TreeNode<K,V> right;
//前驅指針,跟next屬性相反的指向
TreeNode<K,V> prev;
//是否為紅色節點
boolean red;
......
}左旋方法rotateLeft如下:
/*
* 左旋邏輯
*/
static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,
TreeNode<K,V> p) {
//root:表示根節點
//p:表示要調整的節點
//r:表示p的右節點
//pp:表示p的parent節點
//rl:表示p的右孩子的左孩子節點
TreeNode<K,V> r, pp, rl;
//r判斷,如果r為空則旋轉沒有意義
if (p != null && (r = p.right) != null) {
//多個等號的連接操作從右往左看,設置rl的父親為p
if ((rl = p.right = r.left) != null)
rl.parent = p;
//判斷p的父親,為空,為根節點,根節點的話就設置為黑色
if ((pp = r.parent = p.parent) == null)
(root = r).red = false;
//判斷p節點是左兒子還是右兒子
else if (pp.left == p)
pp.left = r;
else
pp.right = r;
r.left = p;
p.parent = r;
}
return root;
}2.2、右旋
瞭解了左旋轉之後,相應的就會有右旋,邏輯基本也是一樣,只是方向變了。右旋的過程是將p的左子樹繞p順時針旋轉,使得p的左子樹成為p的父親,同時修改相關節點的引用,使右子樹的深度加1,左子樹的深度減1,通過這種做法來調整樹的穩定性。實現過程如下:

同樣的,右旋方法rotateRight如下:
/*
* 右旋邏輯
*/
static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root,
TreeNode<K,V> p) {
//root:表示根節點
//p:表示要調整的節點
//l:表示p的左節點
//pp:表示p的parent節點
//lr:表示p的左孩子的右孩子節點
TreeNode<K,V> l, pp, lr;
//l判斷,如果l為空則旋轉沒有意義
if (p != null && (l = p.left) != null) {
//多個等號的連接操作從右往左看,設置lr的父親為p
if ((lr = p.left = l.right) != null)
lr.parent = p;
//判斷p的父親,為空,為根節點,根節點的話就設置為黑色
if ((pp = l.parent = p.parent) == null)
(root = l).red = false;
//判斷p節點是右兒子還是左兒子
else if (pp.right == p)
pp.right = l;
else
pp.left = l;
l.right = p;
p.parent = l;
}
return root;
}三、操作示例介紹
3.1、插入調整過程圖解

3.2、刪除調整過程圖解
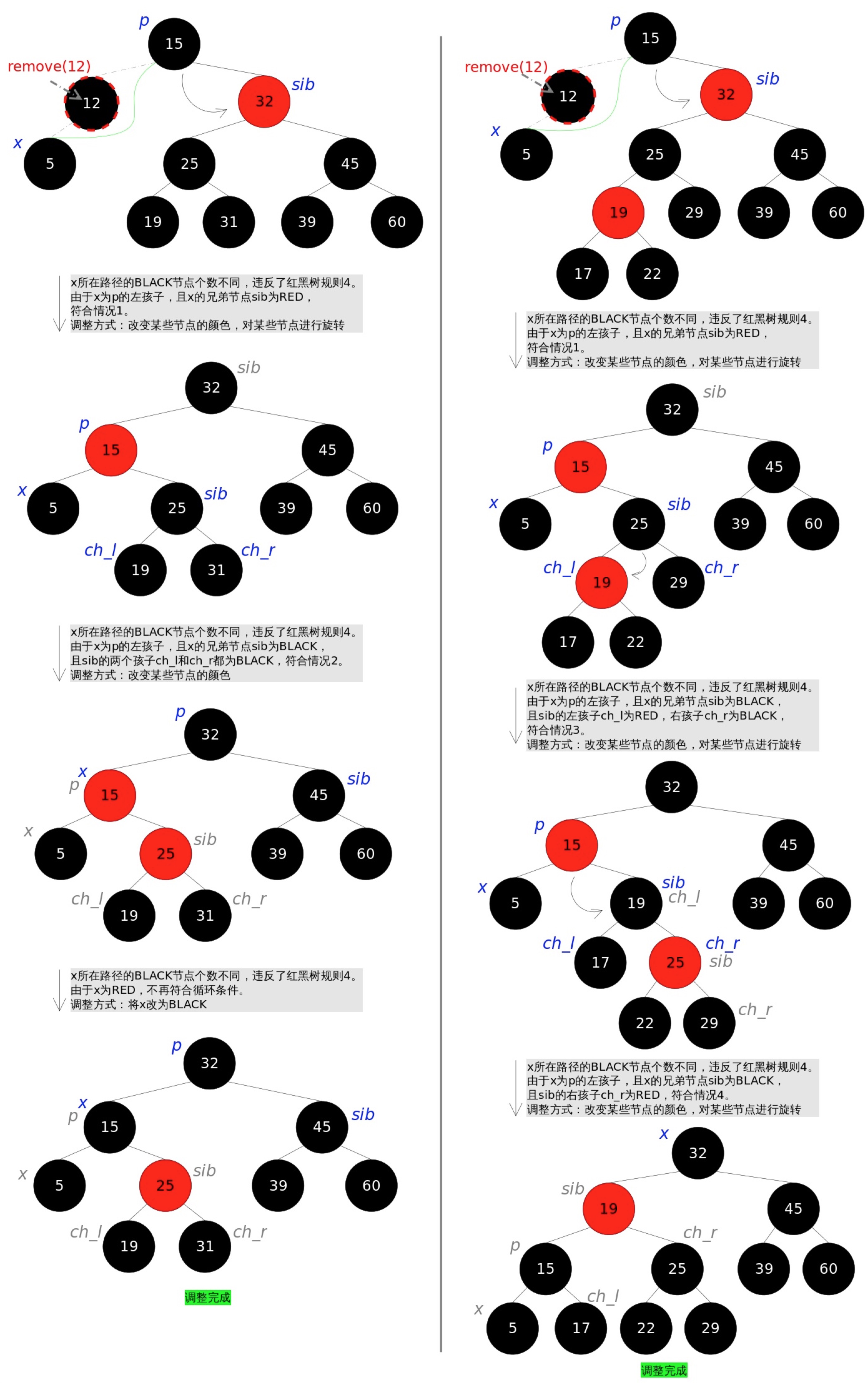
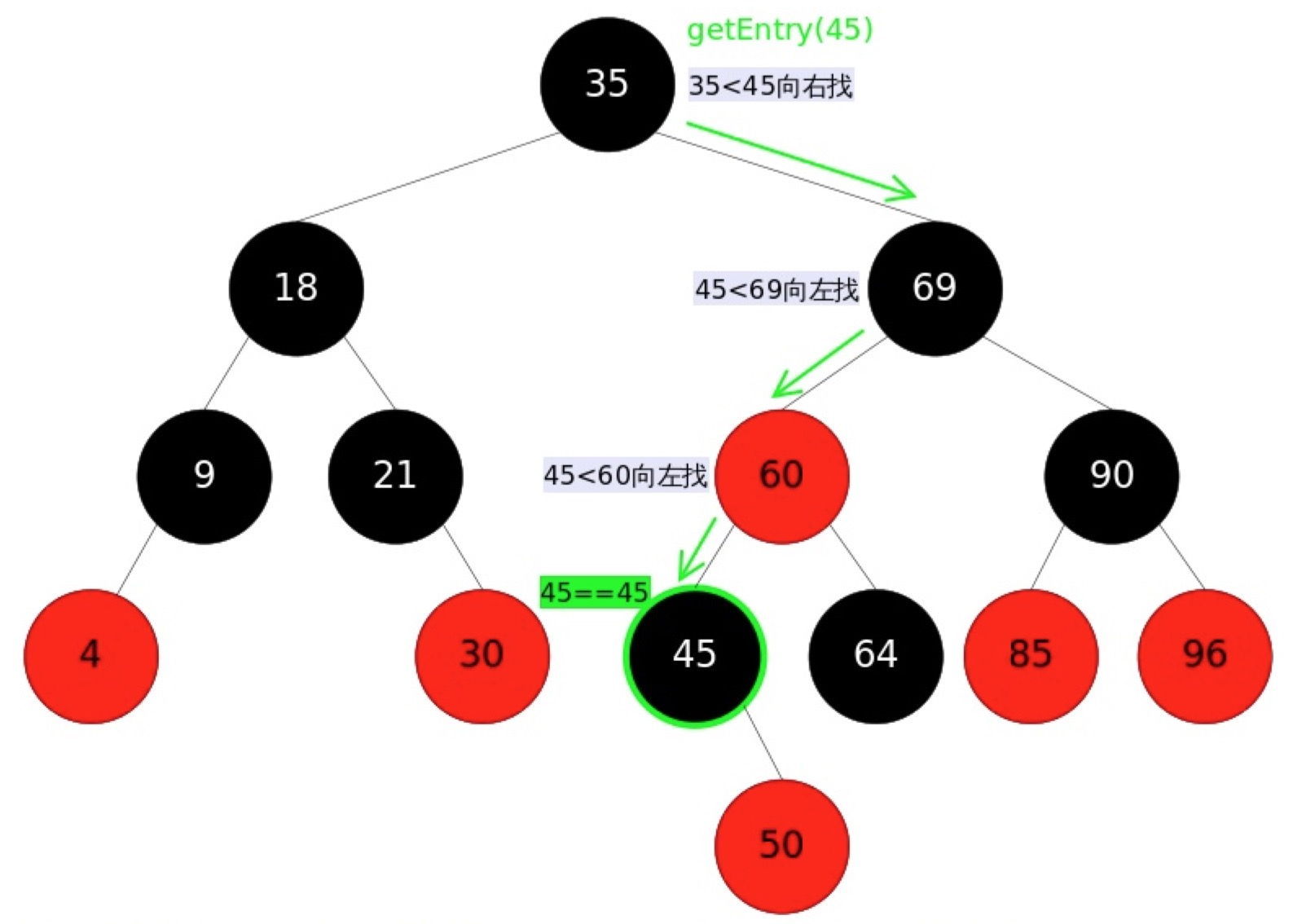
3.3、查詢過程圖解
四、總結
至此,紅黑樹的實現就基本完成了,關於紅黑樹的結構,有很多種情況,情況也比較複雜,但是整體調整流程,基本都是先調整結構然後調整顏色,直到最後滿足紅黑樹特性要求為止。整篇文章,如果有理解不當之處,歡迎指正!
五、參考
1、簡書 - JDK1.8紅黑樹實現分析
2、知乎 - 史上最清晰的紅黑樹講解
作者:炸雞可樂
出處:www.pzblog.cn



