二叉查找樹是將一組無序的數據構建成一顆有序數據的樹,其設計思想與二分法類似。很好的提高了海量數據查找效率,使得由從頭遍歷到尾的方式轉為二分查找的方式,時間複雜度從O(n)降低為O(log(n))。 ...
二叉查找樹是將一組無序的數據構建成一顆有序數據的樹,其設計思想與二分法類似。很好的提高了海量數據查找效率,使得由從頭遍歷到尾的方式轉為二分查找的方式,時間複雜度從O(n)降低為O(log(n))。
概念
- 結點:樹上的每個元素。
- 根結點:沒有父結點的結點。
- 父結點:結點的上一級結點。
- 子結點:結點的下一級結點。
- 葉子結點:沒有子結點的結點。
- 兄弟結點:擁有同一父結點的相鄰結點。
- 結點的度:一個結點中擁有子結點的個數。
- 樹的度:樹上最大結點的度。
- 結點的層次:以根結點為1,每深入一個子結點層次加1。
- 樹的高度:樹中最大的結點的層次。
特性
- 左子樹所有的結點值均小於,等於根結點值或為空。
- 左子樹所有的結點值均大於,等於根結點值或為空。
- 左、右子樹也分別為二叉排序樹。
- 沒有鍵值相等的結點。
構建
構建二叉查找樹,主要把握幾條原則,小於當前結點的在左邊,大於的在右邊,相等的不予處理。但是情況下結合實際業務需求,也可在相等時放在左結點或右結點,但是必須統一規則,不能左右都存在相等的。
創建結點對象:
package com.ytao.bst;
/**
* Created by YANGTAO on 2019/11/3 0003.
*/
public class Node {
private Integer value;
private Node leftChildren;
private Node rightChildren;
public Integer getValue() {
return value;
}
public void setValue(Integer value) {
this.value = value;
}
public Node getLeftChildren() {
return leftChildren;
}
public void setLeftChildren(Node leftChildren) {
this.leftChildren = leftChildren;
}
public Node getRightChildren() {
return rightChildren;
}
public void setRightChildren(Node rightChildren) {
this.rightChildren = rightChildren;
}
public Node(Integer value) {
this.value = value;
}
}
創建樹的實現:
package com.ytao.bst;
/**
* Created by YANGTAO on 2019/11/3 0003.
*/
public class BuildBST {
private Node rootNode = null;
public Node build(int[] vals){
// 遍歷所有數據,每次都需從根結點開始尋找左或右子節點為空的位置添加
for (int val : vals) {
this.assemble(rootNode, val);
}
return rootNode;
}
private void assemble(Node node, int val){
// 創建根結點
if (node == null){
rootNode = new Node(val);
}else{
// 根據左小右大特性判斷
if (val < node.getValue()){
Node leftNode = node.getLeftChildren();
// 如果左子結點為空,就添加為當前結點的左結點,否則繼續遞歸下去
if (leftNode == null){
node.setLeftChildren(new Node(val));
}else{
this.assemble(node.getLeftChildren(), val);
}
}else{
Node rightNode = node.getRightChildren();
// 如果右子結點為空,就添加為當前結點的右結點,否則繼續遞歸下去
if (rightNode == null){
node.setRightChildren(new Node(val));
}else{
this.assemble(rightNode, val);
}
}
}
}
}使用[7,5,9,2,11,6]測試是否滿足我們創建樹的要求:
public static void main(String[] args) {
int[] vals = {7,5,9,2,11,6};
Node node = new BuildBST().build(vals);
System.out.println(new Gson().toJson(node));
}測試結果滿足我們要求
{
"value": 7,
"leftChildren": {
"value": 5,
"leftChildren": {
"value": 2
},
"rightChildren": {
"value": 6
}
},
"rightChildren": {
"value": 9,
"rightChildren": {
"value": 11
}
}
}查找
假設從一百萬個數字中獲取值為88的數據,如果我們使用遍歷的方式,最糟的情況就是排在第一百萬個位置的時候,需要我們遍歷一百萬次才能獲取到數據,這就是我們最不想遇到的情況。這時將一百萬個數據構建成二叉查找樹,我們就可通過樹快速找到我們想要的數據。
由於設定一百萬個數據比較多,這裡我們舉例當前擁有數據[7,5,9,2,11,6],我們要找出其中的6。
使用迴圈遍歷所有數據的方法,我們需要6次遍歷 7->5->9->2->11->6。
使用二叉查找樹查找時,首先構建好的二叉查找樹的結構如圖:
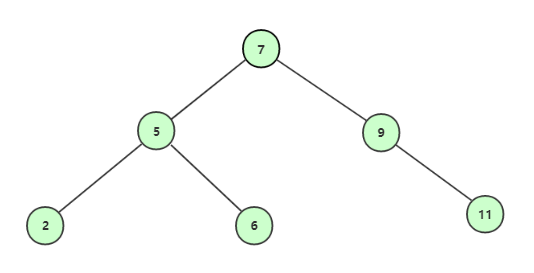
從根結點開始查找;
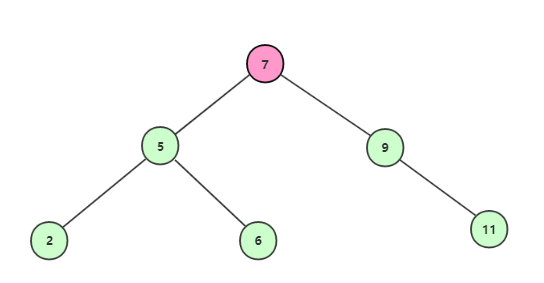
獲取根結點7,不等於6,且6<7,所以繼續找左子結點;
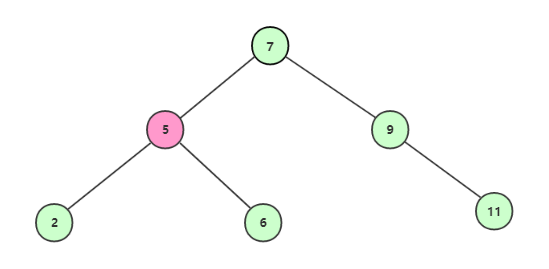
獲取到結點5,不等於6,且6>5,所以繼續找右子節點;
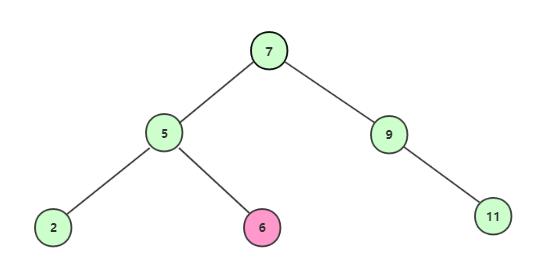
最終獲取到結點6,滿足我們需要的條件。所遍歷的數據為 7->5->6。
代碼實現查找:
package com.ytao.bst;
/**
* Created by YANGTAO on 2019/11/3 0003.
*/
public class SearchBST {
public Node search(Node node, int val){
// 如果結點為空,說明是沒有了符合的結點
if (node == null)
return null;
int nodeVal = node.getValue();
// 如果結點上的鍵值相等,就是我們需要找的結點
if (val == nodeVal){
return node;
}else if (val < nodeVal){ // 如果小於結點的值,那麼一定在結點的左子樹中
return this.search(node.getLeftChildren(), val);
}else{
return this.search(node.getRightChildren(), val);
}
}
}
插入
二叉查找樹的插入規則,必須是要插入後的結點是作為葉子結點。現在向上面的樹中插入10,根據上面所分析到的規則,為確保二叉查找樹的完整性,最終的插入流程為7->9->11->10:
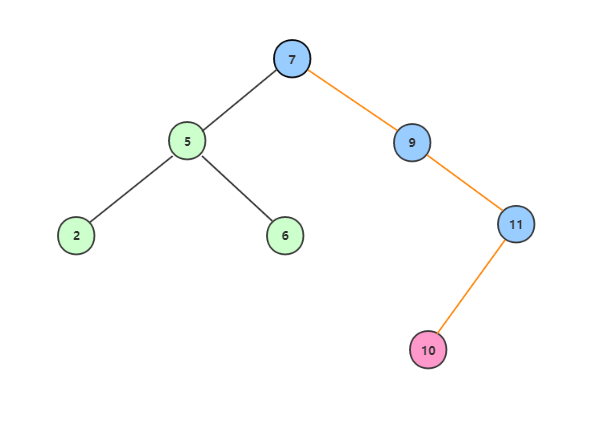
代碼實現:
package com.ytao.bst;
/**
* Created by YANGTAO on 2019/11/3 0003.
*/
public class InsertBST {
public void inesrt(Node node, int newVal){
// 當結點為空是,說明是作為根結點
if (node == null){
node = new Node(newVal);
}
int nodeVal = node.getValue();
// 如果小於結點的值,插入到左子樹中,大於就插入右子樹中
if (newVal < nodeVal){
Node leftNode = node.getLeftChildren();
// 為空時,說明為葉子結點,可插入
if (leftNode == null){
node.setLeftChildren(new Node(newVal));
}else {
this.inesrt(leftNode, newVal);
}
}else if (newVal > nodeVal){
Node rightNode = node.getRightChildren();
if (rightNode == null){
node.setRightChildren(new Node(newVal));
}else {
this.inesrt(rightNode, newVal);
}
}else {
// todo 相等時,可根據具體業務處理,放棄,或在左右樹中選擇一個
}
}
}
刪除
刪除結點分為多種情況,其中主要分析的:
葉子結點
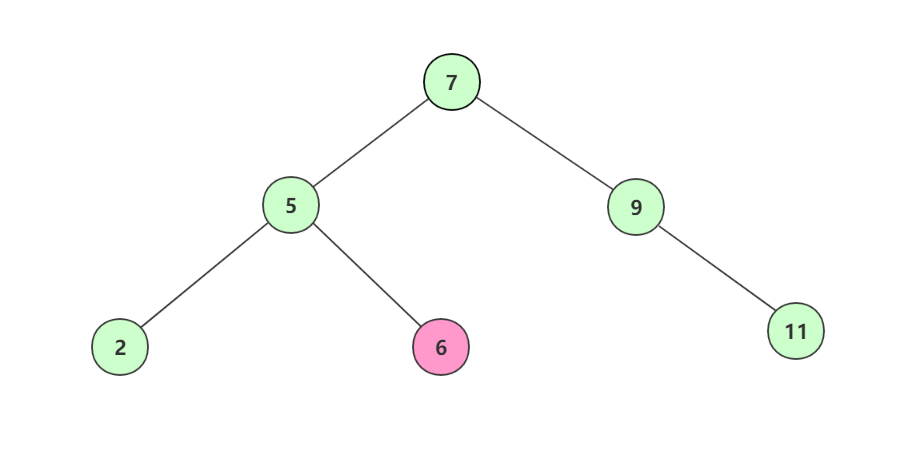
刪除葉子結點,將所要刪除的葉子結點直接刪除便可,比如刪除結點6。
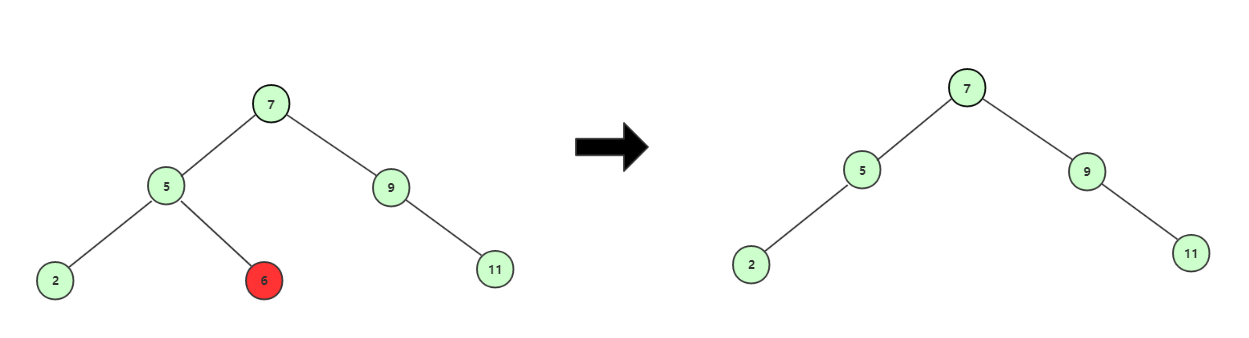
單子結點的結點
被刪除結點,如果只有一個子結點,那麼被刪除結點刪除後,該結點的子結點補上其位置,比如刪除結點9。
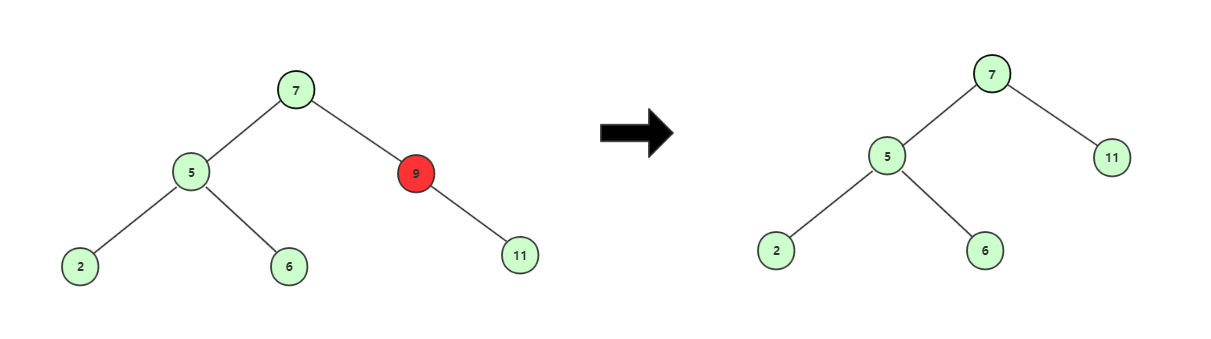
存在左右子結點的結點
為了更加清楚表達刪除存在左右結點的結點,先向樹中多添加3個結點8,10,15。然後刪除結點9。
這裡的解決方法就是,刪除9後,可以用前驅結點或後繼結點補上。前驅結點為左子樹中最大的結點,後繼結點為右子樹中最小的結點。
現在以後繼結點補上的方案為:
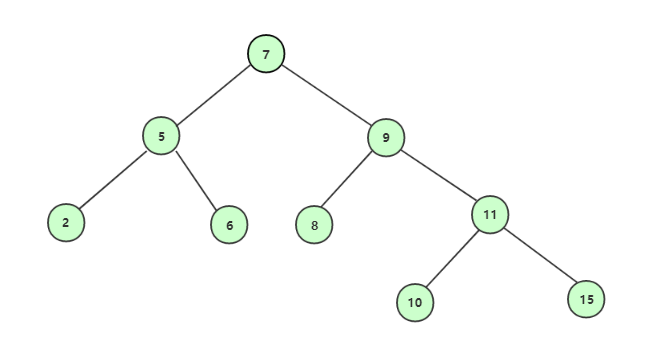
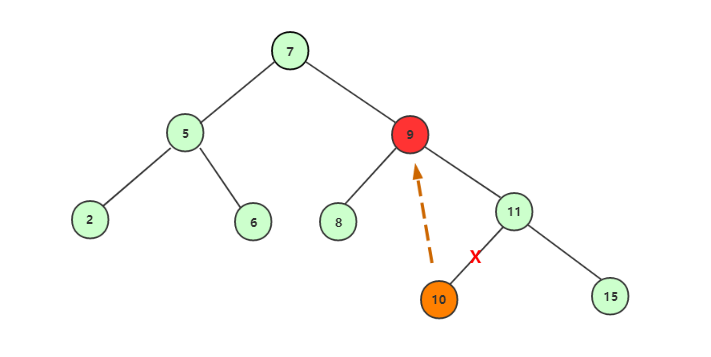
後繼結點補上刪除後的結點:
完成刪除,後繼結點補充上後:
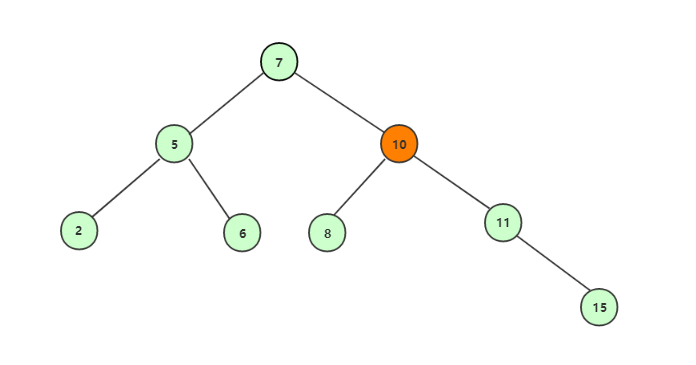
代碼實現:
package com.ytao.bst;
/**
* Created by YANGTAO on 2019/11/3 0003.
*/
public class DeleteBST {
public Node delete(Node node, int delVal) {
// 為空時,代表葉子結點
if (node == null){
return node;
}
int nodeVal = node.getValue();
Node leftNode = node.getLeftChildren();
Node rightNode = node.getRightChildren();
// 刪除的結點,與遍歷到的當前結點做比較,小於,大於或等於
if (delVal < nodeVal){
Node tempLeftNode = delete(leftNode, delVal);
node.setLeftChildren(tempLeftNode);
} else if(delVal > nodeVal){
Node tempRightNode = delete(rightNode, delVal);
node.setRightChildren(tempRightNode);
} else {
// 刪除的結點與當前遍歷到的結點相等時
// 並且左結點為空時,返回右結點去補上刪除的位置,反則返回左結點補上
// 說明刪除結點為單子結點的情況
if (leftNode == null){
return rightNode;
} else if (rightNode == null){
return leftNode;
}
// 通過查詢最小右結點,獲取後繼結點
Node minNode = minNode(rightNode);
int minNodeValue = minNode.getValue();
node.setValue(minNodeValue);
// 刪除後繼結點
Node tempRightNode = delete(rightNode, minNodeValue);
node.setRightChildren(tempRightNode);
}
return node;
}
private Node minNode(Node node) {
// 一直尋找最小值,知道左子節點為空為止
Node leftNode = node.getLeftChildren();
if (leftNode != null)
return minNode(leftNode);
return node;
}
}
至此上面三中情況都予滿足。
總結
上面對二叉查找樹的操作都已介紹,但是正真使用中,是要結合實際業務進行相關調整來滿足自己的需求,不然,一切的優化手段都是假把式。二叉查找樹雖然好用,但是它也是有一定要求,在數據量不大的情況下,使用遍歷的方式,更加符合我們的要求,所以它使用場景一般是在海量數據的查詢,用來提查詢效率。
個人博客: https://ytao.top
我的公眾號 ytao




