眾所周知,線段樹是algo中很重要的一項! 一.簡介 線段樹是一種二叉搜索樹,與區間樹相似,它將一個區間劃分成一些單元區間,每個單元區間對應線段樹中的一個葉結點。 使用線段樹可以快速的查找某一個節點在若幹條線段中出現的次數,時間複雜度為O(logN)。而未優化的空間複雜度為2N,實際應用時一般還要開 ...
眾所周知,線段樹是algo中很重要的一項!
一.簡介
線段樹是一種二叉搜索樹,與區間樹相似,它將一個區間劃分成一些單元區間,每個單元區間對應線段樹中的一個葉結點。
使用線段樹可以快速的查找某一個節點在若幹條線段中出現的次數,時間複雜度為O(logN)。而未優化的空間複雜度為2N,實際應用時一般還要開4N的數組以免越界,因此有時需要離散化讓空間壓縮。
二.用途
單點 : 查詢(query)修改(add,mul)
區間 : 查詢(區間和),修改,最大值(max),最小值(min)。
三. 實現方式
1.建樹
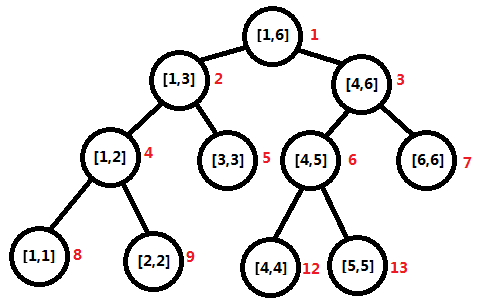
由於每個點都表示一個區間,所以他有很多信息(左兒子,右兒子,區間sum) 所以我們用結構體存. 因為之後要用到懶標記,所以結構體還有兩個懶標記。
懶標記 : 以上圖為例,如果想在1 - 6區間內加一,我們就將這個信息從根節點傳遞到下一層,這時2,3點都有一個add = 1的懶標記,這樣就表示已經加過1了,下次如果還要加,那麼直接加在懶標記上。就比如你掙了一筆錢,暫時不用,就存在銀行里了。之後如果求解需要遞歸,那麼這個懶標記就向下傳,並且傳完後自己要清零!(這樣更新後的狀態就是 原狀態 + 子區間點的個數 * 傳下里的懶標記,(example sum = 5(原狀態)+ 4(區間里有4個數,都加了個2) * 2(懶標記))-------很玄學
乘法的懶標記(luogu p3373):需要特別註意下
比如 懶標記原本為2 + 3
現在傳下一個乘8 那麼就變為(2 + 3) * 8
然後再傳一個加三,就會變成(2 + 3 + 3) * 8
所以我們這麼存 2 * 8 + 3 * 8
這樣加3後值才是正確的!
上代碼
代碼中% P 為題目要求
1 struct Node { 2 int l, r; 3 ll sum; 4 ll add, mul; 5 6 Node() { 7 l = r = sum = add = 0; 8 mul = 1; 9 } 10 11 void update_add(ll value) { 12 add = (add + value) % P; 13 sum = (sum + (r - l + 1) * value) % P; 14 } 15 16 void update_mul(ll value) { 17 sum = (sum * value) % P; 18 mul = (mul * value) % P; 19 add = (add * value) % P; 20 } 21 } t[N << 2];
我的建樹可能比較怪,當遞歸到根節點再cin,一邊遞歸一邊更新(push_up,後面有)
1 void build_tree(int p, int l, int r) { 2 t[p].l = l, t[p].r = r; 3 if (l == r) { 4 cin >> t[p].sum; 5 return; 6 } 7 int mid = (t[p].l + t[p].r) >> 1; 8 build_tree(lc(p), l, mid); 9 build_tree(rc(p), mid + 1, r); 10 push_up(p); 11 }
左兒子右兒子
inline int lc(int p) { return p << 1; } inline int rc(int p) { return p << 1 | 1; }
向上push_up更新信息(sum),向下傳懶標記(push_down) 切記傳完後自己狀態要恢復哦!
1 void push_up(int p) { 2 t[p].sum = t[lc(p)].sum + t[rc(p)].sum; 3 } 4 5 void push_down(int p) { 6 if (t[p].mul != 1) { 7 t[lc(p)].update_mul(t[p].mul); 8 t[rc(p)].update_mul(t[p].mul); 9 t[p].mul = 1; 10 } 11 if (t[p].add) { 12 t[lc(p)].update_add(t[p].add); 13 t[rc(p)].update_add(t[p].add); 14 t[p].add = 0; 15 } 16 }
Å%%%Then
當我們進行區間改動時
(黑色為總區間,紅色為需要修改的區間)
如果當前區間是全部區間的子集————那很好,咱們可以直接修改

如果當前區間和總區間有交集,那麼就遞歸,找到第一個完全包含他的區間,然後修改,再遞歸上去
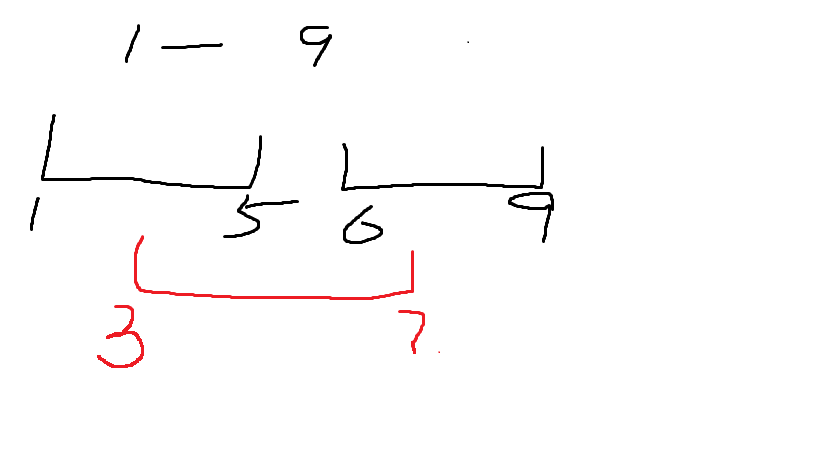
上代碼!!!
1 void update1(int p, int l, int r, ll value) {//乘法更新 2 if (t[p].l >= l && t[p].r <= r) { 3 t[p].update_mul(value); 4 return; 5 } 6 push_down(p); 7 int mid = (t[p].l + t[p].r) >> 1; 8 if (l <= mid) update1(lc(p), l, r, value); 9 if (r > mid) update1(rc(p), l, r, value); 10 push_up(p); 11 } 12 13 void update2(int p, int l, int r, ll value) {//加法更新 14 if (t[p].l >= l && t[p].r <= r) { 15 t[p].update_add(value); 16 return; 17 } 18 push_down(p); 19 int mid = (t[p].l + t[p].r) >> 1; 20 if (l <= mid) update2(lc(p), l, r, value); 21 if (r > mid) update2(rc(p), l, r, value); 22 push_up(p); 23 } 24 25 ll query(int p, int l, int r) {//區間查詢,如果是單點差距的話l == r 26 if (t[p].l >= l && t[p].r <= r) { 27 return t[p].sum % P; 28 } 29 push_down(p); 30 ll sum = 0; 31 int mid = (t[p].l + t[p].r) >> 1; 32 if (l <= mid) sum = (sum + query(lc(p), l, r)) % P; 33 if (r > mid) sum = (sum + query(rc(p), l, r)) % P; 34 return sum % P; 35 }
當然還可以求RMQ問題
1 struct Node 2 { 3 ll minn,maxx; 4 }t[]; 5 6 //build 裡加幾句 7 t[p].maxx = max(t[lc(p)].maxx,t[rp(p)].maxx); 8 t[p].minn = min(t[lc(p)].minn,t[rp(p)].minn); 9 10 11 int ans1,ans2; 12 void new_query(int p,int l,int r) 13 { 14 if(t[p].l == l && t[p].r == r) 15 { 16 ans1 = max(ans1,t[p].maxx); 17 ans2 = max(ans2,t[p].minn); 18 return; 19 } 20 int mid = (t[p].l + t[p].r) >> 1; 21 if(r <= mid) 22 query(lc(p),l,r); 23 else if (l > mid) 24 query(rc(p),l,r); 25 else 26 { 27 query(lc(p),l,mid); 28 query(rp(p),mid + 1,r); 29 } 30 }
下麵附上總代碼(代碼按照luogu 線段樹2的模板打的,可AC)

1 #include <iostream> 2 #include<algorithm> 3 using namespace std; 4 const int N = 1e5 + 7; 5 typedef long long ll; 6 7 ll P; 8 9 struct Node { 10 int l, r; 11 ll sum; 12 ll add, mul; 13 // ll minn,mmax; 14 Node() { 15 l = r = sum = add = 0; 16 mul = 1; 17 } 18 19 void update_add(ll value) { 20 add = (add + value) % P; 21 sum = (sum + (r - l + 1) * value) % P; 22 } 23 24 void update_mul(ll value) { 25 sum = (sum * value) % P; 26 mul = (mul * value) % P; 27 add = (add * value) % P; 28 } 29 } t[N << 2]; 30 31 inline int lc(int p) { 32 return p << 1; 33 } 34 35 inline int rc(int p) { 36 return p << 1 | 1; 37 } 38 39 void push_up(int p) { 40 t[p].sum = t[lc(p)].sum + t[rc(p)].sum; 41 } 42 43 void push_down(int p) { 44 if (t[p].mul != 1) { 45 t[lc(p)].update_mul(t[p].mul); 46 t[rc(p)].update_mul(t[p].mul); 47 t[p].mul = 1; 48 } 49 if (t[p].add) { 50 t[lc(p)].update_add(t[p].add); 51 t[rc(p)].update_add(t[p].add); 52 t[p].add = 0; 53 } 54 } 55 56 void build_tree(int p, int l, int r) { 57 t[p].l = l, t[p].r = r; 58 if (l == r) { 59 cin >> t[p].sum; 60 return; 61 } 62 int mid = (t[p].l + t[p].r) >> 1; 63 build_tree(lc(p), l, mid); 64 build_tree(rc(p), mid + 1, r); 65 // t[p].maxx = max(t[lc(p)].maxx,t[rp(p)].maxx); 66 // t[p].minn = min(t[lc(p)].minn,t[rp(p)].minn); 67 push_up(p); 68 } 69 70 void update1(int p, int l, int r, ll value) { 71 if (t[p].l >= l && t[p].r <= r) { 72 t[p].update_mul(value); 73 return; 74 } 75 push_down(p); 76 int mid = (t[p].l + t[p].r) >> 1; 77 if (l <= mid) update1(lc(p), l, r, value); 78 if (r > mid) update1(rc(p), l, r, value); 79 push_up(p); 80 } 81 82 void update2(int p, int l, int r, ll value) { 83 if (t[p].l >= l && t[p].r <= r) { 84 t[p].update_add(value); 85 return; 86 } 87 push_down(p); 88 int mid = (t[p].l + t[p].r) >> 1; 89 if (l <= mid) update2(lc(p), l, r, value); 90 if (r > mid) update2(rc(p), l, r, value); 91 push_up(p); 92 } 93 94 ll query(int p, int l, int r) { 95 if (t[p].l >= l && t[p].r <= r) { 96 return t[p].sum % P; 97 } 98 push_down(p); 99 ll sum = 0; 100 int mid = (t[p].l + t[p].r) >> 1; 101 if (l <= mid) sum = (sum + query(lc(p), l, r)) % P; 102 if (r > mid) sum = (sum + query(rc(p), l, r)) % P; 103 return sum % P; 104 } 105 /*int ans1,ans2; 106 void new_query(int p,int l,int r) 107 { 108 if(t[p].l == l && t[p].r == r) 109 { 110 ans1 = max(ans1,t[p].maxx); 111 ans2 = max(ans2,t[p].minn); 112 return; 113 } 114 int mid = (t[p].l + t[p].r) >> 1; 115 if(r <= mid) 116 new_query(lc(p),l,r); 117 else if (l > mid) 118 new_query(rc(p),l,r); 119 else 120 { 121 new_query(lc(p),l,mid); 122 new_query(rp(p),mid + 1,r); 123 } 124 } 125 */ 126 127 int main() 128 { 129 int n, m; 130 cin >> n >> m >> P; 131 build_tree(1, 1, n); 132 while (m--) { 133 int op, l, r, num; 134 cin >> op >> l >> r; 135 if (op == 1 || op == 2) cin >> num; 136 if (op == 1) update1(1, l, r, num); 137 else if (op == 2) update2(1, l, r, num); 138 else cout << query(1, l, r) << endl; 139 } 140 } 141 142 //Juddav007 0.0View Code(all)
THANKS FOR WATCHING!



