說明:《數學分析原理》指 г.м.菲赫金哥爾茨 著《數學分析原理》(第一卷 第九版)高等教育出版社 整數和分數統稱為有理數。有理數域不能完全滿足數學定義的需求,比如人們無法將一個邊長為1的正方形的對角線長度表示為有理數,也即 沒有一個其平方能等於2的有理數 ${\frac{{p}}{{q}}}$($ ...
說明:《數學分析原理》指 г.м.菲赫金哥爾茨 著《數學分析原理》(第一卷 第九版)高等教育出版社
整數和分數統稱為有理數。有理數域不能完全滿足數學定義的需求,比如人們無法將一個邊長為1的正方形的對角線長度表示為有理數,也即 沒有一個其平方能等於2的有理數 ${\frac{{p}}{{q}}}$(${p}$ 與 ${q}$ 是兩個自然數)存在(需要說明的是原書中的自然數相當於我們說的正整數)。下麵記錄書中用反證法證明這一結論的過程。
證明 1
論點:沒有一個其平方能等於2的有理數 ${\frac{{p}}{{q}}}$ (${p}$ 與 ${q}$ 是兩個自然數)存在
證法:反證法
證明:假定有這樣的分數 ${\frac{{p}}{{q}}}$ 存在,使得 ${{ \left( {\frac{{p}}{{q}}} \right) }\mathop{{}}\nolimits^{{2}}\text{ }=\text{ }2}$ 。可以假設這個分數是既約的,也就是說 ${p}$ 與 ${q}$ 無公因數,不可再約分。因 ${p\mathop{{}}\nolimits^{{2}}\text{ }=\text{ }2q\mathop{{}}\nolimits^{{2}}}$,所以 ${p}$ 是偶數。因 ${\frac{{p}}{{q}}}$ 既約,因而 ${q}$ 是奇數。設 ${p=2r}$(${r}$是整數),則有 ${p\mathop{{}}\nolimits^{{2}}\text{ }=\text{ }2q\mathop{{}}\nolimits^{{2}}\text{ }=\text{ }4r\mathop{{}}\nolimits^{{2}}}$,進而 ${q\mathop{{}}\nolimits^{{2}}\text{ }=\text{ }2r\mathop{{}}\nolimits^{{2}}}$ ,由此可推得 ${q}$ 是偶數,這與假設相矛盾,論點得證。
有理數域的不足在幾何中簡單地表現為 “不是所有的線段都能有長度”。例如,上述邊長為1的正方形其對角線長度的平方為2,但其對角線長度自身不能用有理數表示,這可由論點1得出。
書中擴充有理數域、定義無理數是通過記錄德國數學家戴德金關於討論有理數域內分割的概念得出的。考慮把全部有理數的集合分成兩個非空集合${A}$和${A'}$,即假定:
1. 每一個有理數在而且只在 ${A}$ 或 ${A'}$ 兩個集合中的一個
2. 集合${A}$中的每一個數 ${a}$小於集合 ${A'}$ 中的每一個數 ${a'}$
滿足這兩個條件的對有理數域的分法稱為“分割”。其中集合 ${A}$ 叫做分割的下類,集合A'叫做上類,分割可用 ${A|A'}$ 表示。書中證明,分割只能有以下三個類型:
1) 在下類 ${A}$ 中沒有最大的數,而在上類 ${A}$ 中有最小的數 ${a}$;
2) 在下類 ${A'}$ 中有最大的數 ${r}$,而在上類 ${A}$ 中沒有最小的數;
3) 既在下類中沒有最大的數,又在上類中沒有最小的數。
前兩種分割是由有理數 ${r}$ 產生的( ${r}$ 是 ${A}$ 與 ${A'}$ 兩類中間的界數),或者說,這分割定義了有理數 ${r}$。第三種情形下的界數在有理數域不存在,分割不能定義任何有理數,故而引進了無理數,且規定 任何屬於類型 3) 的分割定義了某一個無理數${α}$,${α}$就代替這缺少的界數。
下麵用圖示簡單表示這三種情形,並證明第三種情形。
分割一:
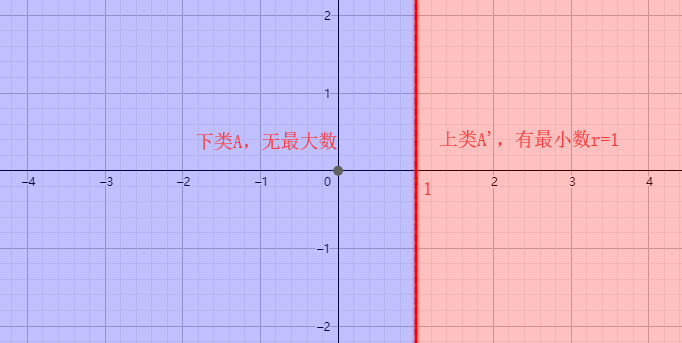
分割二:
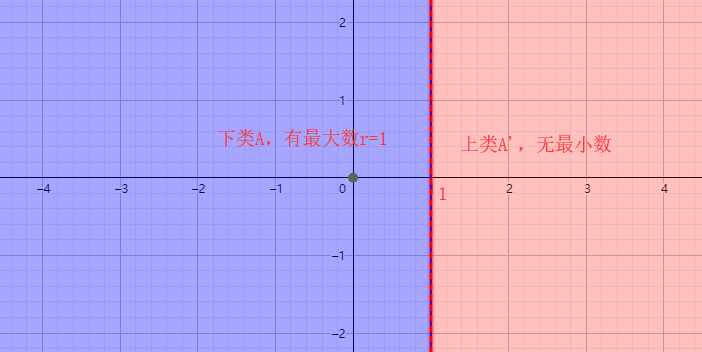
分割三:
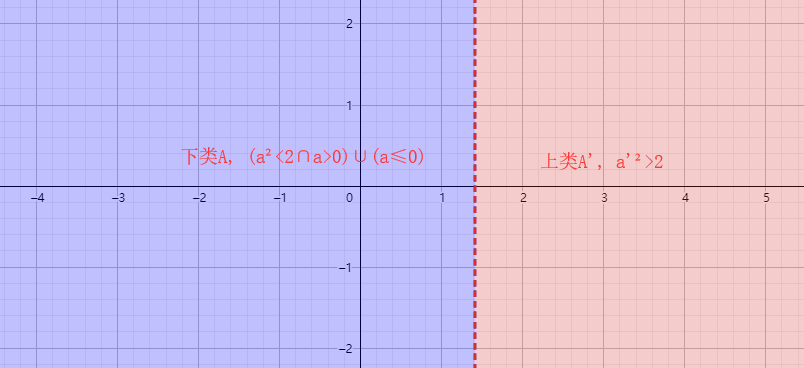
下麵先記錄書中對分割三第一種情形的證明,再仿照方法證明第二種情形。
證明 2
論點:在有理數域內,把一切使 ${a\mathop{{}}\nolimits^{{2}}\text{ } < \text{ }2}$ 的正有理數${a}$、${0}$及一切負有理數都歸入${A}$類,把一切使 ${\mathop{{a'}}\nolimits^{{2}}\text{ } > \text{ }2}$ 的正有理數${a'}$ 歸入${A'}$ 類,證明在 ${A}$ 類中既無最大數,在 ${A'}$ 類中也無最小數。
證法:放縮法不等式證明
證明:
(1). 首先,證明在 ${A}$ 類中無最大數
我們只需顯示證明 ${a\mathop{{}}\nolimits^{{2}}\text{ } < \text{ }2}$ 的情況,${a\mathop{{}}\nolimits^{{2}}\text{ } \le \text{ }0}$ 的情況很明顯成立。
設 ${a}$ 是 ${A}$ 類中的任一整數,則有${a\mathop{{}}\nolimits^{{2}} < 2}$,我們需證明如果可以有正數${n}$,使得
${{ \left( {a+\frac{{1}}{{n}}} \right) }\mathop{{}}\nolimits^{{2}}\text{ } < \text{ }2}$ (1),
也就是說讓 ${a+\frac{{1}}{{n}}}$ 也屬於${A}$類。展開不等式並移項可得
${\frac{{2a}}{{n}}+\frac{{1}}{{n\mathop{{}}\nolimits^{{2}}}}\text{ } < \text{ }2-a\mathop{{}}\nolimits^{{2}}}$ (2)
又對於正數${n}$,不妨取 ${n > 1}$,則有
${\frac{{1}}{{n\mathop{{}}\nolimits^{{2}}}}\text{ } < \text{ }}\frac{{1}}{{n}}$
不等式兩邊同時加正數 ${\frac{{2a}}{{n}}}$ 可得
${\frac{{2a}}{{n}}+\frac{{1}}{{n\mathop{{}}\nolimits^{{2}}}}\text{ } < \text{ }\frac{{2a}}{{n}}+\frac{{1}}{{n}}}$
亦即 ${\frac{{2a}}{{n}}+\frac{{1}}{{n\mathop{{}}\nolimits^{{2}}}}\text{ } < \text{ }\frac{{2a\text{ }+1}}{{n}}}$
如果 ${n}$ 滿足不等式 ${{\frac{{2a\text{ }+1}}{{n}}}\text{ } < \text{ }2-a\mathop{{}}\nolimits^{{2}}}$ ,則不等式成立 (2) 成立,進而不等式 (1) 成立。為此,只要取
${n\text{ } > \text{ }\frac{{2a+1}}{{2-a\mathop{{}}\nolimits^{{2}}}}}$
即可。由此可見,無論 ${a}$ 是 ${A}$ 類中怎樣的一個正數,在 ${A}$ 類中總能找到大於 ${a}$ 的數。聯繫 ${a\mathop{{}}\nolimits^{{2}}\text{ } \le \text{ }0}$ 的情況,在 ${A}$ 類中無最大數得證。
(2). 同理,證明在${A'}$類中無最小數
設 ${a'}$ 是 ${A'}$ 類中的任一整數,則有 ${\mathop{{a'}}\nolimits^{{2}}\text{ } > \text{ }2}$。我們需證明如果可以有正數 ${n}$ 使得
${{ \left( {a'-\frac{{1}}{{n}}} \right) }\mathop{{}}\nolimits^{{2}}\text{ } > \text{ }2}$ (3)
也就是說讓 ${a'-\frac{{1}}{{n}}}$ 也屬於 ${A'}$ 類。展開不等式 (3) 並移項可得:
${\frac{{1}}{{n\mathop{{}}\nolimits^{{2}}}}\text{ }-\text{ }\frac{{2a'}}{{n}}\text{ } > \text{ }2\text{ }-\text{ }a'\mathop{{}}\nolimits^{{2}}}$ (4)
對於正數 ${n}$,取 ${0 < n < 1}$,則有
${\frac{{1}}{{n\mathop{{}}\nolimits^{{2}}}}\text{ } > \text{ }\frac{{1}}{{n}}}$
不等式兩邊同時減去 ${\frac{{2a'}}{{n}}}$ 可得
${\frac{{1}}{{n\mathop{{}}\nolimits^{{2}}}}\text{ }-\text{ }\frac{{2a'}}{{n}}\text{ } > \text{ }\frac{{1}}{{n}}\text{ }-\text{ }\frac{{2a'}}{{n}}}$
亦即 ${\frac{{1}}{{n\mathop{{}}\nolimits^{{2}}}}\text{ }-\text{ }\frac{{2a'}}{{n}}\text{ } > \text{ }\frac{{1-2a'}}{{n}}}$
如果 ${n}$ 滿足不等式 ${\frac{{1-2a'}}{{n}}\text{ } > \text{ }2\text{ }-\text{ }a'\mathop{{}}\nolimits^{{2}}}$,則不等式 (4) 成立,進而不等式 (3) 成立。
為此,只要取
${n\text{ } < \text{ }\frac{{1-2a'}}{{a'\mathop{{}}\nolimits^{{2}}-2}}}$
即可。由此,無論${a'}$ 是 ${A'}$ 類中怎樣的一個正數,在 ${A'}$ 類中總能找到小於 ${a'}$ 的數。故,在 ${A'}$ 類中無最小數得證。
分割三在有理數域不存在界數,但可以在無理數域找到這個界數就是 ${{\sqrt{{2}}}}$。
事實上,在引進了無理數後,前述三種分割也可以統一起來。這建立在一下兩個規定之上:
(1). 有理數和無理數統稱為實數
(2). 將界數歸到上類
這樣,在實數域內定義的分割就是:
在下類 ${A}$ 中沒有最大的數,而在上類 ${A'}$ 中有最小的數 ${r}$ 。



