基礎為技術之本_重新認識斐波那契數列

斐波那契數列，是軟體人的一位老朋友了，今天我們就來回顧一下教科書上的寫法以及這種寫法性能上的弊端？有沒有更好的寫法？

1.首先，教科書的問法是求斐波那契數列的第N項；寫一個函數，輸入n,求出第N項目。數列定義如下：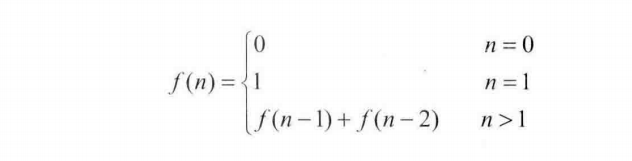

於是接下來就會引申出遞歸函數的用法，以及代碼（c#）實例：

 1 /// <summary>
 2 /// 斐波那契數列低級寫法
 3 /// </summary>
 4 /// <param name="targetNumber">輸入的目標值</param>
 5 /// <returns></returns>
 6 public int Fibonacci(int targetNumber)
 7 {
 8 //演算法開始
 9 if (targetNumber <= 0)
10 return 0;
11 if (targetNumber == 1)
12 return 1;
13 return Fibonacci(targetNumber - 1) + Fibonacci(targetNumber - 2);
14 }

得出結果並沒有任何問題。但是這種寫法可靠嗎？是我們想要的嗎？

我們來分析一下為什麼這種寫法會有很嚴重的效率問題。

首先我們求解f(10)，就需要得到f(9)與f(8),想要求解f(9)，勢必要求出f(8)與f(7)，大家看到了嗎？這種重覆求解的關係是很糟糕的，並且會隨著節點數會隨著n的增大而急劇增大。如如下依賴關係圖所示: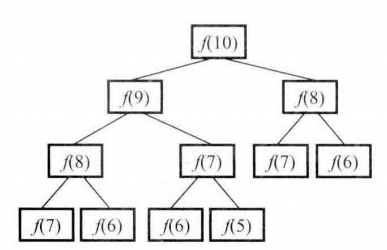

 那我們有沒有更好的寫法呢？當然有，因為遞歸與迴圈本來就是一家人！如下代碼（C#）實例：

/// <summary>
/// 斐波那契數列高級寫法 避免重覆計算
/// </summary>
/// <param name="targerNumber">輸入的目標值</param>
/// <returns></returns>
public int FibonacciPro(int targetNumber)
{
Stopwatch sw = new Stopwatch();
sw.Start();
//演算法開始
int[] arrayBase = {0, 1};
if (targetNumber < 2)
return arrayBase[targetNumber];

int fibNumberOne = 1;
int fibNumberTwo = 0;
int fibCurrentNumber = 0;

for (int i = 2; i <= targetNumber; ++i)
{
fibCurrentNumber = fibNumberOne + fibNumberTwo;
fibNumberTwo = fibNumberOne;
fibNumberOne = fibCurrentNumber;
}

sw.Stop();
TimeSpan ts = sw.Elapsed;
Console.WriteLine("Para is {0},Datatime Costed For Shuffle Function is {1}ms", targetNumber, ts.TotalMilliseconds);
return fibCurrentNumber;
}

寫完了之後我們來看一下性能方面到底是不是節約了很多?

首先，當參數N為10的時候：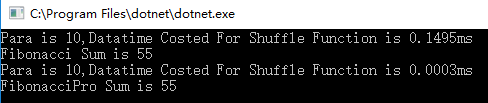

這裡已經可以初步看到效率有了明顯的提升！

當參數N為30的時候，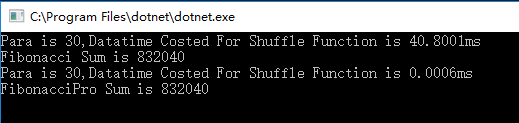

這裡的性能已經有了天翻地覆的差別！

除此之外，第一種方式的遞歸還有可能引起嚴重的棧溢出，每一次調用函數都會在記憶體棧種分配空間，而每個進程的棧容量是有限的，若第一種解法N參數為5000，則運行時候會出錯，但是第二種解法則能得到正確結果。