題目鏈接 FZU - 2295 Human life 題目分析 題意:你在玩一個游戲,在其中你可以通過學習一些技能,但是學習某些技能之前,可能還要學習一些其他的技能,並且學習任何技能都有一定的花費; 而我們可以通過掌握某些工作以獲取報酬,為了掌握這一工作,我們必須學會特定的技能。 不過有些工作彼此之 ...
題目鏈接
題目分析
題意:你在玩一個游戲,在其中你可以通過學習一些技能,但是學習某些技能之前,可能還要學習一些其他的技能,並且學習任何技能都有一定的花費;
而我們可以通過掌握某些工作以獲取報酬,為了掌握這一工作,我們必須學會特定的技能。
不過有些工作彼此之間是衝突的,簡單來說:如果你掌握了工作A,那麼將無法掌握工作B
思路:
由於技能之間也存在依賴關係,但實際上如果要獲取某一工作的報酬,那麼必須選擇這個工作的前置技能以及前置技能的前置技能,
那麼顯然,這些形成依賴關係的技能都是這一工作的前置技能,所以我們的問題就是求最大權閉合子圖了。
我們在工作和其所有的前置技能之間建一條容量為inf的邊,然後由所有的技能向匯點建一條容量為這一技能學習消耗的邊,
再由源點向每個工作建一條容量為這一工作報酬的邊。
這個地方還加上了一個條件,有些工作無法同時獲取,不過這個地方產生衝突最大對數為5個,那麼我們枚舉所有的情況就好了,
一共2^5 = 32種,根據每種狀態來決定可選取的工作,並構建這一頂點及其相關的邊
然後根據:最大閉合子圖的權值 = 所有權值為正的結點的權值之和 - 最小割(最大流)求出答案
順便吐糟一下這個題,首先這個OJ的C++環境不是C11標準,也就是說不支持大括弧給結構體變數賦值,比如這樣:
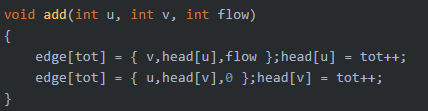
我這個語法寫了近一年了,從未出錯,這個評測機第一次把我這裡卡了,一直CE,還不給出錯誤信息QAQ....
代碼區

#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #include<queue> #include<string> #include<fstream> #include<vector> #include<stack> #include <map> #include <iomanip> #define bug cout << "**********" << endl #define show(x,y) cout<<"["<<x<<","<<y<<"] " //#define LOCAL = 1; using namespace std; typedef long long ll; const int inf = 0x3f3f3f3f; const int mod = 1e9 + 7; const int Max = 1e3+ 10; struct Edge { int to, next, flow; }edge[Max << 2]; int T, n, m, k; int s, t; vector<int>edge_raw[Max]; //記錄原圖邊的關係 int vis[2010][1010]; //vis[i][j]記錄j是否是i的前置結點 int select[2010]; //記錄某點是否被刪除(處理工作衝突) int use[1010]; //記錄每個點的是否使用(處理技能之間的前置關係) int head[2010], tot; int cost[1010]; //記錄了學習每個技能的花費 int val[2010]; //記錄掌握每個工作的報酬 int dis[2010]; //記錄i的層次編號(Dinic中使用) pair<int, int>fight[10]; //記錄衝突 void init() { s = 0, t = n + m + 1; //1-m為技能,m+1~n+m為工作 memset(vis, 0, sizeof(vis)); memset(use, 0, sizeof(use)); for (int i = 0;i <= n; i++) edge_raw[i].clear(); } void add(int u, int v, int flow) { edge[tot].to = v; edge[tot].flow = flow; edge[tot].next = head[u]; head[u] = tot++; edge[tot].to = u; edge[tot].flow = 0; edge[tot].next = head[v]; head[v] = tot++; } void dfs(int u) //找到每個技能所有的前置技能 { use[u] = true; //代表u已經訪問 for (int i = 0; i < edge_raw[u].size(); i++) { int v = edge_raw[u][i]; vis[u][v] = true; if (!use[v]) //自己是自己的前置結點 { dfs(v); } for (int j = 1;j <= n;j++) //枚舉這個點的前置結點 { if (vis[v][j]) //v的前置結點是j,那麼u的前置結點也是j { vis[u][j] = true; } } } } bool bfs() //判斷連通性,將圖分層次 { queue<int>q; memset(dis, -1, sizeof(dis)); dis[s] = 0; q.push(s); while (!q.empty()) { int u = q.front();q.pop(); for (int i = head[u]; i != -1; i = edge[i].next) { int v = edge[i].to; if (dis[v] == -1 && edge[i].flow > 0) { dis[v] = dis[u] + 1; q.push(v); if (v == t) return true; } } } return false; } int dfs(int u, int flow_in) { if (u == t) return flow_in; int flow_out = 0; //實際流出流量 for (int i = head[u];i != -1;i = edge[i].next) { int v = edge[i].to; if (dis[v] == dis[u] + 1 && edge[i].flow > 0) { int flow_part = dfs(v, min(flow_in, edge[i].flow)); if (flow_part == 0)continue; //無法形成增廣路 flow_in -= flow_part; flow_out += flow_part; edge[i].flow -= flow_part; edge[i ^ 1].flow += flow_part; if (flow_in == 0)break; } } return flow_out; } int max_flow() { int sum = 0; while (bfs()) { sum += dfs(s, inf); } return sum; } int main() { #ifdef LOCAL freopen("input.txt", "r", stdin); freopen("output.txt", "w", stdout); #endif scanf("%d", &T); while (T--) { scanf("%d%d%d", &n, &m, &k); init(); for (int i = 1, num;i <= n;i++) { scanf("%d%d", cost + i, &num); for (int j = 1;j <= num;j++) { int pre; //技能i的前置技能點 scanf("%d", &pre); edge_raw[i].push_back(pre); //構建直系前置技能關係 } } for (int i = 1;i <= n;i++) { if (!use[i])dfs(i); } for (int i = n + 1, cnt; i <= n + m;i++) //工作編號n +1 ~n+m { scanf("%d%d", val + i, &cnt); while (cnt--) { int x; scanf("%d", &x); vis[i][x] = true; for (int j = 1;j <= n;j++) { if (vis[x][j]) //求出工作所有的前置技能 vis[i][j] = true; } } } for (int i = 0;i < k;i++) { scanf("%d %d", &fight[i].first, &fight[i].second); } int max_val = 0; for (int state = 0;state < (1 << k);state++) //枚舉狀態,對應位置為1表示選first,0表示選second { memset(select, 0, sizeof(select)); //0表示不刪除 memset(head, -1, sizeof(head));tot = 0; for (int i = 0;i < k;i++) { if ((state >> i) & 1) { select[fight[i].second] = true; //刪除second } else { select[fight[i].first] = true; //刪除first } } int sum = 0; //記錄總價值 for (int i = 1 + n;i <= n + m;i++) { if (select[i - n])continue; //當前狀態下不不選取的工作就不用構建與之有關的邊了 sum += val[i]; add(s, i, val[i]); //由源點向可選工作構建一條容量為當前工作報酬的邊 for (int j = 1;j <= n;j++) { if (vis[i][j]) { add(i, j, inf); //有工作向其所有前置技能點建一條容量為inf的邊 } } } for (int i = 1;i <= n;i++) //由所有技能向匯點構建一條容量為其花費的邊 { add(i, t, cost[i]); } int flow = max_flow(); max_val = max(max_val, sum - flow); //最大閉合子圖的權值 = 所有權值為正的結點的權值之和 - 最小割(最大流) } printf("%d\n", max_val); } return 0; }FZU 2295




