本文為原創？？？

作者寫這篇文章的時候剛剛初一畢業……

如有錯誤請各位大佬指正

從例題入手

洛谷P3915[HNOI2008]玩具裝箱toy

Step0：讀題

Q：暴力？

如果您學習過dp

不難推出dp方程

設dp[i]表示放置前i個物品需要的最小價值

dp[i]=min(dp[j]+(sum[i]-sum[j-1]+i-j-L)^2)

sum[i]表示首碼和

暴力分有了！！恭喜！

下麵我們引入斜率優化：

首先進行一個變形：

原來的式子可以變為：f[i]=min(f[j]+(sum[i]-sum[j]+i-j-L-1)^2)

令a[i]=sum[i]+i,b[i]=sum[i]+i+L+1

f[i]=min(f[j]+(a[i]-b[j])^2)

f[i]=min(f[j]+a[i]^2+b[j]^2-2*a[i]*b[j])     初一公式！展開平方！

把b[j]看做x，f[j]+b[j]^2看做y

y=2*a[i]x+dp[i]-a[i]^2

這就是一條是直線的解析式！

y=kx+b,k=2*a[i],b=f[i]-a[i]^2

要找到一個點P(b[j],f[j]+b[j]^2)使得上面的斜率為2*a[i]的直線穿過這個點且與y 的軸截距最小

因為斜率k=2*a[i]是固定的，所以要求的就是最小的b，加上a[i]^2就是dp[i]的值。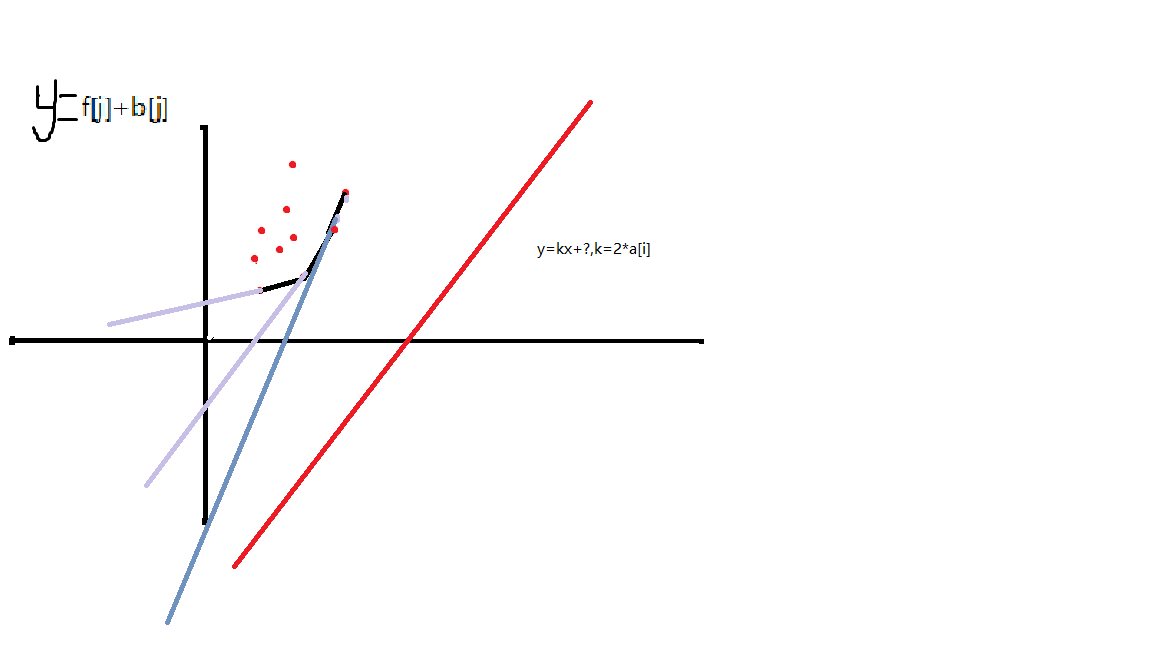

 很明顯就是維護一個下凸殼

令a[i]=sum[i]+i

斜率單調遞增！

code：推薦照著講解看

#include<bits/stdc++.h>
#define ll long long
#define inf 0x7fffffff
#define un unsigned
#define ull un ll
#define int ull
using namespace std;
#define maxn 50009
int n,l,a[maxn];
int f[maxn],g[maxn];
int q[maxn];
int Q(int x){return x*x;}
double Get(un j,un k)//求斜率 
{
    return ((f[j]+Q(g[j])+2*l*g[j])-(f[k]+Q(g[k])+2*l*g[k]))/(double)(g[j]-g[k]);
}
signed main()
{
    scanf("%llu%llu",&n,&l);
    l++;
    int s=1,t=1;
    int K;
    q[s]=0;
    for(int i=1;i<=n;i++)
    {
        scanf("%llu",&g[i]);
        g[i]=g[i]+g[i-1];
    }
    for(int i=1;i<=n;i++)g[i]+=i;
    for(int i=1;i<=n;q[++t]=i++)
    {
        K=g[i]<<1;
        while(s<t&&Get(q[s+1],q[s])<=K) s++;
        int j=q[s];
        f[i]=f[j]+Q(g[i]-g[j]-l);
        while(s<t&&Get(q[t],q[t-1])>=Get(i,q[t]))t--;
    }
    printf("%llu\n",f[n]);
    return 0;
}