圖解數據結構樹之AVL樹_ZenDei技術網路在線

AVL樹(平衡二叉樹)： AVL樹本質上是一顆二叉查找樹，但是它又具有以下特點：它是一棵空樹或它的左右兩個子樹的高度差的絕對值不超過1，並且左右兩個子樹都是一棵平衡二叉樹。在AVL樹中任何節點的兩個子樹的高度最大差別為一，所以它也被稱為平衡二叉樹。下麵是平衡二叉樹和非平衡二叉樹對比的例圖：平衡因數 ...

AVL樹(平衡二叉樹)：

AVL樹本質上是一顆二叉查找樹，但是它又具有以下特點：它是一棵空樹或它的左右兩個子樹的高度差的絕對值不超過1，並且左右兩個子樹都是一棵平衡二叉樹。在AVL樹中任何節點的兩個子樹的高度最大差別為一，所以它也被稱為平衡二叉樹。下麵是平衡二叉樹和非平衡二叉樹對比的例圖：

平衡因數(bf)：結點的左子樹的深度減去右子樹的深度，那麼顯然-1<=bf<=1;

AVL樹的作用：

我們知道，對於一般的二叉搜索樹（Binary Search Tree），其期望高度（即為一棵平衡樹時）為log2n，其各操作的時間複雜度（O(log2n)）同時也由此而決定。但是，在某些極端的情況下（如在插入的序列是有序的時），二叉搜索樹將退化成近似鏈或鏈，此時，其操作的時間複雜度將退化成線性的，即O(n)。我們可以通過隨機化建立二叉搜索樹來儘量的避免這種情況，但是在進行了多次的操作之後，由於在刪除時，我們總是選擇將待刪除節點的後繼代替它本身，這樣就會造成總是右邊的節點數目減少，以至於樹向左偏沉。這同時也會造成樹的平衡性受到破壞，提高它的操作的時間複雜度。

例如：我們按順序將一組數據1,2,3,4,5,6分別插入到一顆空二叉查找樹和AVL樹中，插入的結果如下圖：

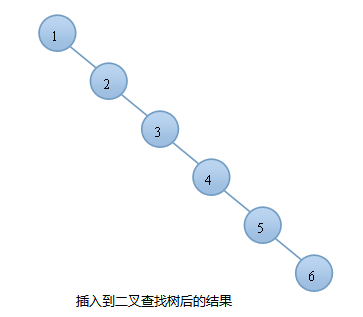
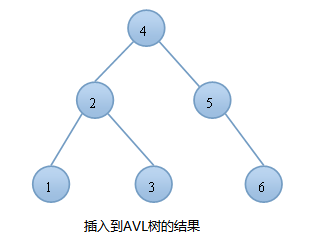
由上圖可知，同樣的結點，由於插入方式不同導致樹的高度也有所不同。特別是在帶插入結點個數很多且正序的情況下，會導致二叉樹的高度是O(N)，而AVL樹就不會出現這種情況，樹的高度始終是O(lgN).高度越小，對樹的一些基本操作的時間複雜度就會越小。這也就是我們引入AVL樹的原因

AVL樹的基本操作：

AVL樹的操作基本和二叉查找樹一樣，這裡我們關註的是兩個變化很大的操作：插入和刪除！

我們知道，AVL樹不僅是一顆二叉查找樹，它還有其他的性質。如果我們按照一般的二叉查找樹的插入方式可能會破壞AVL樹的平衡性。同理，在刪除的時候也有可能會破壞樹的平衡性，所以我們要做一些特殊的處理，包括：單旋轉和雙旋轉！

AVL樹的插入，單旋轉的第一種情況---右旋：

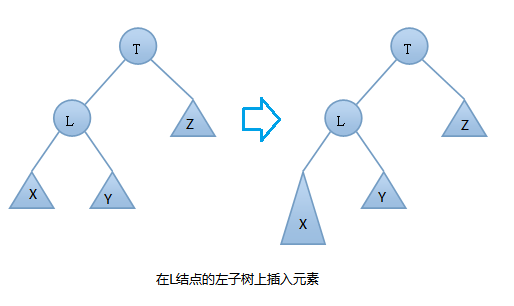
由上圖可知：在插入之前樹是一顆AVL樹，而插入之後結點T的左右子樹高度差的絕對值不再 < 1,此時AVL樹的平衡性被破壞，我們要對其進行旋轉。由上圖可知我們是在結點T的左結點的左子樹上做了插入元素的操作，我們稱這種情況為左左情況，我們應該進行右旋轉(只需旋轉一次，故是單旋轉)。具體旋轉步驟是：

T向右旋轉成為L的右結點，同時，Y放到T的左孩子上。這樣即可得到一顆新的AVL樹，旋轉過程圖如下：

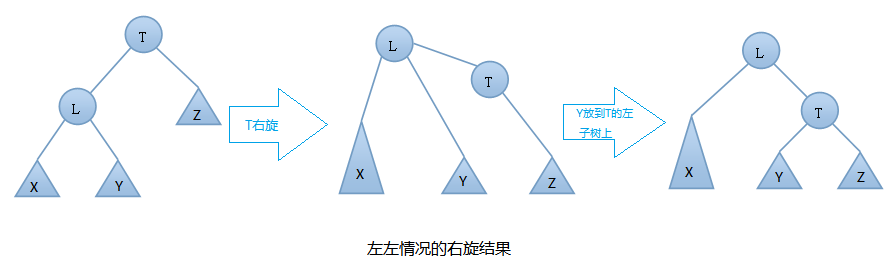
左左情況的右旋舉例：

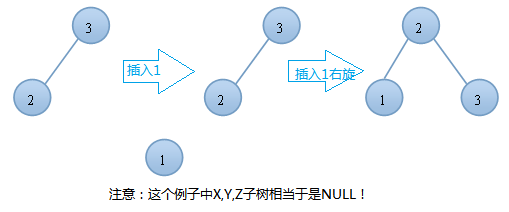
AVL樹的插入，單旋轉的第一種情況---左旋：

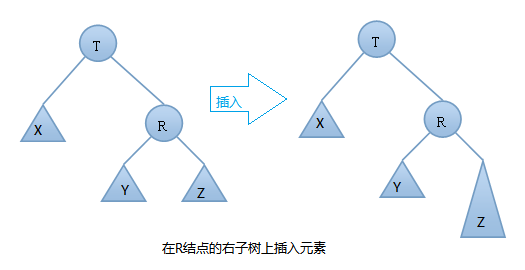
由上圖可知：在插入之前樹是一顆AVL樹，而插入之後結點T的左右子樹高度差的絕對值不再 < 1,此時AVL樹的平衡性被破壞，我們要對其進行旋轉。由上圖可知我們是在結點T的右結點的右子樹上做了插入元素的操作，我們稱這種情況為右右情況，我們應該進行左旋轉(只需旋轉一次，故事單旋轉)。具體旋轉步驟是：

T向右旋轉成為R的左結點，同時，Y放到T的左孩子上。這樣即可得到一顆新的AVL樹，旋轉過程圖如下：

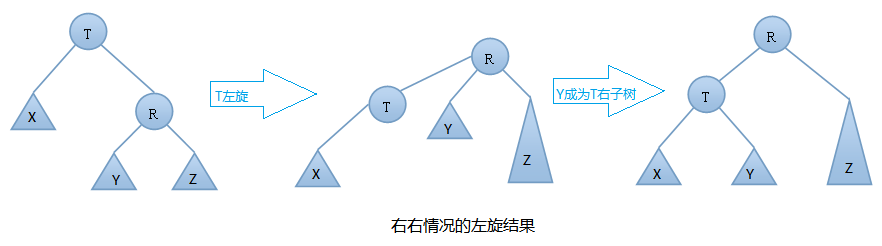
右右情況的左旋舉例：

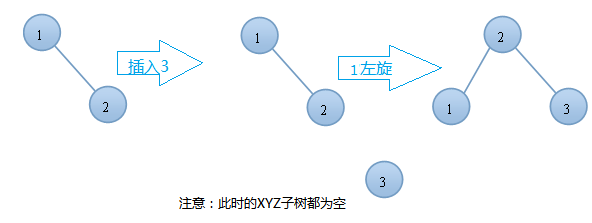
以上就是插入操作時的單旋轉情況！我們要註意的是：誰是T誰是L，誰是R還有誰是X,Y,Z!T始終是開始不平衡的左右子樹的根節點。顯然L是T的左結點，R是T的右節點。X、Y、Y是子樹當然也可以為NULL.NULL歸NULL，但不能破壞插入時我上面所說的左左情況或者右右情況。

AVL樹的插入，雙旋轉的第一種情況---左右(先左後右)旋：

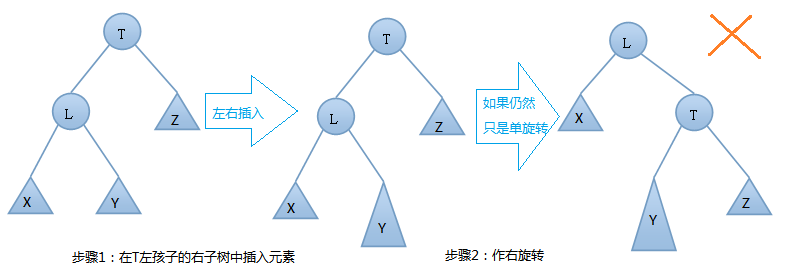
由　　上圖可知，我們在T結點的左結點的右子樹上插入一個元素時，會使得根為T的樹的左右子樹高度差的絕對值不再 < 1，如果只是進行簡單的右旋，得到的樹仍然是不平衡的。我們應該按照如下圖所示進行二次旋轉：

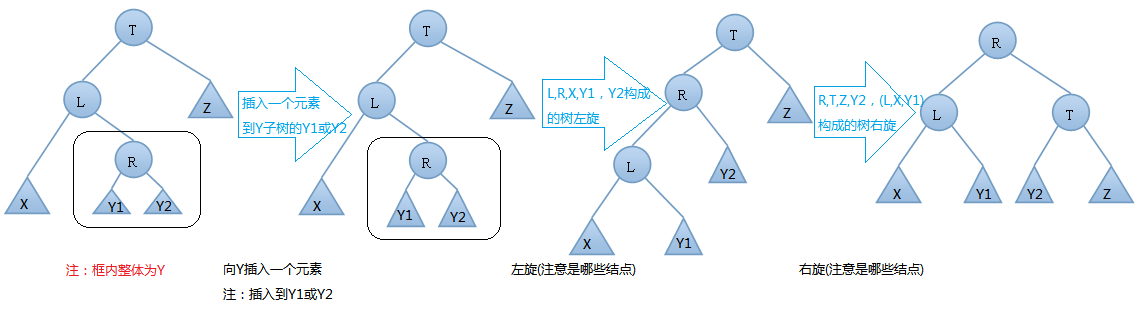
左右情況的左右旋轉實例：

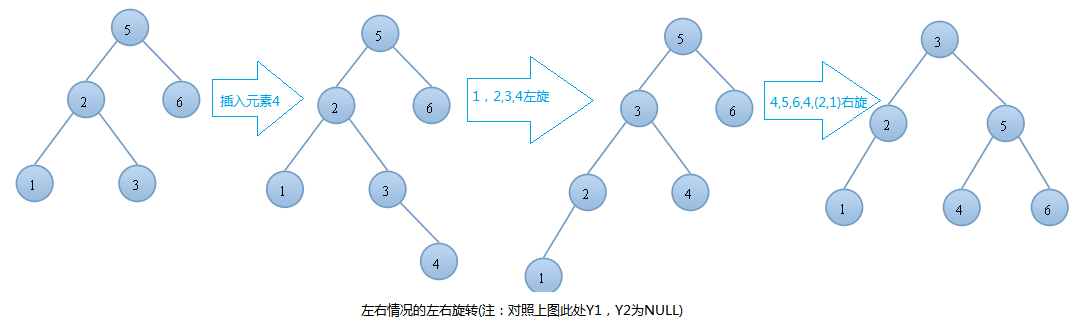
AVL樹的插入，雙旋轉的第二種情況---右左(先右後左)旋：

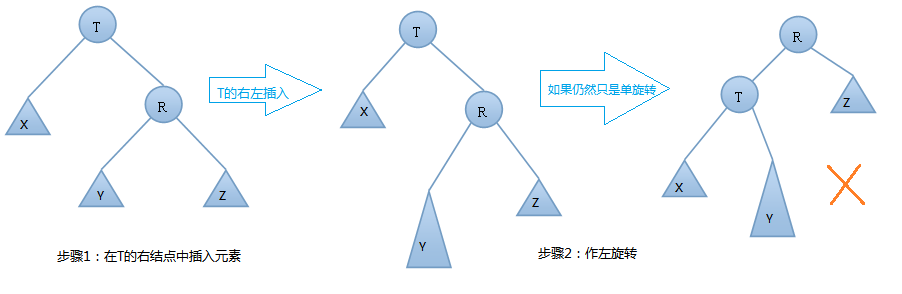
由上圖可知，我們在T結點的右結點的左子樹上插入一個元素時，會使得根為T的樹的左右子樹高度差的絕對值不再 < 1，如果只是進行簡單的左旋，得到的樹仍然是不平衡的。我們應該按照如下圖所示進行二次旋轉：

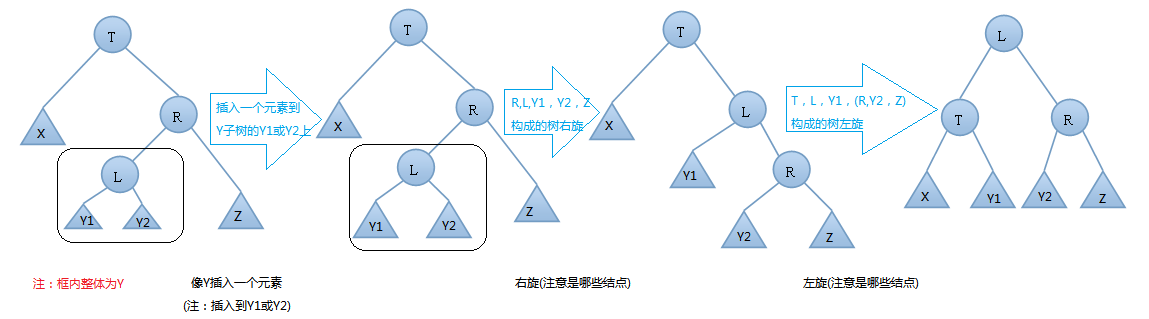
右左情況的右左旋轉實例：

AVL樹的插入代碼實現:(僅供參考)

懂了以上單旋轉和雙旋轉的原理之後，那麼代碼寫起來也就比較簡單了，以下是我寫的代碼，如果有錯還望大家不吝指正。（參考數據結構與演算法分析-Weiss著）

#include <iostream>
#include <stdlib.h>

using namespace std;

#define DataType int

/*
    定義AVL樹的結構體，鏈式
*/
typedef struct AvlNode{
    DataType    data;
    AvlNode    * m_pLeft;
    AvlNode    * m_pRight;
    int height;
}*AvlTree,*Position,AvlNode;

//求兩個數的最大值
int Max(int a,int b)
{
    return a>b?a:b;
}
//求樹的高度
int Height( AvlTree T)
{
    if(NULL == T)
        return -1;
    else
        return T->height;
}

//單旋轉右旋
AvlTree singleRotateWithRight(AvlTree T)
{
    AvlTree L = T->m_pLeft;
    T->m_pLeft = L->m_pRight;
    L->m_pRight = T;
    T->height = Max( Height(T->m_pLeft),Height(T->m_pRight) ) + 1;
    L->height = Max( Height(L->m_pLeft),Height(L->m_pRight) ) + 1;
    return L;    //此時L成為根節點了（可參考AVL的插入的左左情況的右旋圖）
}
//單旋轉左旋
AvlTree singleRotateWithLeft(AvlTree T)
{
    AvlTree R = T->m_pRight;
    T->m_pRight = R->m_pLeft;
    R->m_pLeft = T;
    T->height = Max( Height(T->m_pLeft),Height(T->m_pRight) ) + 1;
    R->height = Max( Height(R->m_pLeft),Height(R->m_pRight) ) + 1;
    return R;    //此時R成為根節點了（可參考AVL的插入的左左情況的左旋圖）
}
//雙旋轉，先左後右
AvlTree doubleRotateWithLeft(AvlTree T)        //先左後右
{
    T->m_pLeft = singleRotateWithLeft(T->m_pLeft);
    return singleRotateWithRight(T);
}
//雙旋轉，先右後左
AvlTree doubleRotateWithRight(AvlTree T)    //先右後左
{
    T->m_pRight = singleRotateWithRight(T->m_pRight);
    return singleRotateWithLeft(T);
}
AvlTree AvlTreeInsert(AvlTree T, DataType x)
{
    if(T == NULL)    //如果樹為空
    {
        T = (AvlNode *)malloc(sizeof(struct AvlNode));
        if(T)
        {
            T->data = x;
            T->m_pLeft    = NULL;
            T->m_pRight = NULL;
            T->height = 0;
        }
        else
        {
            cout << "空間不夠" << endl;
            exit(0);
        }
    }
    else if( x < T->data)        //如果插入到T結點的左子樹上
    {
        T->m_pLeft = AvlTreeInsert(T->m_pLeft,x);    //先插入，後旋轉
        if(Height(T->m_pLeft) - Height(T->m_pRight) == 2) //只有可能是這個
        {
            if(x < T->m_pLeft->data)        //左左情況，只需要右旋轉
            {
                T = singleRotateWithRight( T );
            }
            else                            //左右情況，雙旋轉,先左
            {
                T = doubleRotateWithLeft( T );
            }
        }
    }
    else if( x > T->data )
    {
        T->m_pRight = AvlTreeInsert(T->m_pRight,x);
        if(Height(T->m_pRight) - Height(T->m_pLeft) == 2)
        {
            if(x > T->m_pRight->data)        //右右情況，進行左旋
            {
                T = singleRotateWithLeft( T );
            }
            else                            //左右情況，雙旋轉,先右
            {
                T = doubleRotateWithRight( T );
            }
        }
    }
    //如果這個數已經存在，那麼不進行插入
    T->height = Max(Height(T->m_pLeft),Height(T->m_pRight)) + 1;
    return T;
}
//遞歸實現中序遍歷
void inOrderVisitUseRecur(const AvlTree pCurrent)
{
    if(pCurrent)
    {
        inOrderVisitUseRecur(pCurrent->m_pLeft);
        cout << pCurrent->data << " ";
        if(pCurrent->m_pLeft)
            cout << " leftChild: "<<pCurrent->m_pLeft->data;
        else
            cout << " leftChild: "<<"NULL" ;
        if(pCurrent->m_pRight)
            cout << " rightChild: "<<pCurrent->m_pRight->data;
        else
            cout << " rightChild: "<< "NULL";
        cout << endl;
        inOrderVisitUseRecur(pCurrent->m_pRight);
    }
}
int main()
{
    AvlTree root = NULL;
    root = AvlTreeInsert(root,1);
    root = AvlTreeInsert(root,2);
    root = AvlTreeInsert(root,3);
    root = AvlTreeInsert(root,4);
    root = AvlTreeInsert(root,5);
    root = AvlTreeInsert(root,6);
    root = AvlTreeInsert(root,7);
    root = AvlTreeInsert(root,8);
    root = AvlTreeInsert(root,9);
    root = AvlTreeInsert(root,10);
    root = AvlTreeInsert(root,11);
    root = AvlTreeInsert(root,12);
    root = AvlTreeInsert(root,13);
    root = AvlTreeInsert(root,14);
    root = AvlTreeInsert(root,15);
    inOrderVisitUseRecur(root);
    return 0;
}