1、冒泡排序法(Bubble Sort) 比較相鄰的元素。如果第一個比第二個大,就交換它們兩個; 對每一對相鄰元素作同樣的工作,從開始第一對到結尾的最後一對,這樣在最後的元素應該會是最大的數; 針對所有的元素重覆以上的步驟,除了最後一個; 重覆步驟1~3,直到排序完成。 2、快速排序法(Quick ...
1、冒泡排序法(Bubble Sort)
- 比較相鄰的元素。如果第一個比第二個大,就交換它們兩個;
- 對每一對相鄰元素作同樣的工作,從開始第一對到結尾的最後一對,這樣在最後的元素應該會是最大的數;
- 針對所有的元素重覆以上的步驟,除了最後一個;
- 重覆步驟1~3,直到排序完成。

def BubbleSort(lst): n=len(lst) if n<=1: return lst for i in range (0,n): for j in range(0,n-i-1): if lst[j]>lst[j+1]: (lst[j],lst[j+1])=(lst[j+1],lst[j]) return lst
2、快速排序法(Quick Sort)
- 從數列中挑出一個元素,稱為 “基準”(pivot);
- 重新排序數列,所有元素比基準值小的擺放在基準前面,所有元素比基準值大的擺在基準的後面(相同的數可以到任一邊)。在這個分區退出之後,該基準就處於數列的中間位置。這個稱為分區(partition)操作;
- 遞歸地(recursive)把小於基準值元素的子數列和大於基準值元素的子數列排序。

def QuickSort(lst): # 此函數完成分區操作 def partition(arr, left, right): key = left # 劃分參考數索引,預設為第一個數為基準數,可優化 while left < right: # 如果列表後邊的數,比基準數大或相等,則前移一位直到有比基準數小的數出現 while left < right and arr[right] >= arr[key]: right -= 1 # 如果列表前邊的數,比基準數小或相等,則後移一位直到有比基準數大的數出現 while left < right and arr[left] <= arr[key]: left += 1 # 此時已找到一個比基準大的書,和一個比基準小的數,將他們互換位置 (arr[left], arr[right]) = (arr[right], arr[left]) # 當從兩邊分別逼近,直到兩個位置相等時結束,將左邊小的同基準進行交換 (arr[left], arr[key]) = (arr[key], arr[left]) # 返回目前基準所在位置的索引 return left def quicksort(arr, left, right): if left >= right: return # 從基準開始分區 mid = partition(arr, left, right) # 遞歸調用 # print(arr) quicksort(arr, left, mid - 1) quicksort(arr, mid + 1, right) # 主函數 n = len(lst) if n <= 1: return lst quicksort(lst, 0, n - 1) return lst
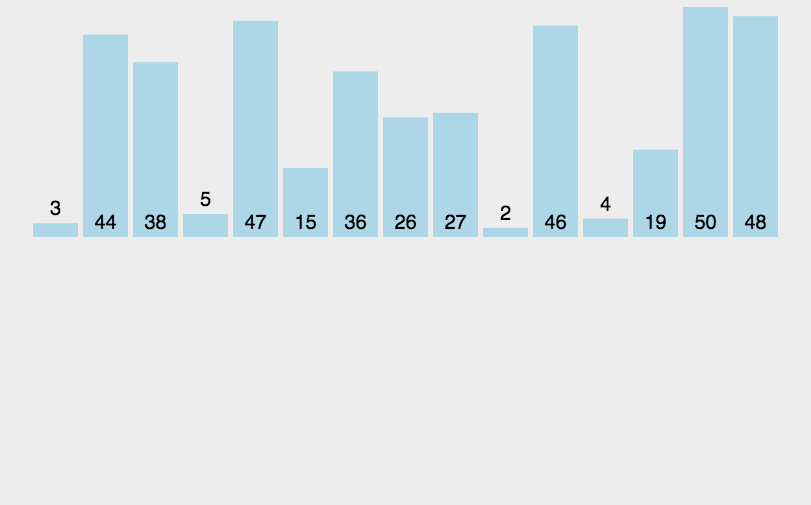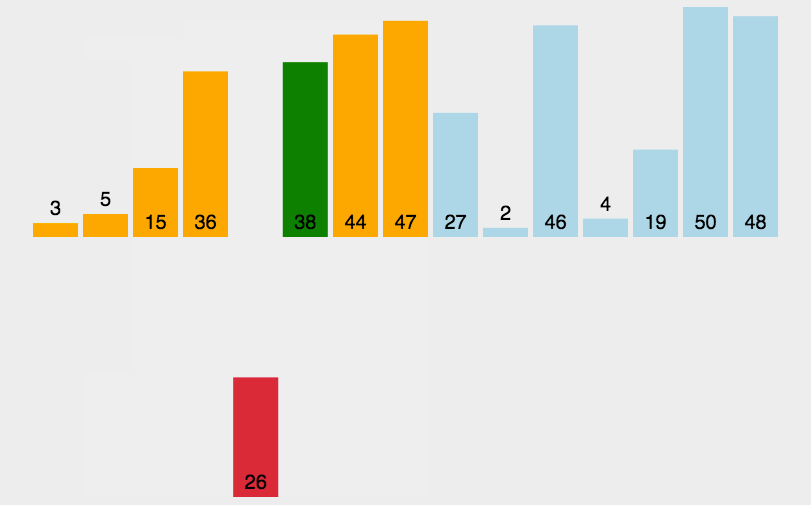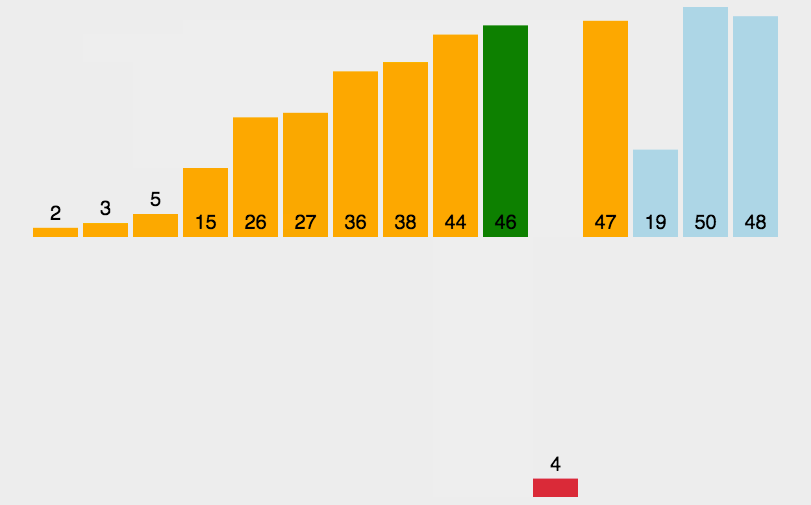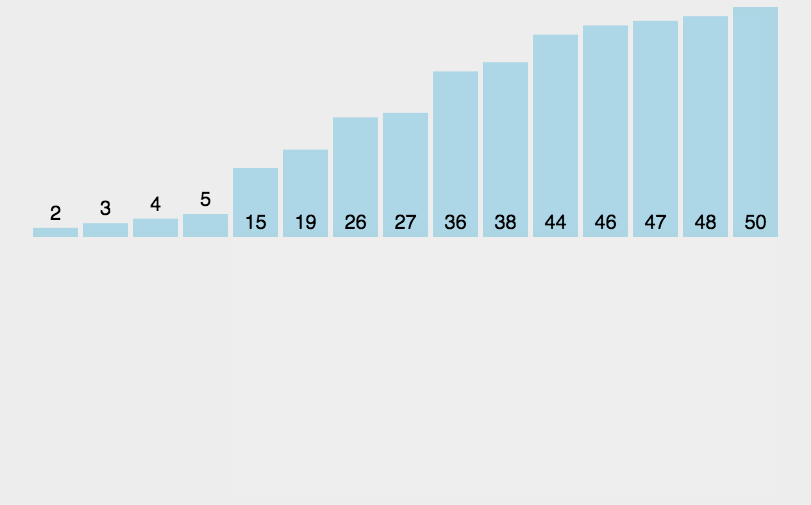
3、插入排序(Insert Sort)
- 從第一個元素開始,該元素可以認為已經被排序;
- 取出下一個元素,在已經排序的元素序列中從後向前掃描;
- 如果該元素(已排序)大於新元素,將該元素移到下一位置;
- 重覆步驟3,直到找到已排序的元素小於或者等於新元素的位置;
- 將新元素插入到該位置後;
- 重覆步驟2~5。
def InsertSort(lst): n=len(lst) if n<=1: return lst for i in range(1,n): j=i target=lst[i] #每次迴圈的一個待插入的數 while j>0 and target<lst[j-1]: #比較、後移,給target騰位置 lst[j]=lst[j-1] j=j-1 lst[j]=target #把target插到空位 return lst
4、希爾排序法(Shell Sort)
- 選擇一個增量序列t1,t2,…,tk,其中ti>tj,tk=1;
- 按增量序列個數k,對序列進行k 趟排序;
- 每趟排序,根據對應的增量ti,將待排序列分割成若幹長度為m 的子序列,分別對各子表進行直接插入排序。僅增量因數為1 時,整個序列作為一個表來處理,表長度即為整個序列的長度。

def ShellSort(lst): def shellinsert(arr,d): n=len(arr) for i in range(d,n): j=i-d temp=arr[i] #記錄要出入的數 while(j>=0 and arr[j]>temp): #從後向前,找打比其小的數的位置 arr[j+d]=arr[j] #向後挪動 j-=d if j!=i-d: arr[j+d]=temp n=len(lst) if n<=1: return lst d=n//2 while d>=1: shellinsert(lst,d) d=d//2 return lst
5、選擇排序法(Select Sort)
- 初始狀態:無序區為R[1..n],有序區為空;
- 第i趟排序(i=1,2,3…n-1)開始時,當前有序區和無序區分別為R[1..i-1]和R(i..n)。該趟排序從當前無序區中-選出關鍵字最小的記錄 R[k],將它與無序區的第1個記錄R交換,使R[1..i]和R[i+1..n)分別變為記錄個數增加1個的新有序區和記錄個數減少1個的新無序區;
- n-1趟結束,數組有序化了。

def SelectSort(lst): n = len(lst) if n<=1: return lst for i in range(0,n-1): minIndex = i for j in range(i+1,n): #比較一遍,記錄索引不交換 if lst[j]<lst[minIndex]: minIndex=j if minIndex!=i: (lst[minIndex],lst[i])=(lst[i],lst[minIndex]) return lst
6、堆積排序法(Heap Sort)
- 將初始待排序關鍵字序列(R1,R2….Rn)構建成大頂堆,此堆為初始的無序區;
- 將堆頂元素R[1]與最後一個元素R[n]交換,此時得到新的無序區(R1,R2,……Rn-1)和新的有序區(Rn),且滿足R[1,2…n-1]<=R[n];
- 由於交換後新的堆頂R[1]可能違反堆的性質,因此需要對當前無序區(R1,R2,……Rn-1)調整為新堆,然後再次將R[1]與無序區最後一個元素交換,得到新的無序區(R1,R2….Rn-2)和新的有序區(Rn-1,Rn)。不斷重覆此過程直到有序區的元素個數為n-1,則整個排序過程完成

def HeapSort(lst): def heapadjust(arr,start,end): #將以start為根節點的堆調整為大頂堆 temp=arr[start] son=2*start+1 while son<=end: if son<end and arr[son]<arr[son+1]: #找出左右孩子節點較大的 son+=1 if temp>=arr[son]: #判斷是否為大頂堆 break arr[start]=arr[son] #子節點上移 start=son #繼續向下比較 son=2*son+1 arr[start]=temp #將原堆頂插入正確位置 ####### n=len(lst) if n<=1: return lst #建立大頂堆 root=n//2-1 #最後一個非葉節點(完全二叉樹中) while(root>=0): heapadjust(lst,root,n-1) root-=1 #掐掉堆頂後調整堆 i=n-1 while(i>=0): (lst[0],lst[i])=(lst[i],lst[0]) #將大頂堆堆頂數放到最後 heapadjust(lst,0,i-1) #調整剩餘數組成的堆 i-=1 return lst
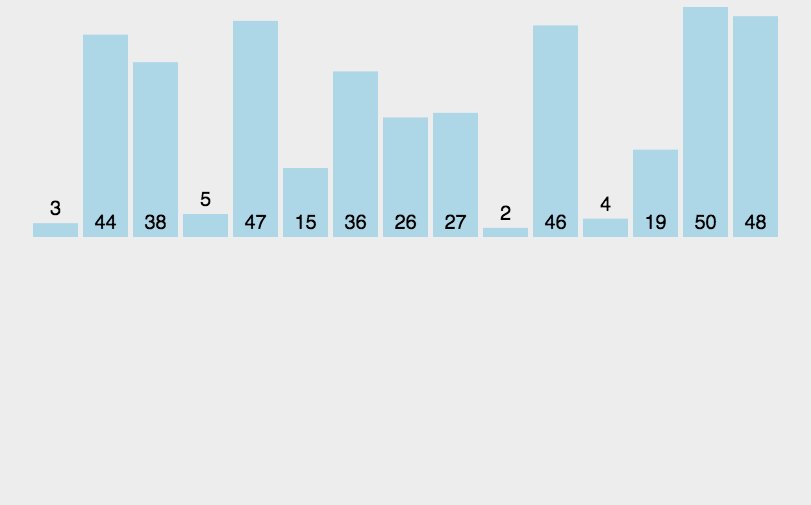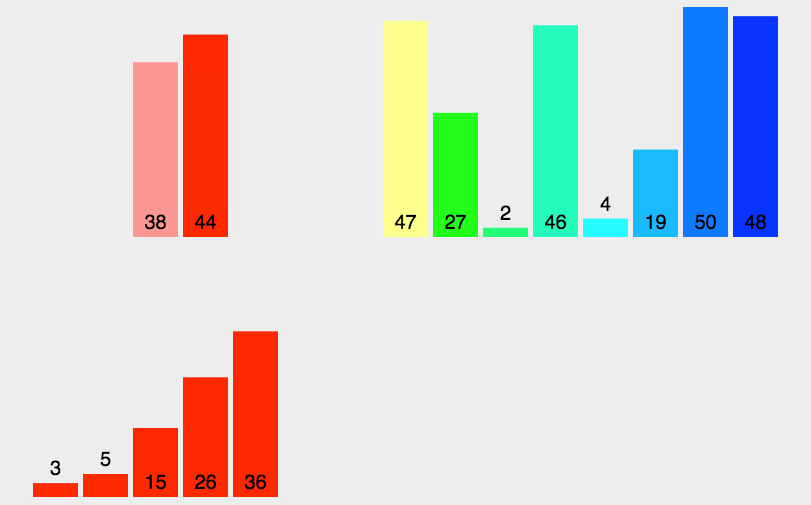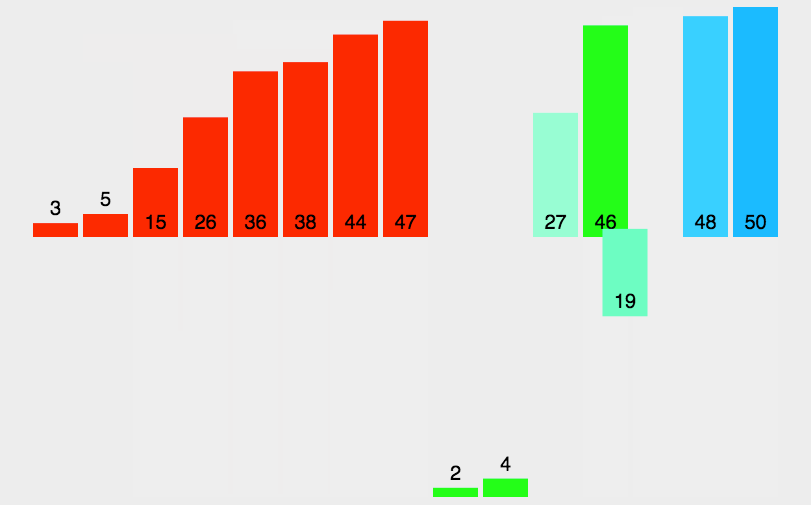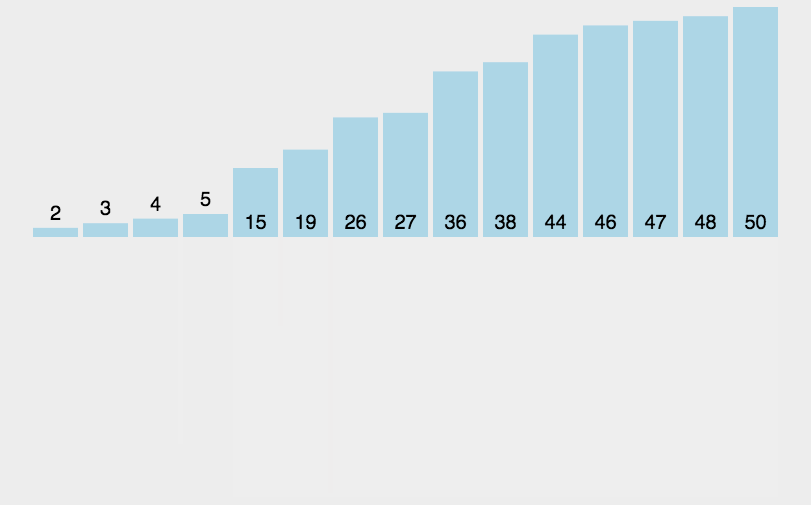
7、歸併排序法(Merge Sort)
- 把長度為n的輸入序列分成兩個長度為n/2的子序列;
- 對這兩個子序列分別採用歸併排序;
- 將兩個排序好的子序列合併成一個最終的排序序列
def MergeSort(lst): #合併左右子序列函數 def merge(arr,left,mid,right): temp=[] #中間數組 i=left #左段子序列起始 j=mid+1 #右段子序列起始 while i<=mid and j<=right: if arr[i]<=arr[j]: temp.append(arr[i]) i+=1 else: temp.append(arr[j]) j+=1 while i<=mid: temp.append(arr[i]) i+=1 while j<=right: temp.append(arr[j]) j+=1 for i in range(left,right+1): # !註意這裡,不能直接arr=temp,他倆大小都不一定一樣 arr[i]=temp[i-left] #遞歸調用歸併排序 def mSort(arr,left,right): if left>=right: return mid=(left+right)//2 mSort(arr,left,mid) mSort(arr,mid+1,right) merge(arr,left,mid,right) n=len(lst) if n<=1: return lst mSort(lst,0,n-1) return lst
8、基數排序法(Radix Sort)
- 取得數組中的最大數,並取得位數;
- arr為原始數組,從最低位開始取每個位組成radix數組;
- 對radix進行計數排序(利用計數排序適用於小範圍數的特點);

import math def RadixSort(lst): def getbit(x,i): #返回x的第i位(從右向左,個位為0)數值 y=x//pow(10,i) z=y%10 return z def CountSort(lst): n=len(lst) num=max(lst) count=[0]*(num+1) for i in range(0,n): count[lst[i]]+=1 arr=[] for i in range(0,num+1): for j in range(0,count[i]): arr.append(i) return arr Max=max(lst) for k in range(0,int(math.log10(Max))+1): #對k位數排k次,每次按某一位來排 arr=[[] for i in range(0,10)] for i in lst: #將ls(待排數列)中每個數按某一位分類(0-9共10類)存到arr[][]二維數組(列表)中 arr[getbit(i,k)].append(i) for i in range(0,10): #對arr[]中每一類(一個列表) 按計數排序排好 if len(arr[i])>0: arr[i]=CountSort(arr[i]) j=9 n=len(lst) for i in range(0,n): #順序輸出arr[][]中數到ls中,即按第k位排好 while len(arr[j])==0: j-=1 else: lst[n-1-i]=arr[j].pop() return lst
轉載鏈接:https://blog.csdn.net/weixin_41571493/article/details/81875088



