長樂培訓Day5

来源:https://www.cnblogs.com/I-Love-You-520/archive/2019/07/26/11252648.html
-Advertisement-
Play Games

T1 圓圈舞蹈 題目 【題目描述】 熊大媽的奶牛在時針的帶領下，圍成了一個圈跳舞。由於沒有嚴格的教育，奶牛們之間的間隔不一致。 奶牛想知道兩隻最遠的奶牛到底隔了多遠。奶牛A到B的距離為A順時針走和逆時針走，到達B的較短路程。 告訴你相鄰個奶牛間的距離，請你告訴奶牛兩隻最遠的奶牛到底隔了多遠。 【輸入 ...


T1 圓圈舞蹈

題目

【題目描述】

熊大媽的奶牛在時針的帶領下，圍成了一個圈跳舞。由於沒有嚴格的教育，奶牛們之間的間隔不一致。

奶牛想知道兩隻最遠的奶牛到底隔了多遠。奶牛A到B的距離為A順時針走和逆時針走，到達B的較短路程。

告訴你相鄰個奶牛間的距離，請你告訴奶牛兩隻最遠的奶牛到底隔了多遠。

【輸入格式】

第一行一個整數N，表示有N只奶牛。

接下來2~N+1行，第I行有一個數，表示第I-1頭奶牛順時針到第I頭奶牛的距離。

第N+1行的數表示第N頭奶牛順時針到第1頭奶牛的距離。

【輸出格式】

一行，表示最大距離。

【數據規模】

2<=N<=100000，

1<=距離<=maxlongint,距離和<=maxlongint。

解析

分析一下題目，多試幾組數據，不難發現，其實我們並不需要知道所有牛之間的距離，

只需要知道對於每頭牛來說，離它最遠的牛有多遠，實際實現時，我們需要求出每頭牛順時針與逆時針離它最遠的牛。

這裡引用一下大佬的解釋：

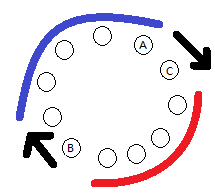
如圖，對於枚舉的第一頭牛A，找到離它最遠的牛B，

當我們沿順時針枚舉第二頭牛C時，離C最遠的牛不可能是圖中紅色區域的牛了，

所以我們只需要將B沿順時針枚舉，當藍色部分的距離小於紅色部分時枚舉停止，

因為此時藍色部分的牛不可能是離C最遠的牛了。

這個演算法是沿著圈繞了一圈，時間複雜度為O(n)，足以AC。

Code

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN = 100005;
int ans, a[MAXN], b[MAXN], n, i, j, k, tot, t;
int main()
{
    //freopen("circle.in", "r", stdin);
    //freopen("circle.out", "w", stdout);
    cin >> n;
    for(i = 1; i <= n; i ++)
        scanf("%d", &a[i]);
    for(i = 1; i <= n; i ++)
        tot += a[i];
    j = 2;
    t = a[1];
    for(i = 1; i <= n; i ++)
    {
        while (min(t, tot - t) <= min(t + a[j], tot - t - a[j]) && j < n) j ++, t += a[j - 1];
        ans = max(ans, min(t, tot - t));
        t -= a[i];
    }
    cout << ans << endl;
    //fclose(stdin); fclose(stdout);
}
View Code

 

 

 

 

 

T2 小麥畝產一千八

題目

【題目描述】

“有了金坷垃，肥料一袋能頂兩袋撒，小麥畝產一千八，吸收兩米下的氮磷鉀……”，話說HYSBZ（Hengyang School for Boys & Zy）學識淵博孩紙們一講到糧食，都會想起印度那個著名的故事：

國王要在第一個格子里放入一粒小麥，接下來的格子放入前面一個格子的兩倍的小麥。這樣所需小麥總數是巨大的，哪是不用金坷垃就能完成的任務？

不過為了減輕國王的任務，那個下棋獲勝的宰相換了一個要求：“我只需要你在棋盤外放一粒小麥，可以將其理解為第0個格子，然後你需要在第一個格子里放入若幹小麥，

之後每一個格子放入前兩個格子的小麥數之和的小麥，並且要滿足第a個格子放x粒小麥，第b個格子放……”說到這，宰相突然發現自己說的滿足第a個格子放x粒小麥的情況可能不存在……

欺君可是大罪啊！國王看到宰相遲遲不說，自己也煩了！我自己來算！於是國王拜托你，讓你算出第b個格子應該放幾粒小麥。當然，就算答案不存在，你也是要告訴國王的。

【輸入格式】

該題有多組數據，請讀到文件末結束。

對於每一組數據僅一行，3個正整數a,x,b,分別表示第a個格子放了x粒小麥，以及你所需要計算的是第b個格子的小麥數量。

【輸出格式】

對於每一次詢問，僅1個整數，為第b個格子的小麥數量，若宰相說的情況不存在，那麼請輸出-1。

【數據規模】

對於50%的數據：如果答案存在，那麼p<=50

對於100%的數據：1<=數據組數<=10000，1<=a,b<=20, 數據保證如果答案存在，那麼1<=p<=1000000.(註:p是第一格放置的小麥數)。

解析

題目明顯給出了一個拓展的斐波那契數列，其滿足：f[0]=1,f[1]=p,f[2]=p+1,f[3]=2*p+1······

而原來的斐波那契數列滿足：F[0]=1,F[1]=1,F[2]=2,F[3]=3······

設g[i]=f[i]-F[i]，則g[0]=0,g[1]=p-1,g[2]=p-1,g[3]=2*p-2,g[4]=3*p-3······

輸入已經給出了f[a]=x，所以g[a]=x-F[a]=F[a-1]*(p-1)，

我們先預處理出F數組，那麼每組數據我們可以O（1）計算出p，

之後遞推出答案就行了，每組數據時間複雜度為O（b）。

Code

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
int a, b;
long long f[30], x;
inline void check(int mid)
{
    f[1] = mid;
    for(int i = 2; i <= a; i ++)
        f[i] = f[i - 1] + f[i - 2];
}
inline void getans(int mid)
{
    f[1] = mid;
    for(int i = 2; i <= b; i ++)
        f[i] = f[i - 1] + f[i - 2];
    printf("%lld\n", f[b]);
}
int main()
{
    //freopen("kela.in", "r", stdin);
    //freopen("kela.out", "w", stdout);return 0； 
    f[0] = 1;
    while (scanf("%d%lld%d", &a, &x, &b) != EOF)
    {
        int l = 1, r = 1000000;
        while (l != r - 1)
        {
            int mid = (l + r) >> 1;
            check(mid);
            if (f[a] > x) r = mid;
            else l = mid; 
        }
        check(l);
        if (f[a] == x) getans(l);
        else {
            check(r); 
            if (f[a] == x) getans(r);
            else printf("-1\n");
        }
    }
    //fclose(stdin); fclose(stdout);
}
View Code

 

 

 

 

 

T3 好元素

題目

【題目描述】

小A一直認為，如果在一個由N個整數組成的數列{An}中，存在以下情況：

Am+An+Ap = Ai (1 <= m, n, p < i <= N ,  m,n,p可以相同)，那麼Ai就是一個好元素。

現在小A有一個數列，請你計算數列中好元素的數目。

【輸入格式】

第一行只有一個正整數N，意義如上。

第二行包含N個整數，表示數列{An}。

【輸出格式】

輸出一個整數，表示這個數列中好元素的個數。

【數據規模】

對於10%的數據1<=N<=10

對於40%的數據1<=N<=500 -10^5<=Ai<=10^5

對於70%的數據1<=N<=5000 -10^6<=Ai<=10^6

對於100%的數據1<=N<=5000 -10^9<=Ai<=10^9

解析

10分做法：四層迴圈枚舉a[i],a[m],a[n],a[p]，時間複雜度O(n4)

40分做法：bool數組存儲a[i]，再三層迴圈a[m],a[n],a[p]，若a[i]存在個數就+1，時間複雜度O(n3)

70分做法：我們發現40分做法計算三數和用了O(n3)，而查詢a[i]只用了O(n)，

我們把代數式轉換為a[m]+a[n]=a[i]-a[p]，這樣計算和查詢都是O(n2)，總時間複雜度為O(n2)

100分做法：在70分演算法的前提下加上哈希進行判斷即可。

Code

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<string>
#include<cmath>
#include<ctime>
#include<queue>
#include<stack>
#include<map>
#include<set>
using namespace std;

const int MAXN=int(5e3)+3;
const int MAXH=int(1e7)+int(3e6);
const int Hash_Value=33554431;
const int MAXV=Hash_Value+1;

int Top,Val[MAXH],Next[MAXH],First[MAXV];
int N,Ans,A[MAXN];

void Push_Hash(const int &x) {
    int Px=x&Hash_Value;
    Next[++Top]=First[Px];
    Val[Top]=x;
    First[Px]=Top;
    return ;
}

bool Ask_Hash(const int &x) {
    int Px=x&Hash_Value;
    for (int k=First[Px];k!=0;k=Next[k])
        if (Val[k]==x) return true;
    return false;
}

int Get() {
    int Sign=0,Num=0;
    char ch;
    for (ch=getchar();ch<'0'||ch>'9';ch=getchar()) if (ch=='-') break;
    ch=='-'?Sign=1:Num=ch-48;
    for (ch=getchar();ch>='0'&&ch<='9';ch=getchar()) Num=Num*10+ch-48;
    return Sign==0?Num:-Num;
}

int main() {
    //freopen("good.in","r",stdin);
    //freopen("good.out","w",stdout);
    N=Get();
    for (int i=1;i<=N;++i) {
        A[i]=Get();
        for (int j=i-1;j>=1;--j) {
            int Now=A[i]-A[j];
            if (Ask_Hash(Now)) {
                ++Ans;
                break;
            }
        }
        for (int j=1;j<=i;++j) {
            int Now=A[i]+A[j];
            Push_Hash(Now);
        }
    }
    printf("%d\n",Ans);
    //fclose(stdin);fclose(stdout);
    return 0;
}
View Code

 

 

 

 

 

T4 國際象棋

題目

【題目描述】

小口口不是一個普通青年，所以他不喜歡玩普通國際象棋。他喜歡玩的國際象棋是這樣的：把兩個邊長分別為 N*N 和 M*M 的國際象棋盤拼在一起。就像這樣：

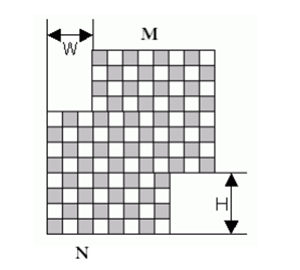
現在小口口又來刁難你了：他告訴你 N,M,W,H 以及 K。

然後問你這樣的棋盤上放 K 個城堡互相不攻擊有多少種方案。

城堡的攻擊範圍是一整行和一整列。

【輸入格式】

第一行，五個整數，分別為 N,M,W,H,K。

【輸出格式】

輸出一行一個整數表示方案總數。

【數據規模】

10%的數據N=M=K.

50%的數據W=H=0,1<=N,M<=15(包括上述的10%的數據).

100%的數據N,M<=20,W,H,K<=10^9.

解析

本蒟蒻表示，這題神馬不會寫，隨便寫了個暴力就溜了。

So，直接拋出巨佬題解：

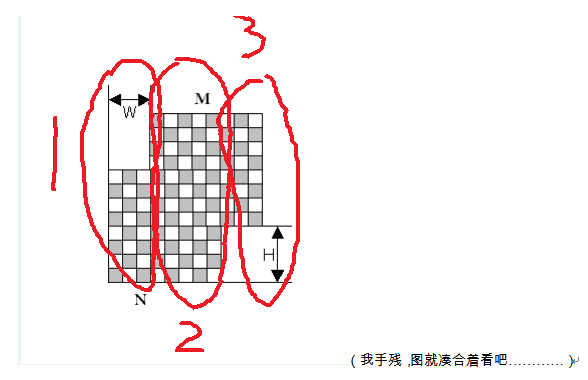
Code

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
int n,m,w,h,k,W,H;
struct ff {
    int len,a[50];
    ff(){ len=0; memset(a,0,sizeof(a)); }
    
    inline ff operator *(const int &b){
        ff c=*this;
        for (int i=1; i<=len; ++i) c.a[i]*=b;
        for (int i=1; i<=len; ++i){
            c.a[i+1]+=c.a[i]/10;
            c.a[i]%=10;
        }
        c.len=len;
        while (c.a[c.len+1]) 
            c.len++, c.a[c.len+1]=c.a[c.len]/10, c.a[c.len]%=10;
        return c;
    }
    inline void operator +=(const ff &b){
        len=max(len,b.len);
        for (int i=1; i<=len; ++i){
            a[i]+=b.a[i];
            a[i+1]+=a[i]/10;
            a[i]%=10;
        }
        while (a[len+1]) ++len, a[len+1]=a[len]/10, a[len]%=10;
    }
}f[45][25][25][25],ans;
void PRT(ff a)
{
    for (int i=a.len; i; --i)
        printf("%d",a.a[i]);
    printf("\n");
}
bool check(int x,int y)
{
    if (x<=n && y<=n) return 1;
    if (x>w && x<=w+m && y>h && y<=h+m) return 1;
    return 0;
}
void work()
{
    if (w>=n) w=n;
    if (h>=n) h=n;
    if (m+w<=n && m+h<=n) w=h=0,m=n;
    
    int H=max(h+m,n),W=max(m+w,n);                                        //H!W!
    int l1=w,l2=min(w+m,n),l3=max(w+m,n);
    int n1=l1,n2=l2-l1,n3=l3-l2;
    f[0][0][0][0].len=1; 
    f[0][0][0][0].a[1]=1;
    for (int i=0; i<H; ++i){    
        for (int x=0; x<=n1; ++x)
        if (x<=k){
            for (int y=0; y<=n2; ++y)
            if (x+y<=k)
              for (int z=0; z<=n3; ++z)
              if (x+y+z<=k){
                    if (check(l1,i+1)){
                        f[i+1][x+1][y][z]+=f[i][x][y][z]*(n1-x);
                    } 
                    if (check(l3,i+1)) f[i+1][x][y][z+1]+=f[i][x][y][z]*(n3-z);
                    if (check(l2,i+1)) f[i+1][x][y+1][z]+=f[i][x][y][z]*(n2-y);
                    f[i+1][x][y][z]+=f[i][x][y][z];
              }
        }
    }
    for (int x=0; x<=n1; ++x)
      for (int y=0; y<=n2; ++y)
        for (int z=0; z<=n3; ++z)
        if (x+y+z==k){        
           ans+=f[H][x][y][z];           
        }
    for (int i=ans.len; i; --i)
        printf("%d",ans.a[i]);
    
}
int main()
{
    //freopen("chess.in","r",stdin);
    //freopen("chess.out","w",stdout);
    scanf("%d%d%d%d%d",&n,&m,&w,&h,&k);    
    work();
    //fclose(stdin); fclose(stdout);
}
View Code
您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • Golang 傳遞任意類型的切片
    肯定有這樣的一種場景，寫一個函數，該函數可以接收任意類型的切片，完成相應的功能。 就好比這種情況 還有很多類型的切片，但是我對這些切片的使用，只是for迴圈每一個元素，執行Print操作就可以了。 那就定義一個函數，函數的接收參數就是這個切片就行了，但是切片類型太多了，你要根據不同的切片類型，寫不同 ...
  • 埃及乘法代碼實現
    什麼是埃及乘法 埃及乘法的思路是：反覆地將n減半，並將a加倍，同時求出a的各種倍數，這些倍數與a的比值都是2的整數次冪。n的值為奇數部分的a之和即為所求值 舉個慄子：41 x 59 1 41 59 √ 2 20 118 4 10 236 8 5 472 √ 16 2 944 32 1 1888 √ ...
  • python3:使用for迴圈列印九九乘法表
    運行結果： 發現乘法表有錯位，在程式中加入製表符，就解決了 程式如下： 運行結果： ...
  • JAVA-註解(2)-自定義註解及反射註解
    自定義註解開發 1.開發一個註解類 開發一個註解類的過程，非常類似於開發一個介面，只不過需要通過@interface關鍵字來聲明 2.使用元註解修飾註解的聲明 所謂的原註解是用來修飾註解聲明的註釋，可以控制被修飾的註解的特性。 @Target 用來聲明被修飾的註解可以用在什麼位置。 可以在@Targ ...
  • Spring Cloud 之 Config與動態路由.
    一、簡介  Spring Cloud Confg 是用來為分散式系統中的基礎設施和微服務應用提供集中化的外部配置支持，它分為服務端與客戶端兩個部分。其中服務端也稱為分散式配置中心，它是一個獨立的微服務應用，用來連接配置倉庫併為客戶端提供獲取配置信息、加密/解密信息等訪問介面；而客戶端則是微 ...
  • Java emoji持久化mysql
    好久沒有更新博客了，今天和大家分享一個關於emoji表情持久化問題，相信做web開發的都遇到過這樣的問題，因為我們知道mysql的utf-8字元集保存不了保存不了表情字元，這是為什麼呢？因為普通的字元串或者表情都是占位3個位元組，所以utf8足夠用了，但是移動端的表情符號占位是4個位元組，普通的utf8 ...
  • Python基礎總結之第五天開始【認識簡單的條件語句，也可以叫判斷語句】（新手可相互督促）
    周五更新很累。。。 堅持，年薪20萬又進了一步~~ python中的條件語句以【 if 】開頭，條件語句成立時，運行該代碼塊，如果條件不成立，則跳過該代碼塊，執行後面的代碼塊。 簡單的小示例： 輸入性別，進行簡單的判斷，用if語句實現代碼。 總結一下： 1、elif語句其實是 else if 的縮寫 ...
  • python 之 併發編程（線程Event、協程）
    9.14 線程Event connect線程執行到event.wait()時開始等待，直到check線程執行event.set()後立即繼續線程connect connect線程執行到event.wait(1)時開始等待1秒，count計數+1，如果到check線程執行event.set()前已經4 ...
一周排行
    -Advertisement-
    Play Games
  • 移動開發（一）：使用.NET MAUI開發第一個安卓APP
    移動開發（一）：使用.NET MAUI開發第一個安卓APP 對於工作多年的C#程式員來說，近來想嘗試開發一款安卓APP，考慮了很久最終選擇使用.NET MAUI這個微軟官方的框架來嘗試體驗開發安卓APP，畢竟是使用Visual Studio開發工具，使用起來也比較的順手，結合微軟官方的教程進行了安卓 ...
  • wpf ToggleButton選中效果和一個登錄界面
    前言 QuestPDF 是一個開源 .NET 庫，用於生成 PDF 文檔。使用了C# Fluent API方式可簡化開發、減少錯誤並提高工作效率。利用它可以輕鬆生成 PDF 報告、發票、導出文件等。 項目介紹 QuestPDF 是一個革命性的開源 .NET 庫，它徹底改變了我們生成 PDF 文檔的方 ...
  • 彈幕樹洞項目功能新增篇
    項目地址 項目後端地址： https://github.com/ZyPLJ/ZYTteeHole 項目前端頁面地址： ZyPLJ/TreeHoleVue (github.com) https://github.com/ZyPLJ/TreeHoleVue 目前項目測試訪問地址： http://tree ...
  • 第27篇 sqlserver2022詳細安裝步驟
    話不多說，直接開乾 一.下載 1.官方鏈接下載： https://www.microsoft.com/zh-cn/sql-server/sql-server-downloads 2.在下載目錄中找到下麵這個小的安裝包 SQL2022-SSEI-Dev.exe，運行開始下載SQL server； 二. ...
  • .NET 開源高性能 MQTT 類庫
    前言 隨著物聯網（IoT）技術的迅猛發展，MQTT（消息隊列遙測傳輸）協議憑藉其輕量級和高效性，已成為眾多物聯網應用的首選通信標準。 MQTTnet 作為一個高性能的 .NET 開源庫，為 .NET 平臺上的 MQTT 客戶端與伺服器開發提供了強大的支持。 本文將全面介紹 MQTTnet 的核心功能 ...
  • Serilog文檔翻譯系列（六） - 可用的接收器、增強器、格式化輸出
    Serilog支持多種接收器用於日誌存儲，增強器用於添加屬性，LogContext管理動態屬性，支持多種輸出格式包括純文本、JSON及ExpressionTemplate。還提供了自定義格式化選項，適用於不同需求。 ...
  • 警惕 Visual Studio 屬性求值副作用導致邏輯不符合預期
    目錄簡介獲取 HTML 文檔解析 HTML 文檔測試參考文章 簡介 動態內容網站使用 JavaScript 腳本動態檢索和渲染數據，爬取信息時需要模擬瀏覽器行為，否則獲取到的源碼基本是空的。 本文使用的爬取步驟如下： 使用 Selenium 獲取渲染後的 HTML 文檔 使用 HtmlAgility ...
  • [使用目前最新版]HybridCLR6.9.0+YooAsset2.2.4實現純C# Unity熱更新方案 (一)
    1.前言 什麼是熱更新 游戲或者軟體更新時，無需重新下載客戶端進行安裝，而是在應用程式啟動的情況下，在內部進行資源或者代碼更新 Unity目前常用熱更新解決方案 HybridCLR，Xlua，ILRuntime等 Unity目前常用資源管理解決方案 AssetBundles，Addressable， ...
  • 在 ASP.NET Core Web API 中使用操作篩選器統一處理通用操作
    本文章主要是在C# ASP.NET Core Web API框架實現向手機發送驗證碼簡訊功能。這裡我選擇是一個互億無線簡訊驗證碼平臺，其實像阿裡雲，騰訊雲上面也可以。 首先我們先去 互億無線 https://www.ihuyi.com/api/sms.html 去註冊一個賬號 註冊完成賬號後，它會送 ...
  • 第28篇 如何.net中實現高效可靠數據同步api
    通過以下方式可以高效，並保證數據同步的可靠性 1.API設計 使用RESTful設計，確保API端點明確，並使用適當的HTTP方法（如POST用於創建，PUT用於更新）。 設計清晰的請求和響應模型，以確保客戶端能夠理解預期格式。 2.數據驗證 在伺服器端進行嚴格的數據驗證，確保接收到的數據符合預期格 ...
所有分類