N皇後 難度分類 困難 題目描述 n皇後問題研究的是如何將 n個皇後放置在 n×n 的棋盤上,並且使皇後彼此之間不能相互攻擊。 上圖為 8 皇後問題的一種解法。 給定一個整數 n,返回所有不同的 n 皇後問題的解決方案。 每一種解法包含一個明確的 n 皇後問題的棋子放置方案,該方案中 'Q' 和 ' ...
N皇後
難度分類
困難
題目描述
n皇後問題研究的是如何將 n個皇後放置在 n×n 的棋盤上,並且使皇後彼此之間不能相互攻擊。
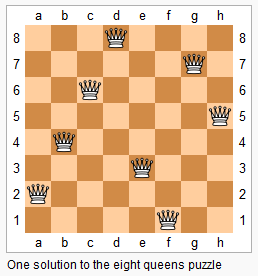
上圖為 8 皇後問題的一種解法。
給定一個整數 n,返回所有不同的 n 皇後問題的解決方案。
每一種解法包含一個明確的 n 皇後問題的棋子放置方案,該方案中 'Q' 和 '.' 分別代表了皇後和空位。
示例:
輸入: 4
輸出: [
[".Q..", // 解法 1
"...Q",
"Q...",
"..Q."],
["..Q.", // 解法 2
"Q...",
"...Q",
".Q.."]
]
演算法圖示
Step1:遍歷第一行所有的列,先在第一行的第一個位置放置第一個皇後,第一個皇後放置後其對應的位置以及衝突位置如下:

Step2:遍歷第二行所有的列,發現第一第二列衝突,第三列個可以放第二個皇後,放置後如圖,放置後對應的位置以及衝突位置如下:
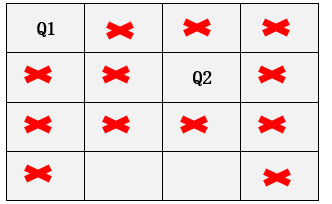
Step3: 遍歷第三行所有的列,發現沒有位置放置第三個皇後,所有列均衝突,所有此種情況下第三行無法放置第三個皇後(不可能得到最終解)。因此回到第二行,繼續遍歷第二行的第四列查看是否可以放置第二個皇後,放置後對應位置以及衝突位置如下:

Step4: 在調整了第二個皇後的位置後繼續遍歷第三行所有的列,發現第二列可以放置第三個皇後,放置後對應位置以及衝突位置如下:Step3: 遍歷第三行所有的列,發現沒有位置放置第三個皇後,所有列均衝突,所有此種情況下第三行無法放置第三個皇後(不可能得到最終解)。因此回到第二行,繼續遍歷第二行的第四列查看是否可以放置第二個皇後,放置後對應位置以及衝突位置如下:

Step5: 遍歷第四行所有的列,發現沒有位置放置第三個皇後,所有列均衝突,此時回到第三步,遍歷第三行的第三四列查看是否可以放置第三個皇後,發現均衝突的情況下回到第二行發現第二行的皇後也無法調整位置了回到第一行,將第一行的皇後放在第二列,繼續求解放置後對應位置以及衝突位置如下:
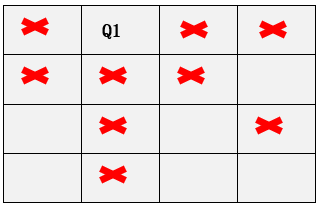
Step6: 在第一行第二列的基礎上查看第二行/第三行/第四行依次這樣每行的查找,當檢查完第一行所有的列後嘗試完所有的結果。
演算法
根據上面的圖示,這種搜索嘗試過程中尋找問題的解,但當探索到某一步時,發現原先選擇並不優或達不到目標,就退回一步重新選擇。這種解題方法我們可以很容易想到使用回溯演算法來解此題,將其轉換為演算法的步驟如下:
演算法第一步
找出約束函數用於去除不合法的解,如圖示中已經在第一行第一列的位置放置了皇後的情況下,如果查找放置第二個皇後的約束條件。這裡的約束條件如下:
|
01 |
02 |
03 |
04 |
|
11 |
12 |
13 |
14 |
|
21 |
22 |
23 |
24 |
|
31 |
32 |
33 |
34 |
- 判斷每次輸入的皇後是否在同一行同一列
- 判斷每次輸入的皇後與以前的皇後是否在同一 ‘/’ 斜線上的位置,此種情況下橫縱坐標之和相同
- 判斷每次輸入的皇後與以前的皇後是否在同一 ‘\’ 斜線上的位置,此種情況下橫縱坐標之差相同
轉換為偽代碼,假定設置2個變數,一個place_queens存放已放置皇後的位置的縱坐標,一個new_queen記錄新來的皇後的位置的縱坐標:
- place_queens裡面的格式為[x1,x2,x3…],每個x值本身表示其所在的列的索引,每個x本身在place_queens裡面的索引表示其所在的行。比如[1,3,0]表示第一行放在第二列,第二行放在第四列,第三行放在第1列,
- 根據a步驟得知len(place_queens)-1表示已放置皇後的最後一行的行號,因此len(place_queens)表示新來的皇後的行號,new_queen的值表示列號
- 如果new_queen與現有place_queens裡面的值相等,則證明新皇後與以前的某一個皇後被放到同一列了,因此返回衝突True
- 如果新皇後的行號-新皇後的列號 = 某一已放置皇後的行號-某一已放置皇後的列號即len(placed_queens)-new_queen == pos - placed_queens[pos]則證明新皇後與以前的某一個皇後在同一“\”,因此返回衝突True
- 如果新皇後的行號+新皇後的列號 = 某一已放置皇後的行號+某一已放置皇後的列號即len(placed_queens)+new_queen == pos + placed_queens[pos]則證明新皇後與以前的某一個皇後在同一“/”,因此返回衝突True
- 其他情況不衝突,返回False
演算法第二步
實現主函數,根據演算法圖示我們可以知道八皇後的主要實現就是遍歷每一行的每一列,如果能放置皇後,則查看接下來的一行,如果不能放置皇後遍歷下一列,這樣遍歷完所有行的所有列,則可得出N皇後的所有解。得出主體函數就做了2件事:
- 從第一行開始遍歷該行的每一列,如果能放置皇後(不衝突),處理下一行,如果不能放置皇後(衝突),繼續遍歷該行的下一列
- 當處理到最後一行的時候,仍然遍歷最後一行的所有列,如果能放置皇後,則找到了一個解,將此解放入結果列表中
演算法第三步
我們已經得到了八皇後的解,將其轉換為如下格式:
[
[".Q..", // 解法 1
"...Q",
"Q...",
"..Q."],
["..Q.", // 解法 2
"Q...",
"...Q",
".Q.."]
]
根據前面的演算法我們得出N皇後的解的格式如[[1, 3, 0, 2], [2, 0, 3, 1]],映射到題目需要的解,則將[[1, 3, 0, 2], [2, 0, 3, 1]]轉換為需要的格式即可具體轉換過程為:
- 遍歷前聲明一個解的列表ans=[]
- 遍歷解的每一行,聲明每一行的解格式each_row = ['.']*n,
- 然後修改對應位置為Q,修改方式為each_row[row] =’Q’
- 修改後將each_row轉換為字元串插入ans中
- 遍歷結束後將ans插入result中
- 回溯剪枝
- 列表和字元串轉換
考點
回溯
代碼
def conflict(placed_queens,new_queen): '''約束函數,用於檢查新來的皇後(new_queen)是否和已放置的皇後(placed_queens)是否會互相攻擊,如果會返回True,否則返回False''' if new_queen in placed_queens:#如果新的皇後和之前的皇後放置在同一列,縱坐標相等 return True for pos in range(len(placed_queens)):#place_queens裡面存儲皇後的格式為place_queens[橫坐標]=縱坐標 if len(placed_queens)-new_queen == pos - placed_queens[pos]:#在同一 ‘\’ 斜線上的位置,橫縱坐標之差相等 return True if len(placed_queens)+new_queen == pos + placed_queens[pos]:#同一 ‘/’ 斜線上的位置,橫縱坐標之和相等 return True return False def dfs(n, place_queens=[],result=[]): if len(place_queens) == n - 1:#如果是放置最後一個皇後,即最後一行檢查 for i in range(n):#遍歷所有的列 if not conflict(place_queens, i):#如果不衝突,放置皇後 place_queens+=[i]# place_queens+=[i]為一個解 #將解轉換為目標格式 ans = [] for pos in place_queens: each_row = ['.']*n each_row[pos] ='Q' ans.append(''.join(each_row)) result.append(ans) for i in range(n):#遍歷每行所有的列 if not conflict(place_queens, i):#如果不衝突,放置皇後 dfs(n, place_queens + [i],result)#檢查下一行可放置皇後位置,place_queens + [i]表示記錄當前不衝突的皇後值,放入place_queens中 return result print(dfs(5)
附加代碼-N皇後執行步驟輔助理解代碼
def confict(place_queens, new_queen): '''place_queens:已放皇後的位置;new_queen:當前要放的皇後的位置''' nextY = len(place_queens) if new_queen in place_queens:#如果要放的位置已經放過了,則肯定衝突 return True '''判斷斜線''' for i in range(nextY): #print(len(state), pos, i, state[i]) if nextY-new_queen == i-place_queens[i]: return True#是否在同一 ‘\’ 斜線上,如果要放的位置與現有皇後的位置處於正斜線上則衝突 if nextY+new_queen == i+place_queens[i]: return True#是否在同一 ‘/’ 斜線上,如果要放的位置與現有皇後的位置處於反斜線上則衝突 return False def queens(num, place_queens=(),steps = 1): '''num:皇後的個數,place_queens:已放皇後的位置''' #查看放置皇後位置,Q表示皇後,x表示非皇後 print('當前檢查第%s行,已放置皇後的位置:%s'%(steps,place_queens)) if len(place_queens)==num-1:#如果前面已經放了num-1個位置了,當前即為最後一步,此時找到不衝突的位置,返回這個位置 for column in range(num): if not confict(place_queens, column): print('-'*100) print('通知:找到了最後一行的皇後放置位置啦,現告知第%s行!!!'%(steps -1)) print((column,)) yield (column,) else:#如果當前不是最後一步 for column in range(num):#遍歷當前行所有的位置 if not confict(place_queens, column):#如果在當前行當前位置上放置皇後不衝突 for result in queens(num, place_queens+(column,),steps+1):#就在當前位置上放置皇後,記錄place_queens if steps!=1: print('通知:我們是第%s行,我們已收到通知第%s行的皇後找到了啦,現告知第%s行!!!' % (steps,steps+1,steps-1)) print((column,) + result) else: print('通知:我們已經收到下層反饋,找到了一個解!!!') print((column,) + result) print('-' * 100) yield (column,) + result result = [] num = 4 for each_ans in queens(num): result.append(each_ans) print() print('最終解:',result) print('轉換為皇後位置排列如下:') print('-'*100) for each_ans in result: for column in each_ans: temp = ['.'] * num temp[column] = 'Q' print(temp) print('-'*100)



