1.knnK最近鄰(k-Nearest Neighbor,KNN)分類演算法,在給定一個已經做好分類的數據集之後,k近鄰可以學習其中的分類信息,並可以自動地給未來沒有分類的數據分好類。我們可以把用戶分為兩類:“高信譽用戶”和“低信譽用戶”,酒店則可以分為:“五星”,“四星”,“三星”,“兩星”,“一星 ...
1.knn
K最近鄰(k-Nearest Neighbor,KNN)分類演算法,在給定一個已經做好分類的數據集之後,k近鄰可以學習其中的分類信息,並可以自動地給未來沒有分類的數據分好類。
我們可以把用戶分為兩類:“高信譽用戶”和“低信譽用戶”,酒店則可以分為:“五星”,“四星”,“三星”,“兩星”,“一星”。
這些可以使用線性回歸做分類嗎?
答案:能做,但不建議使用,線性模型的輸出值是連續性的實數值,而分類模型的任務要求是得到分類型的模型輸出結果。從這一點上看,線性模型不適合用於分類問題。
我們換一個思路,這裡用“閾值”概念,也就是將連續性數值離散化,比如信譽預測中,我們可以把閾值定為700,高於700的為高信譽用戶,低於700的為低信譽用戶,這裡我們把連續性變數轉換成一個“二元變數”,當然也可以使用更多“閾值”,比如可以分為,低信譽,中等信譽,高信譽。
###############################################################
回歸與分類的不同
1.回歸問題的應用場景(預測的結果是連續的,例如預測明天的溫度,23,24,25度)
回歸問題通常是用來預測一個值,如預測房價、未來的天氣情況等等,例如一個產品的實際價格為500元,通過回歸分析預測值為499元,我們認為這是一個比較好的回歸分析。一個比較常見的回歸演算法是線性回歸演算法(LR)。另外,回歸分析用在神經網路上,其最上層是不需要加上softmax函數的,而是直接對前一層累加即可。回歸是對真實值的一種逼近預測。
2.分類問題的應用場景(預測的結果是離散的,例如預測明天天氣-陰,晴,雨)
分類問題是用於將事物打上一個標簽,通常結果為離散值。例如判斷一幅圖片上的動物是一隻貓還是一隻狗,分類通常是建立在回歸之上,分類的最後一層通常要使用softmax函數進行判斷其所屬類別。分類並沒有逼近的概念,最終正確結果只有一個,錯誤的就是錯誤的,不會有相近的概念。最常見的分類方法是邏輯回歸,或者叫邏輯分類。
############################################################
如下圖所示,我們想要知道綠色點要被決定賦予哪個類,是紅色三角形還是藍色正方形?我們利用KNN思想,如果假設K=3,選取三個距離最近的類別點,由於紅色三角形所占比例為2/3,因此綠色點被賦予紅色三角形類別。如果假設K=5,由於藍色正方形所占比例為3/5,因此綠色點被賦予藍色正方形類別。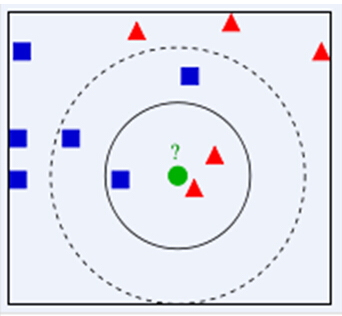
從上面實例,我們可以總結下KNN演算法過程
1.1. 計算測試數據與各個訓練數據之間的距離。
1.2. 按照距離的遞增關係進行排序,選取距離最小的K個點。
1.3. 確定前K個點所在類別的出現頻率,返回前K個點中出現頻率最高的類別作為測試數據的預測分類。
從KNN演算法流程中,我們也能夠看出KNN演算法三個重要特征,即距離度量方式、K值的選取和分類決策規則。
1.1距離:
KNN演算法常用歐式距離度量方式,當然我們也可以採用其他距離度量方式,如曼哈頓距離
歐氏距離是最容易直觀理解的距離度量方法,兩個點在空間中的距離一般都是指歐氏距離。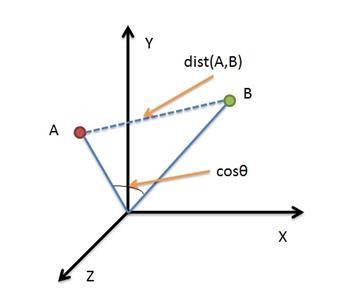
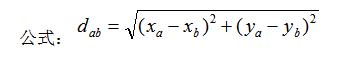
1.2 K值的選取: KNN演算法決策結果很大程度上取決於K值的選擇。選擇較小的K值相當於用較小領域中的訓練實例進行預測,訓練誤差會減小,但同時整體模型變得複雜,容易過擬合。選擇較大的K值相當於用較大領域中訓練實例進行預測,可以減小泛化誤差,但同時整體模型變得簡單,預測誤差會增大。
1.3 分類決策規則:k值中對象們“投票”,哪類對象“投票”數多就屬於哪類,如果“投票”數一樣多,那麼隨機抽選出一個類。
2.1knn KD樹
我們舉例來說明KD樹構建過程,假如有二維樣本6個,分別為{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)},KD樹過程構建過程如下
2.1.1尋找劃分特征: 6個數據點在x,y維度上方差分別為6.97,5.37,x軸上方差更大,用x軸特征建樹。
######################################################

方差或表達為:
######################################################
2.1.2Node-data = (7,2)。具體是:根據x維上的值將數據排序,6個數據的中值(所謂 中值,即中間大小的值)為7,所以Node-data域位數據點(7,2)。這樣,該節點的分割超平面就是通過(7,2)並垂直於:split=x軸的直線x=7
2.1.3左子空間和右子空間。具體是:分割超平面x=7將整個空間分為兩部分:x<=7的部分為左子空間,包含3個節點={(2,3),(5,4),(4,7)};另一部分為右子空間,包含2個節點={(9,6),(8,1)};
2.1.4遞歸構建KD樹:用同樣的方法劃分左子樹{(2,3),(5,4),(4,7)}和右子樹{(9,6),(8,1)},最終得到KD樹。
如左子樹{(2,3),(5,4),(4,7)} x軸方差 2.3,y軸方差4.3,所有使用y軸進行分割
重覆上面2.1,2.2,2.3 步驟 ,中值為5.4

首先,粗黑線將空間一分為二,然後在兩個子空間中,細黑直線又將整個空間劃分為四部分,最後虛黑直線將這四部分進一步劃分。
2.2 KD樹搜索最近鄰
當我們生成KD樹後,就可以預測測試樣本集裡面的樣本目標點。
1 二叉搜索:對於目標點,通過二叉搜索,能夠很快在KD樹裡面找到包含目標點的葉子節點。
2回溯:為找到最近鄰,還需要進行回溯操作,演算法沿搜索路徑反向查找是否有距離查詢點更近的數據點。以目標點為圓心,目標點到葉子節點的距離為半徑,得到一個超球體,最鄰近點一定在這個超球體內部。
3更新最近鄰:返回葉子節點的父節點,檢查另一葉子節點包含的超矩形體是否和超球體相交,如果相交就到這個子節點中尋找是否有更近的最近鄰,有的話就更新最近鄰。如果不相交就直接返回父節點的父節點,在另一子樹繼續搜索最近鄰。當回溯到根節點時,演算法結束,此時保存的最近鄰節點就是最終的最近鄰。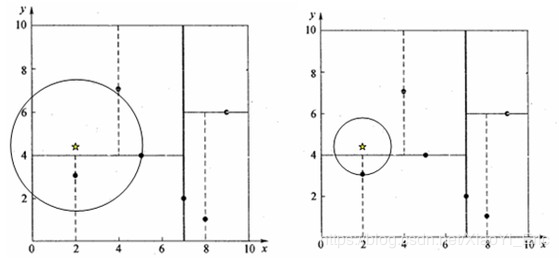
2.3KD樹預測
根據KD樹搜索最近鄰的方法,我們能夠得到第一個最近鄰數據點,然後把它置為已選。然後忽略置為已選的樣本,重新選擇最近鄰,這樣運行K次,就能得到K個最近鄰。如果是KNN分類,根據多數表決法,預測結果為K個最近鄰類別中有最多類別數的類別。如果是KNN回歸,根據平均法,預測結果為K個最近鄰樣本輸出的平均值。



