1.線性回歸模型線性回歸是統計學中最常用的演算法,當你想表示兩個變數間的數學關係時,就可以用線性回歸。當你使用它時,你首先假設輸出變數(相應變數、因變數、標簽)和預測變數(自變數、解釋變數、特征)之間存在的線性關係。(自變數是指:研究者主動操縱,而引起因變數發生變化的因素或條件,因此自變數被看作是因變 ...
1.線性回歸模型
線性回歸是統計學中最常用的演算法,當你想表示兩個變數間的數學關係時,就可以用線性回歸。當你使用它時,你首先假設輸出變數(相應變數、因變數、標簽)和預測變數(自變數、解釋變數、特征)之間存在的線性關係。
(自變數是指:研究者主動操縱,而引起因變數發生變化的因素或條件,因此自變數被看作是因變數的原因。
因變數是指:在函數關係式中,某個量會隨一個(或幾個)變動的量的變動而變動。)
線性模型可能使用於類似下麵的問題:比如你正在研究一個公司的銷售額和該公司在廣告上的投入之間的關係,或者某人在社交網站上的好友數量和他每天在該社交網站上花費的時間之間的關係。
理解線性回歸一個切入點是先確定那條直線,我們知道,通過斜率和截距就可以完全確定一條直線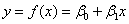
例子1:
假設 (用戶數,利潤值)
S={(x,y)=(1,25),(10,250),(100,2500)}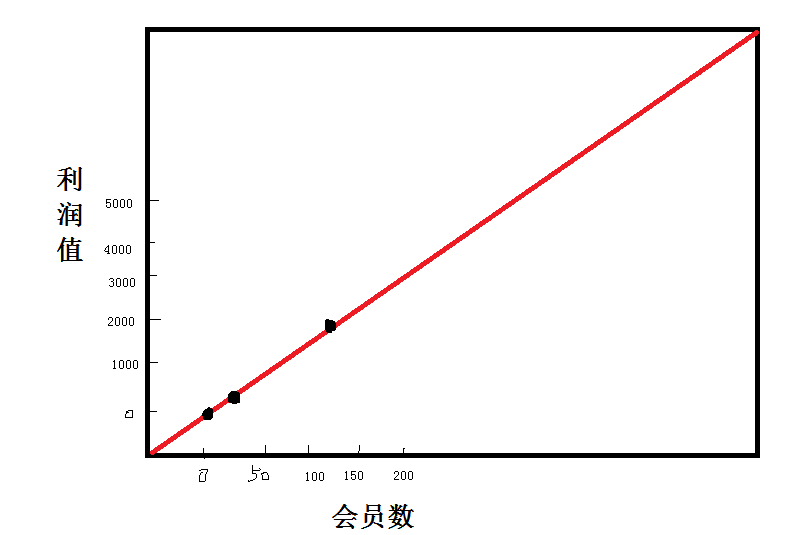
例子2:
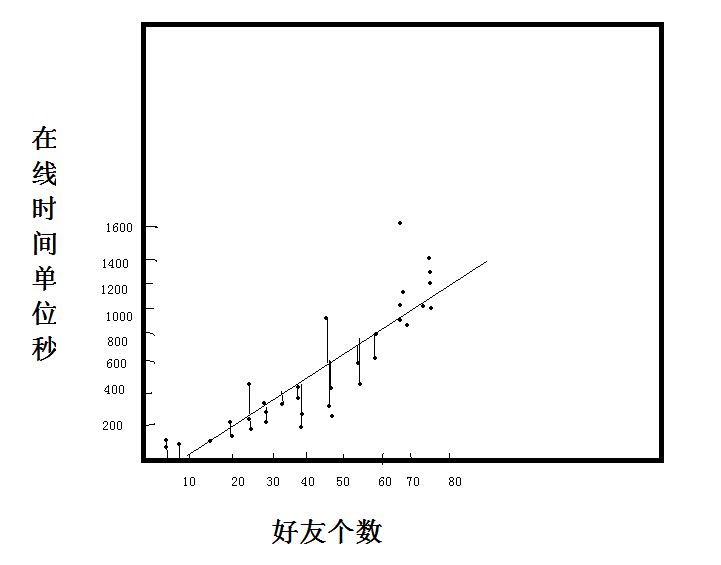
假設(好友數,線上時間)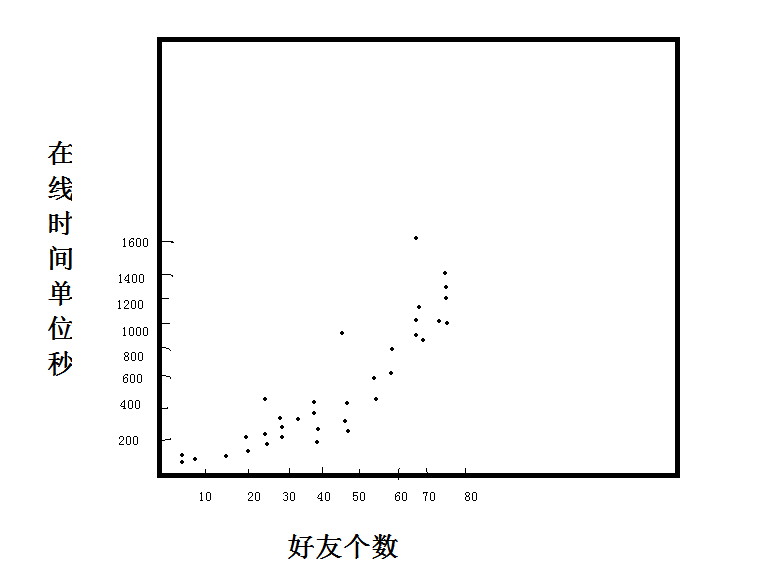
看到當前圖片,很難一眼看出兩個變數之間的關係了。
我們假設圖中是線性關係,可以畫出多條線。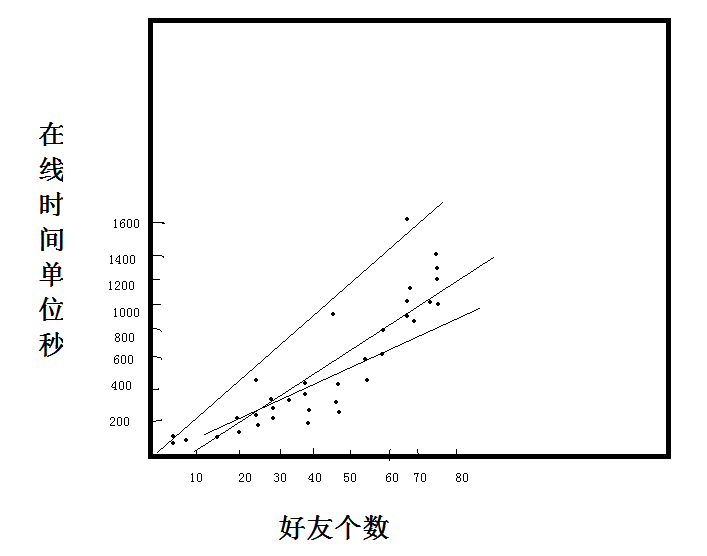
那麼哪條線才是我們使用的最優線呢?這是一個擬合過程
2.spark ALS
ALS中文名作交替最小二乘法,就是在最小二乘法基礎上的升級,在機器學習中,ALS特指使用最小二乘法求解的一個協同過濾演算法,是協同過濾中的一種。ALS演算法是2008年以來,用的比較多的協同過濾演算法。從協同過濾的分類來說,ALS演算法屬於User-Item CF,也叫做混合CF,因為它同時考慮了User和Item兩個方面,即即可基於用戶進行推薦又可基於物品
如下圖所示,u表示用戶,v表示商品,用戶給商品打分,但是並不是每一個用戶都會給每一種商品打分。比如用戶u6就沒有給商品v3打分,需要我們推斷出來,這就是機器學習的任務。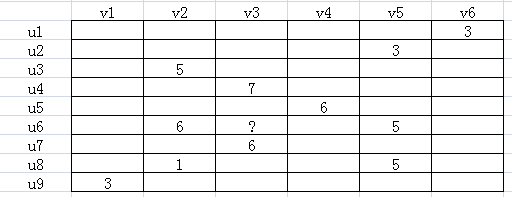
由於並不是每個用戶給每種商品都打了分,可以假設ALS矩陣是低秩的,即一個m*n的矩陣,是由m*k和k*n兩個矩陣相乘得到的,其中k<<m,n。
Am×n=Um×k×Vk×n
這種假設是合理的,因為用戶和商品都包含了一些低維度的隱藏特征,比如我們只要知道某個人喜歡碳酸飲料,就可以推斷出他喜歡百世可樂、可口可樂、芬達,而不需要明確指出他喜歡這三種飲料。這裡的碳酸飲料就相當於一個隱藏特征。上面的公式中,Um×k表示用戶對隱藏特征的偏好,Vk×n表示產品包含隱藏特征的程度。機器學習的任務就是求出Um×k和Vk×n。可知uiTvj是用戶i對商品j的偏好,使用Frobenius範數來量化重構U和V產生的誤差。由於矩陣中很多地方都是空白的,即用戶沒有對商品打分,對於這種情況我們就不用計算未知元了,只計算觀察到的(用戶,商品)集合R。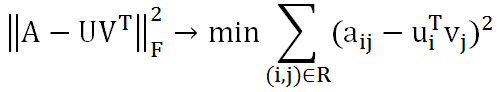
這樣就將協同推薦問題轉換成了一個優化問題。目標函數中U和V相互耦合,這就需要使用交替二乘演算法。即先假設U的初始值U(0),這樣就將問題轉化成了一個最小二乘問題,可以根據U(0)可以計算出V(0),再根據V(0)計算出U(1),這樣迭代下去,直到迭代了一定的次數,或者收斂為止。雖然不能保證收斂的全局最優解,但是影響不大。



