OO第一單元作業總結

　　在第一單元作業中，我們只做了一件事情：求導，對多項式求導，對帶三角函數的表達式求導，對有括弧嵌套的表達式求導。作業難度依次遞增，讓我們熟悉面向對象編程方法，開始從面向過程向面向對象轉變。本文中，我將介紹我個人每一次作業的做法，以及三次作業的分析，互測時策略。

第一次作業

　　第一次作業由於只對多項式進行求導，求導的函數只有冪函數，項與項之間僅有和關係，因此處理起來比較簡單，輸入可以使用正則表達式提取數據，存儲可以使用HashMap，這樣可以很方便的實現合併同類項，輸出也只需要判斷幾種省略條件。

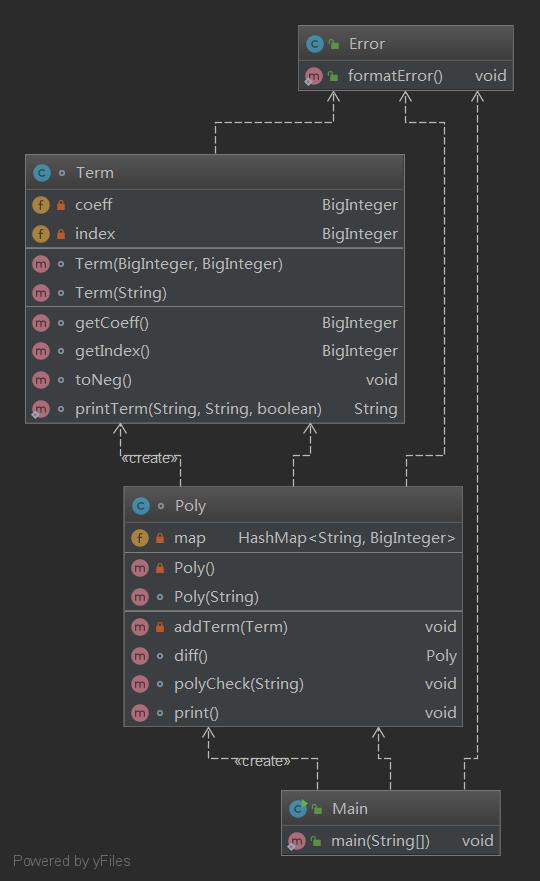
　　結構上，我定義了一個Poly類和Term類分別來處理多項式和項。每個項有自己的指數和繫數，一個多項式由項與項之間的和關係構成。多項式求導時，每個項求導後還是一項，求導後的項又可以構成一個新的多項式。輸出時，多項式的輸出是每個項輸出的結合。整體結構非常簡單，直觀。

第二次作業

　　第二次作業中出現了sin(x), cos(x)因數，而且出現了乘積關係（常數因數、冪函數因數、三角函數因數），情況比第一作業複雜。但是常數因數可以合併為繫數，冪函數因數也可以合併，兩種三角函數因數也可以合併，因此我們可以得到每一項又一個四元組組成（繫數，冪函數指數，sin(x)指數，cos(x)指數）。同樣適用上一次HashMap的方法，將三種指數變成類似“x1s2c3”，這樣的String字元串，就可以作為HashMap的key，繫數作為HashMap的value，這樣就可以實現合併同類項了。求導時，根據求導公式，每個項求導會得到三個新的項，也可以用四元組表示。因此第二次作業與第一次作業結構上類似。

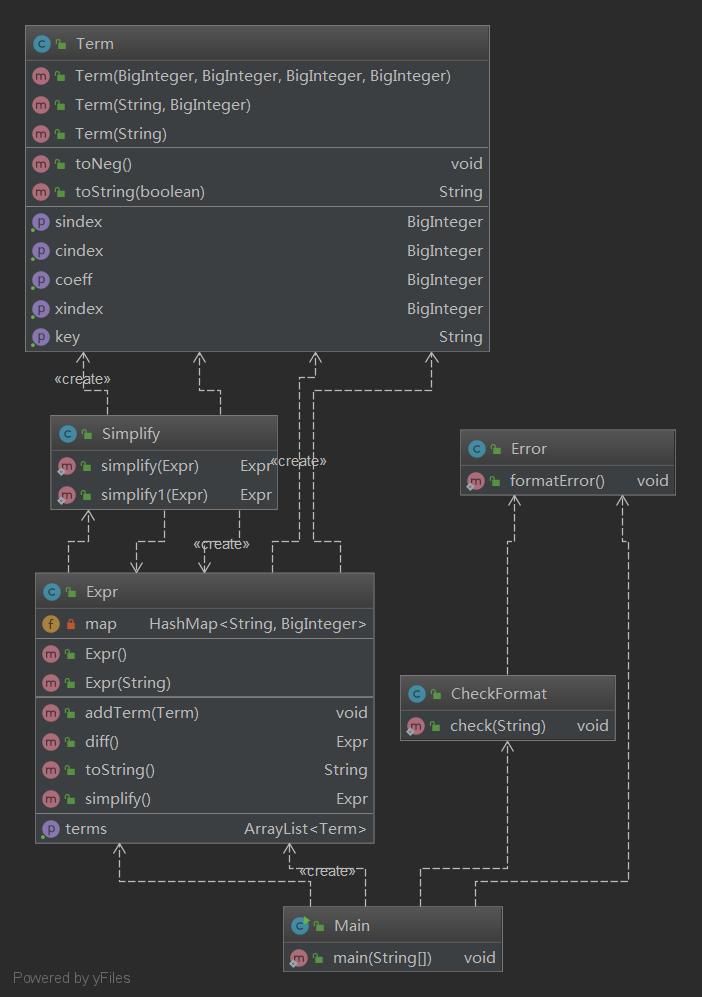
　　第二次作業比較麻煩的地方在於化簡表達式的長度，比較基本的化簡方法有：sin(x)^2 + cos(x)^2 = 1, 1 - sin(x)^2 = cos(x)^2, 1 - cos(x)^2 = sin(x)^2。依次枚舉每個項，按照上述方法進行化簡。這樣的做法雖然的到的不是最簡的，但是對於基本的表達式有著不錯的化簡效果。由於項與項之間的結合順序不同，可能得到不同的化簡結果，這樣可能陷入局部級值，因此加入隨機化改變排列順序，則會得到更好的結果。（來自hdl的做法）。

第三次作業

　　第三次作業中出現了括弧，多出了表達式因數( (E), E為表達式 )，和嵌套因數( sin(F), cos(F), F為一個因數 )。因此整個結構會變得很複雜，多了很多嵌套的情況。一個表達式為項與項之間的和，一個項為因數之間的乘積。在存儲時，使用ArrayList，表達式存表達式內的每一項，項存項內的每個因數。每種因數之間有相同的方法（求導，輸出等），每種因數又不相同，因此構建一個因數的抽象類實現共性方法，再用不同的子類實現個性方法。這樣，項在處理因數的時候，就可以使用同一的介面進行調用。

　　輸入處理時，不能直接使用正則表達式處理括弧嵌套的情況。我的做法是，先將提取表達式串中的最大子表達式串（子表達式外只有一層括弧，多層括弧取最外層括弧內部為子表達式，同時嵌套因數內部也判斷為子表達式），然後用字母E代替子表達式。這樣一個表達式串內就沒有括弧嵌套的情況，可以使用正則表達式處理。對於子表達式串，先建立表達式對象，然後存在一個ArrayList里，在之後建立表達式因數和嵌套因數時，從ArrayList里取出，存到相應的因數里。這樣即可完成相應的因數構建。

　　求導時，每個因數可以單獨求導返回一個因數集合，對去嵌套因數，表達式因數，內部可以直接調用表達式求導的方法，得到一個新的因數。每個項求導，根據求導公式，可以得到一個項的集合，每一項都是一個因數求導和其他因數拼接。表達式求導，得到一個表達式。層次非常清晰。

　　輸出時，表達式輸出為內部項輸出的拼接，項輸出為內部因數輸出的拼接，每一個因數返回一個串，嵌套因數，表達式因數調用內部表達式的輸出。輸出邏輯也很清晰。

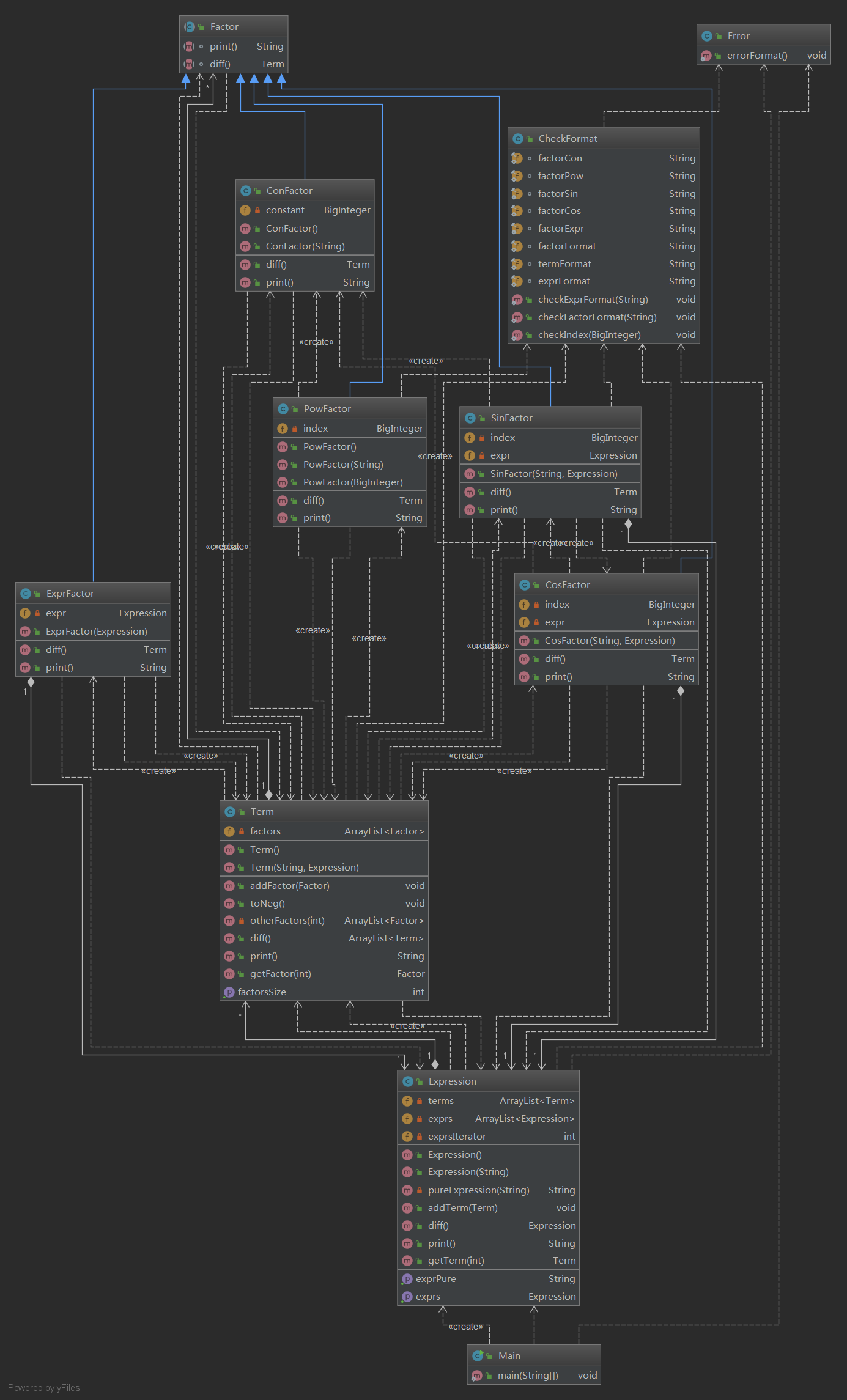
到目前為止，第三次作業的架構都非常清晰。

第三次作業化簡方法

　　不要做化簡，不要做化簡，不要做化簡！

　　如果做了化簡，就會變成這樣：

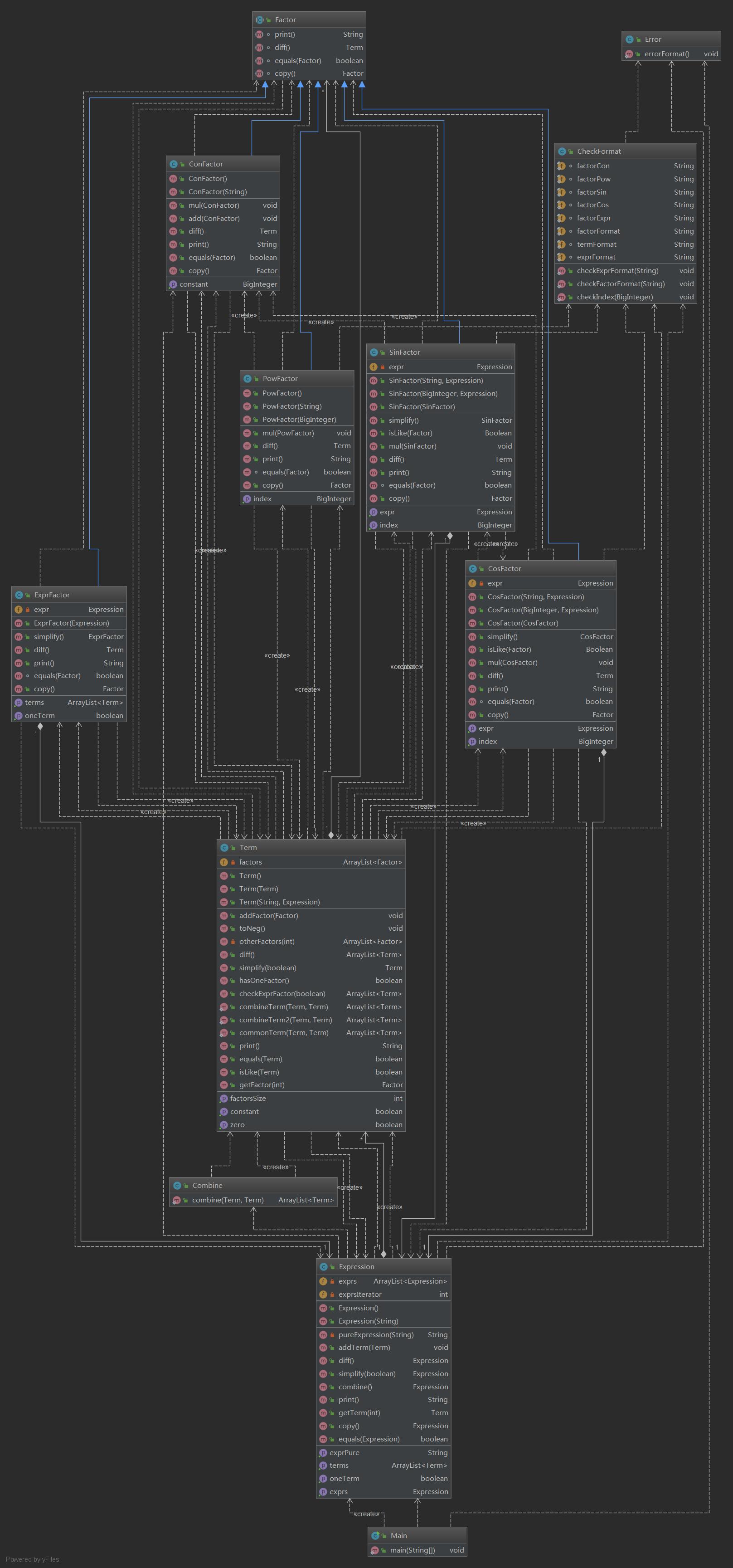
　　基於之前第三次作業的架構，我設計了一套化簡方法，但是由於代碼能力的不足，和思考時的斷層，代碼實現上出現了較大問題，需要重構。

　　首先我們要考慮化簡需要做什麼，去括弧，去掉多於的項，去掉多於的因數，合併相同的因數，項與項之間的合併等等。但是仔細一想，這些化簡中都需要判斷表達式是否相等。而表達式相等的判斷，只有化簡後才能進行。這個邏輯很奇怪，但是仔細一想，化簡的時候，需要判斷的是內部表達式是否相等，那麼在化簡這一層表達式的時候，先化簡下一層表達式就可以進行相等判斷了。

　　相等判斷的做法是，因數可以直接判斷是否相等。對於兩個項之間，需要判斷一項中的所有因數是否在另一項中存在，這裡可以使用一個標記數組來實習判斷。表達式之間操作與項之間類似。

化簡步驟：

• 化簡內部表達式（因數）
• 去掉多餘表達式因數（去括弧）（項）
• 合併相同的因數（項）
• 去掉多餘的因數（項）
• 去掉多餘的項（表達式）
• 項之間提取公因數（表達式）
• 項與項之間合併（表達式）

　　在這個化簡步驟里有一個令人興奮的現象：這些化簡步驟是自底向上的，這樣讓我們實現遞歸成為可能。接下來我們分步陳述。

　　化簡內部表達式。調用表達式化簡方法就好。

　　去掉多表達式因數（去括弧）。去括弧的意義在於，可以方便後邊的合併。能去括弧的情況有二種。一是括弧內只有一項（因數的積），那麼我們可以把所有因數提取出來與外邊的因數相乘。二是括弧外無其他因數（繫數為1），則將括弧內的每一項提出來。

　　合併相同的因數。繫數相乘，底數相同指數相加，表達式因數不合併。這裡需要用到表達式相等的判斷。

　　去掉多餘的因數。項中，指數為0的因數可以剔除，不剔除會對相等判斷造成影響。

　　去掉多餘的項。表達式中，繫數為0的項可以剔除，不剔除會對相等判斷造成影響。

　　提取公因數。枚舉兩項，將相同的因數提取出來，其他因數建立成一個表達式因數（加括弧）。

　　項與項之間合併。枚舉兩項，如果同為常數項，則相加，如果滿足三角函數合併條件則合併。

　　以上是我本人的合併思路，效果還好，可能由於個人實現出了問題，導致有些情況效果沒有達到完美。

代碼分析

第一次作業

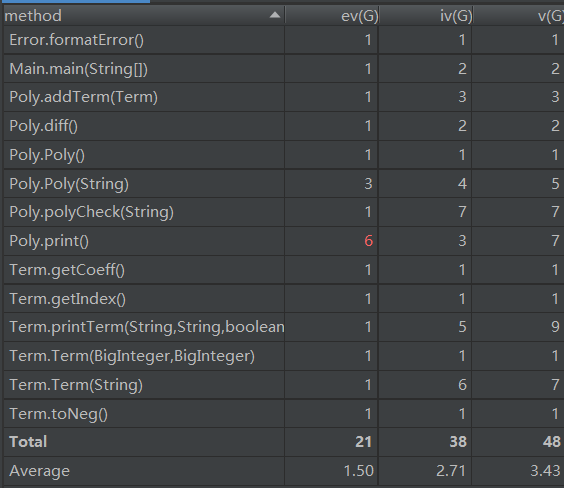
　　第一次代碼整體結構非常簡單，只有在輸出判斷的時候有很多分支判斷。

第二次作業

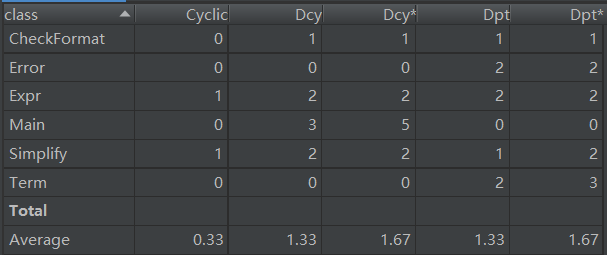
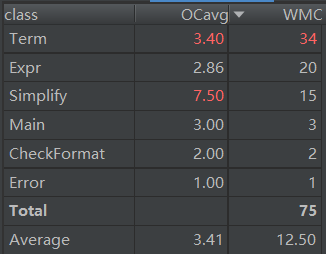
第三次作業

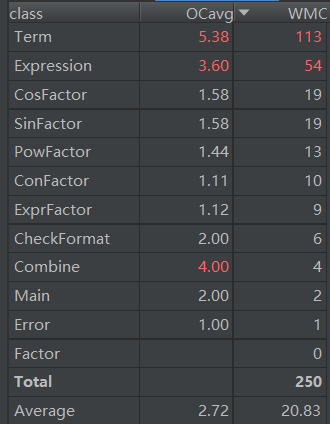
　　第二次作業和第三次作業出現的問題類似，都是把過多的操作交給一個類去完成。在第二次這個影響還不明顯，但是到第三次由於化簡需要大量代碼來實現，導致類內部很臃腫（Term類超出了500行）。這個原因是我對面向對象認識不夠，只是機械的把具體的事物設置成為一個類，沒有認識到對事物的操作也可以為一個類。

互測攻防戰

第一次作業

　　敵方：由於是第一次，有些同學由於審題不認真，導致了輸入格式處理出現了bug。有些同學在輸出上判斷出了bug。而在求導部分出現bug的人很少。

　　我方：在一次次萬箭齊發中，存活。

第二次作業

　　敵方：有一位同學對於輸出為0的情況處理不到位，導致沒出輸出。

　　我方：在一次次南蠻入侵中，存活。

第三次作業

　　敵方：有一位同學在輸入處理的時候正則表達式出了問題，導致了bug。

　　我方：在一次次槍林彈雨中，存活。

反思

　　本單元的三次作業，讓我一步步從接觸面向對象到熟練使用面向對象的思想，最終構建起來可以拓展的框架。但是由於繼承多態那裡使用不熟練，導致很多代碼沒有使用到多態的特性，用了大段判斷語句。而且我對設計模式也不夠瞭解，設計思路比較原始，今後需要進步。