今天佛了,魔鬼周一,線上教學,有點小累,但還好,今天AC了一道,每日一道,還好達成目標,還以為今天完不成了,最近任務越來越多,如何高效完成該好好思考一下了~最重要的還是學業的複習和預習。 今日興趣新聞: 《流浪地球》中的逃生氣囊球和馬斯克有什麼關係? 鏈接:https://mbd.baidu.com ...
今天佛了,魔鬼周一,線上教學,有點小累,但還好,今天AC了一道,每日一道,還好達成目標,還以為今天完不成了,最近任務越來越多,如何高效完成該好好思考一下了~最重要的還是學業的複習和預習。
今日興趣新聞:
《流浪地球》中的逃生氣囊球和馬斯克有什麼關係?
鏈接:https://mbd.baidu.com/newspage/data/landingsuper?context=%7B%22nid%22%3A%22news_8599496962815210358%22%7D&n_type=0&p_from=1
------------------------------------------------題目----------------------------------------------------------
Polycarp and Div 3
Polycarp likes numbers that are divisible by 3.
He has a huge number ss. Polycarp wants to cut from it the maximum number of numbers that are divisible by 33. To do this, he makes an arbitrary number of vertical cuts between pairs of adjacent digits. As a result, after mm such cuts, there will be m+1m+1 parts in total. Polycarp analyzes each of the obtained numbers and finds the number of those that are divisible by 33.
For example, if the original number is s=3121s=3121, then Polycarp can cut it into three parts with two cuts: 3|1|213|1|21. As a result, he will get two numbers that are divisible by 33.
Polycarp can make an arbitrary number of vertical cuts, where each cut is made between a pair of adjacent digits. The resulting numbers cannot contain extra leading zeroes (that is, the number can begin with 0 if and only if this number is exactly one character '0'). For example, 007, 01 and 00099 are not valid numbers, but 90, 0 and 10001 are valid.
What is the maximum number of numbers divisible by 33 that Polycarp can obtain?
Input
The first line of the input contains a positive integer ss. The number of digits of the number ss is between 11 and 2⋅1052⋅105, inclusive. The first (leftmost) digit is not equal to 0.
Output
Print the maximum number of numbers divisible by 33 that Polycarp can get by making vertical cuts in the given number ss.
Examples
input
3121
output
2
input
6
output
1
input
1000000000000000000000000000000000
output
33
input
201920181
output
4
Note
In the first example, an example set of optimal cuts on the number is 3|1|21.
In the second example, you do not need to make any cuts. The specified number 6 forms one number that is divisible by 33.
In the third example, cuts must be made between each pair of digits. As a result, Polycarp gets one digit 1 and 3333 digits 0. Each of the 3333digits 0 forms a number that is divisible by 33.
In the fourth example, an example set of optimal cuts is 2|0|1|9|201|81. The numbers 00, 99, 201201 and 8181 are divisible by 33.
------------------------------------------------題目----------------------------------------------------------
(一) 原題大意:
輸入一個數,某人可以進行以下的操作:
某人可以進行任意數量的垂直切割,其中每個切割在一對相鄰的數字之間進行。結果數字不能包含額外的前導零(也就是說,當且僅當此數字恰好是一個字元' 0 '時,數字才能以0開頭)。例如,007,01和00099不是有效的數字,但90,0和10001是有效的。
分割出來的每一部分的數,都能被3整除,則說明可以得到一個整除3的數,其中0也能被3整除,請算一算能為該同學獲得最多幾個整除3的數呢?
(二) 題目分析:
首先,肯定是需要得到每一個數字,如果這個數字是0,那麼答案比較簡單,如果當前數字能夠直接被3整除(0, 3, 6, 9)的話,那就直接結果加一就好了。
然後如果這兩種情況都不成立,那麼就是兩位數以上的組合了,在這裡我出了點彎路子,剛開始用求和法,然後卻瘋狂到test11就WA了,檢查了很久也沒有找到解決辦法,後來心理課結束後和大佬們交談才發現一些新想法奧秘,那就是符合3整除的數,求餘之後有特殊關係,待會列一下我的彎路給自己提個醒。
然後我換了一種方法,那就是用加和,利用整除3的特性,下麵也列出來了,但還是WA了。
最後我翻看一些博客,發現在我原來寫得基礎上,只要改變if條件的位置就能AC了,總結來說有三種情況:當前數字模3為0、現有的數字之和模3為0(當前正在處理的)、隔了三個數字了一定可以做到模3為0
(三) 錯誤彎路:
第一次直接用long long int 去扔輸入,然後丟OJ結果發現第一次就WA了
#include<stdio.h> #include<math.h> long long int temp,num; int temp_num,counter,ans,k; int main() { ans = 0; scanf("%d",&temp); num = temp; while(num>0) { k = num % 10; if(k == 0) { ans++; counter = temp_num = 0; num = num / 10; continue; } if(k % 3 == 0) { ans++; counter = temp_num = 0; } else { temp_num += k * pow(10,counter); if(temp_num % 3 == 0) { ans++; counter = temp_num = 0; } } num = num / 10; } printf("%d\n",ans); return 0; }
結果是因為scanf這裡用了%d,結果才發現過樣例1000000000000000000000000000的時候錯了,然後就換了一種方法,像這樣大數都只能用char來處理了:
第二步彎路,然後就改了改,扔進去:
#include<stdio.h> #include<math.h> #include<string.h> char input[2000005]; int num; int temp_num,counter,ans,k; int main() { ans = 0; scanf("%s",&input); for(int i = strlen(input) - 1;i>=0;i--) { k = input[i]; if(k == 0) { ans++; counter = temp_num = 0; continue; } if(k % 3 == 0) { ans++; counter = temp_num = 0; } else { temp_num += k * pow(10,counter); if(temp_num % 3 == 0) { ans++; counter = temp_num = 0; } } } printf("%d\n",ans); return 0; }
到這裡樣例就都全過了,代碼思路是:將輸入的值扔進char數組裡,然後獲取到他的長度,從後往前來處理,從判斷當前數是否為0,如果是的話就直接加一,然後判斷當前數能否被3整除,如果可以就也直接加一。都沒有的話,就存到一個temp變數里,然後與後面處理的數求和,然後判斷該求和temp是否能被3整除。結果這裡到test11就WA了,半天沒搞懂,後來和同學討論了半天,結果發現對於122 221這樣的數判斷就出現了問題,後來實在解不了,嫌判斷太亂,都單獨列了出來,結果居然AC了:
#include<stdio.h> #include<math.h> #include<string.h> char input[200005]; long long int temp_num,counter,ans,k; int main() { ans = counter = 0; scanf("%s",&input); for(int i = strlen(input) - 1;i>=0;i--) { k = input[i] - '0'; temp_num += k; counter++; if(counter == 3) { ans++; counter = temp_num = 0; continue; } else if(k % 3 == 0) { ans++; counter = temp_num = 0; continue; } else if(temp_num % 3 == 0) { ans++; counter = temp_num = 0; continue; } } printf("%d\n",ans); return 0; }
結果誤打誤撞發現了一些牛皮的數學思維~ 待會獻上:
(四)AC代碼:
因為代碼比較簡單,依舊不分塊了~
#include<stdio.h> #include<math.h> #include<string.h> char input[200005]; long long int temp_num,counter,ans,k; int main() { ans = counter = 0; scanf("%s",&input); for(int i = strlen(input) - 1;i>=0;i--) { k = input[i] - '0'; temp_num += k; counter++; if(counter == 3 || k % 3 == 0 || temp_num % 3 == 0) { ans++; counter = temp_num = 0; } } printf("%d\n",ans); return 0; }
(五)AC截圖:
(六)解後分析:
分析1 - 能被特殊數整除的特征:
1、能被2整除的數的特征。
如果一個數能被2整除,那麼這個數末尾上的數為偶數,“0”、“2”、“4”、“6”、“8”。
2、能被3整除的數的特征。
如果一個數能被3整除,那麼這個數所有數位上數字的和是3的倍數。例如:225能被3整除,因為2+2+5=9,9是3的倍數,所以225能被3整除。
3、能被4整除的數的特征。
如果一個數的末尾兩位能被4整除,這個數就能被4整除。例如:15692512能不能被4整除呢?因為15692512的末尾兩位12,能被4整除,所以15692512能被4整除。
4、能被5整除的數的特征。
若一個數的末尾是0或5,則這個數能被5整除。
5、能被7整除的數的特征。
方法一:若一個整數的個位數字截去,再從餘下的數中,減去個位數的2倍,如果差是7的倍數,則原數能被7整除。如果差太大或心算不易看出是否是7的倍數,就需要繼續上述「截尾、倍大、相減、驗差」的過程,直到能清楚判斷為止。例如,判斷133是否是7的倍數的過程如下:13-3×2=7,所以133是7的倍數;又例如判斷6139是否7的倍數的過程如下:613-9×2=595 , 59-5×2=49,所以6139是7的倍數,以此類推。
方法二:如果一個多位數的末三位數與末三位以前的數字所組成的數的差,是7的倍數,那麼這個數就能被7整除。例如:280678末三位數是678,末三位以前數字所組成的數是280,679-280=399,399能被7整除,因此280679也能被7整除。
方法三:首位縮小法,減少7的倍數。
例如,判斷452669能不能被7整除,452669-420000=32669,只要32669能被7整除即可。可對32669繼續,32669-28000=4669,4669-4200=469,469-420=49,49當然被7整除所以452669能被7整除。
6、能被8整除的數的特征。
若一個整數的未尾三位數能被8整除,則這個數能被8整除。
7、能被9整除的數的特征。
若一個數的數位上的數字的和能被9整除,則這個整數能被9整除。例如:111111111能不能被9整除呢?因為1+1+1+1+1+1+1+1+1=9,9是9的倍數,所以111111111能被9整除。
8、能被11整除的數的特征。
方法一:若一個整數的奇位數字之和與偶位數字之和(從右往左數)的差能被11整除,則這個數能被11整除。例如,判斷491678能不能被11整除。奇位數字之和8+6+9=23;偶位數字之和7+1+4=12;23-12=11,11能被11整除,所以491678能被11整除。這種方法叫作“奇偶位差法”。
方法二:11的倍數檢驗法也可用上述檢查7的「割尾法」處理!過程唯一不同的是:倍數不是2而是1!例如:判斷491678能不能被11整除,49167-8=49159,4915-9=4906,
490-6=484,48-4=44。44能被11整除,所以得491678能被11整除。
方法三:還可以根據7的方法二判斷。例如:283679的末三位數是679,末三位以前數所組成的數是283,679-283=396,396能被11整除,因此283679就一定能被11整除。
9、能被13整除的數的特征。
方法一:若一個整數的個位數字截去,再從餘下的數中,加上個位數的4倍,如果和是13的倍數,則原數能被13整除。如果和太大或心算不易看出是否13的倍數,就需要繼續上述「截尾、倍大、相加、驗和」的過程,直到能清楚判斷為止。
例如,判斷1284322能不能被13整除。128432+2×4=128440,12844+0×4=12844,
1284+4×4=1300,1300÷13=100。所以1284322能被13整除。
方法二:前面7的方法二,也適用判定13。例如:判定1284322能不能被13整除,128432的末尾三位數是322,末尾以前的數字所組成的數是1284,322-1284=-962。962÷13=74。所以1284322能被13整除。
10、能被17整除的數的特征。
方法一:若一個整數的個位數字截去,再從餘下的數中,減去個位數的5倍,如果差是17的倍數,則原數能被17整除。如果差太大或心算不易看出是否17的倍數,就需要繼續上述「截尾、倍大、相減、驗差」的過程,直到能清楚判斷為止。例如,判斷1675282能不能被17整除,167528-2×5=167518,16751-8×5=16711,1671-1×5=1666,166-6×5=136,
136÷17=8,所以1675282能被17整除。
方法二:若一個整數的末三位與3倍的前面的隔出數的差能被17整除,則這個數能被17整除。例如,判斷1675282能不能被17整除,1675282的末三位是282,前面的數是1675,
282-1675×3=-4743,4743÷17=279,所以1675282能被17整除。
11、能被19整除的數的特征。
方法一:若一個整數的末三位與7倍的前面的隔出數的差能被19整除,則這個數能被19整除。例如,判斷234555能不能被19整除,234555末尾三位數是555,前面三位是234,
555-234×7=-1083,1083÷19=57,所以234555能被19整除。
方法二:若一個整數的個位數字截去,再從餘下的數中,加上個位數的2倍,如果和是19的倍數,則原數能被19整除。如果和太大或心算不易看出是否19的倍數,就需要繼續上述「截尾、倍大、相加、驗和」的過程,直到能清楚判斷為止。
12、能被23整除的數的特征。
若一個整數的末四位與前面5倍的隔出數的差能被23(或29)整除,則這個數能被23整除。
13、能被25整除的數的特征。
如果一個數的末尾兩位能被25整除,則這個數能被25整除。
14、能被125整除的數的特征。
如果一個數的末尾三位能被125整除,則這個數能被125整除。
分析2-為什麼將counter == 3判斷單獨拿出來就能求解了?
考慮將每個數字模3以後的結果。
如果對於當前數字能被3整除(0、3、6、9)模3結果為0的數,則直接個數加1
如果是兩個數字那就有四種可能(1,1) (2, 2) (1, 2) (2, 1)其中後兩個組合之和為3能被3整除
如果是三個數字對於之前兩個數字的組合只剩下(1, 1)和(2, 2) 那麼下個數不管是1還是2都可以組成一個3的整數倍
分析3-其他優質解法搜集:
解法一:
貪心思路:
對每位數字對3求餘,則結果只能是0、1、2.如果當前位是0,則對結果貢獻為1,如果不為0,則判斷連續出現2或者1的數目num,如果num%3為0,則對結果的貢獻為num/3,否則可以找到一個與當前數字不相等的數字(前面連續出現的是2,當前為1。或者前面連續出現的是1,當前為2),則對結果貢獻是num/3+1.
#include<bits/stdc++.h> using namespace std; string s; int main() { ios::sync_with_stdio(false), cin.tie(0); cin >> s; for(int i = 0; i < s.length(); i++) { s[i] = (s[i] - '0') % 3 + '0'; } int num = 1; int ans = 0; for(int i = 1; i < s.length(); i++) { if(s[i] == s[i-1]) num++; else { if(s[i] == '0') { ans += num / 3; num = 1; } else if(s[i-1] == '0') { ans += num; num = 1; } else { ans += num / 3; if(num % 3) { ans++; num = 0; } else num = 1; } } } if(s[s.length()-1] == '0') ans += num; else ans += num / 3; cout << ans << endl; return 0; }
解法二:
dp思路:
dp[i]表示截止到下標為i的元素之前最多有多少個片段%3=0。很容易想到當(sum[i]-sum[j]) % 3 == 0時,dp[i] = max{dp[j]} + 1;所以用一個pre[]數組表示和當前sum值相等的上一個sum值,中間肯定經歷了一個(+3)%3的過程。所以最終的狀態方程是dp[i] = max(dp[pre[sum]]+1, dp[i]);
#include<bits/stdc++.h> using namespace std; const int maxn = 1e7; string s; int dp[maxn], pre[maxn]; int main() { ios::sync_with_stdio(false), cin.tie(0); memset(pre, -1, sizeof(pre)); cin >> s; for(int i = 0; i < s.length(); i++) { s[i] = (s[i] - '0') % 3 + '0'; } dp[0] = (s[0] == '0'); int sum = s[0] - '0'; pre[sum] = 0; for(int i = 1; i < s.length(); i++) { int t = s[i] - '0'; sum = (sum + t) % 3; dp[i] = dp[i-1]; if(sum == 0) dp[i] = max(dp[i], 1); if(pre[sum] != -1) dp[i] = max(dp[pre[sum]] + 1, dp[i]); pre[sum] = i; } cout << dp[s.length()-1] << endl; return 0; }
解法三:大師兄的神奇迴圈解法:
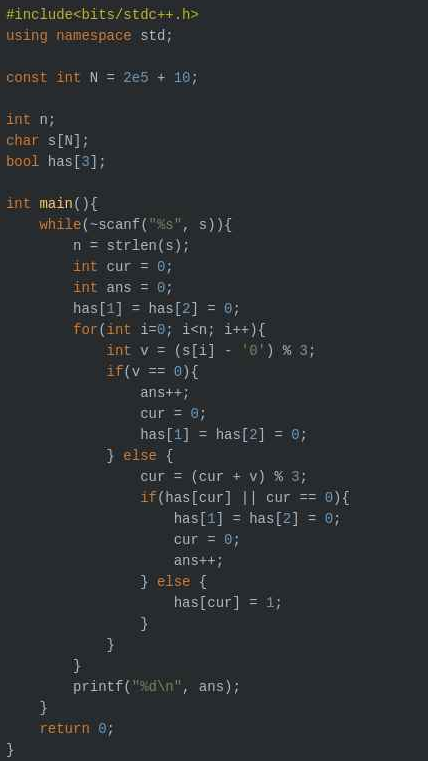
註:如果有更好的解法,真心希望您能夠評論留言貼上您的代碼呢~互相幫助互相鼓勵才能成長鴨~~



