冒泡排序---《程式員小灰》_ZenDei技術網路在線

————— 當天上午 ————— 什麼是冒泡排序？冒泡排序的英文Bubble Sort，是一種最基礎的交換排序。大家一定都喝過汽水，汽水中常常有許多小小的氣泡，嘩啦嘩啦飄到上面來。這是因為組成小氣泡的二氧化碳比水要輕，所以小氣泡可以一點一點向上浮動。而我們的冒泡排序之所以叫做冒泡排序，正是因為 ...

————— 當天上午 —————

什麼是冒泡排序？

冒泡排序的英文Bubble Sort，是一種最基礎的交換排序。

大家一定都喝過汽水，汽水中常常有許多小小的氣泡，嘩啦嘩啦飄到上面來。這是因為組成小氣泡的二氧化碳比水要輕，所以小氣泡可以一點一點向上浮動。

而我們的冒泡排序之所以叫做冒泡排序，正是因為這種排序演算法的每一個元素都可以像小氣泡一樣，根據自身大小，一點一點向著數組的一側移動。

具體如何來移動呢？讓我們來看一個慄子：

有8個數組成一個無序數列：5，8，6，3，9，2，1，7，希望從小到大排序。

按照冒泡排序的思想，我們要把相鄰的元素兩兩比較，根據大小來交換元素的位置，過程如下：

首先讓5和8比較，發現5比8要小，因此元素位置不變。

接下來讓8和6比較，發現8比6要大，所以8和6交換位置。

繼續讓8和3比較，發現8比3要大，所以8和3交換位置。

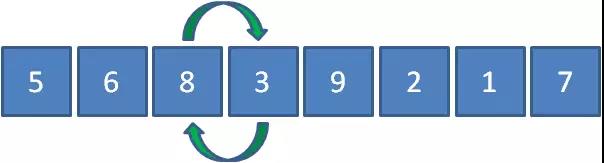
繼續讓8和9比較，發現8比9要小，所以元素位置不變。

接下來讓9和2比較，發現9比2要大，所以9和2交換位置。

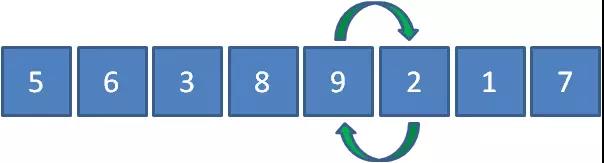
接下來讓9和1比較，發現9比1要大，所以9和1交換位置。

最後讓9和7比較，發現9比7要大，所以9和7交換位置。

這樣一來，元素9作為數列的最大元素，就像是汽水裡的小氣泡一樣漂啊漂，漂到了最右側。

這時候，我們的冒泡排序的第一輪結束了。數列最右側的元素9可以認為是一個有序區域，有序區域目前只有一個元素。

下麵，讓我們來進行第二輪排序：

首先讓5和6比較，發現5比6要小，因此元素位置不變。

接下來讓6和3比較，發現6比3要大，所以6和3交換位置。

繼續讓6和8比較，發現6比8要小，因此元素位置不變。

接下來讓8和2比較，發現8比2要大，所以8和2交換位置。

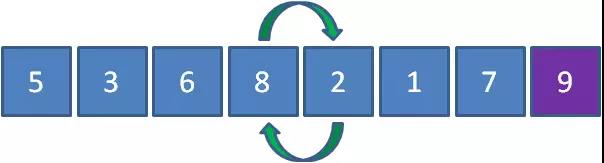
接下來讓8和1比較，發現8比1要大，所以8和1交換位置。

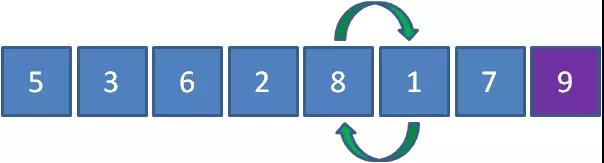
繼續讓8和7比較，發現8比7要大，所以8和7交換位置。

第二輪排序結束後，我們數列右側的有序區有了兩個元素，順序如下：

至於後續的交換細節，我們這裡就不詳細描述了，第三輪過後的狀態如下：

第四輪過後狀態如下：

第五輪過後狀態如下：

第六輪過後狀態如下：

第七輪過後狀態如下（已經是有序了，所以沒有改變）：

第八輪過後狀態如下（同樣沒有改變）：

到此為止，所有元素都是有序的了，這就是冒泡排序的整體思路。

原始的冒泡排序是穩定排序。由於該排序演算法的每一輪要遍歷所有元素，輪轉的次數和元素數量相當，所以時間複雜度是O（N^2） 。

冒泡排序第一版：

 1 public class BubbleSort {
 2 
 3     private static void sort(int array[]){
 4         int tmp  = 0;   
 5         for(int i = 0; i < array.length-1; i++){
 6             for(int j = 0; j < array.length - i - 1; j++){
 7                 if(array[j] > array[j+1]){
 8                     tmp = array[j];
 9                     array[j] = array[j+1];
10                     array[j+1] = tmp;
11                 }
12             }
13         }
14     }
15     public static void main(String[] args){
16         int[] array = new int[]{5,8,6,3,9,2,1,7};
17         sort(array);
18         System.out.println(Arrays.toString(array));
19      }
20 }

代碼非常簡單，使用雙迴圈來進行排序。外部迴圈控制所有的回合，內部迴圈代表每一輪的冒泡處理，先進行元素比較，再進行元素交換。

　　　　　　　　　　　　　　————————————

原始的冒泡排序有哪些優化點呢？

讓我們回顧一下剛纔描述的排序細節，仍然以5，8，6，3，9，2，1，7這個數列為例，當排序演算法分別執行到第六、第七、第八輪的時候，數列狀態如下：

很明顯可以看出，自從經過第六輪排序，整個數列已然是有序的了。可是我們的排序演算法仍然“兢兢業業”地繼續執行第七輪、第八輪。

這種情況下，如果我們能判斷出數列已經有序，並且做出標記，剩下的幾輪排序就可以不必執行，提早結束工作。

冒泡排序第二版

 1 public class BubbleSort {
 2 
 3     private static void sort(int array[]){
 4         int tmp  = 0;
 5         for(int i = 0; i < array.length-1; i++)    {
 6             //有序標記，每一輪的初始是true
 7             boolean isSorted = true;
 8             for(int j = 0; j < array.length - i - 1; j++) {
 9                 if(array[j] > array[j+1]){
10                     tmp = array[j];
11                     array[j] = array[j+1];
12                     array[j+1] = tmp;
13                     //有元素交換，所以不是有序，標記變為false
14                     isSorted = false;
15                 }
16             }
17             if(isSorted){
18                 break;
19             }
20         }
21     }
22     public static void main(String[] args){
23         int[] array = new int[]{5,8,6,3,9,2,1,7};
24         sort(array);
25         System.out.println(Arrays.toString(array));
26     }
27 }

這一版代碼做了小小的改動，利用布爾變數isSorted作為標記。如果在本輪排序中，元素有交換，則說明數列無序；如果沒有元素交換，說明數列已然有序，直接跳出大迴圈。

為了說明問題，咱們這次找一個新的數列：

這個數列的特點是前半部分（3，4，2，1）無序，後半部分（5，6，7，8）升序，並且後半部分的元素已經是數列最大值。

讓我們按照冒泡排序的思路來進行排序，看一看具體效果：

第一輪

元素3和4比較，發現3小於4，所以位置不變。

元素4和2比較，發現4大於2，所以4和2交換。

元素4和1比較，發現4大於1，所以4和1交換。

元素4和5比較，發現4小於5，所以位置不變。

元素5和6比較，發現5小於6，所以位置不變。

元素6和7比較，發現6小於7，所以位置不變。

元素7和8比較，發現7小於8，所以位置不變。

第一輪結束，數列有序區包含一個元素：

第二輪

元素3和2比較，發現3大於2，所以3和2交換。

元素3和1比較，發現3大於1，所以3和1交換。

元素3和4比較，發現3小於4，所以位置不變。

元素4和5比較，發現4小於5，所以位置不變。

元素5和6比較，發現5小於6，所以位置不變。

元素6和7比較，發現6小於7，所以位置不變。

元素7和8比較，發現7小於8，所以位置不變。

第二輪結束，數列有序區包含一個元素：

這個問題的關鍵點在哪裡呢？關鍵在於對數列有序區的界定。

按照現有的邏輯，有序區的長度和排序的輪數是相等的。比如第一輪排序過後的有序區長度是1，第二輪排序過後的有序區長度是2 ......

實際上，數列真正的有序區可能會大於這個長度，比如例子中僅僅第二輪，後面5個元素實際都已經屬於有序區。因此後面的許多次元素比較是沒有意義的。

如何避免這種情況呢？我們可以在每一輪排序的最後，記錄下最後一次元素交換的位置，那個位置也就是無序數列的邊界，再往後就是有序區了。

冒泡排序第三版

 1 public class BubbleSort {
 2 
 3     private static void sort(int array[]){
 4         int tmp  = 0;
 5         //記錄最後一次交換的位置
 6         int lastExchangeIndex = 0;
 7         //無序數列的邊界，每次比較只需要比到這裡為止
 8         int sortBorder = array.length - 1;
 9         for(int i = 0; i < array.length-1; i++){
10             //有序標記，每一輪的初始是true
11             boolean isSorted =true;
12             for(int j = 0; j < sortBorder; j++){
13                 if(array[j] > array[j+1]) {
14                 tmp = array[j];
15                 array[j] = array[j+1];
16                 array[j+1] = tmp;
17                 //有元素交換，所以不是有序，標記變為false
18                 isSorted = false;
19                 //把無序數列的邊界更新為最後一次交換元素的位置
20                 lastExchangeIndex = j;
21             }
22         }
23             sortBorder = lastExchangeIndex;
24             if(isSorted){
25                 break;
26             }
27         }
28     }
29 
30     public static void main(String[] args){
31        int[] array = new int[]{3,4,2,1,5,6,7,8};
32         sort(array);    
33         System.out.println(Arrays.toString(array));
34     }
35 }

這一版代碼中，sortBorder就是無序數列的邊界。每一輪排序過程中，sortBorder之後的元素就完全不需要比較了，肯定是有序的。